结构光三维重建之光栅图像相位解算(MATLAB)

1. 背景介绍

相位测量轮廓术（Phase Measurement Profilometry, PMP）基本思想是通过有一定相位差的多幅光栅条纹图像计算每个像素点的相位值，根据相位值计算物体的深度信息。对于双目视觉系统，由相位到深度计算的过程，可以是先进行相位匹配获取左右图像上的同名点，然后利用多片空间前方交会得到物体点三维坐标；也可以利用事先标定好的相位-深度对应关系直接获取深度信息。无论是哪种重建策略，首先是要根据相移的光栅图像计算得到每个像素点相位值。

图1 物体对条纹图像的相位调制
图2 双目PMP系统

2. 相位计算

假设条纹图像光强是标准正弦分布，则光强分布函数为$$I_i(x,y)=I^{\prime }(x,y)+I^{\prime \prime }(x,y)\cos ({\delta }_i+\varphi (x,y))$$其中，$I^{\prime }(x,y)$表示图像的平均灰度，当一个周期使用$n$步相移时，$I^{\prime }(x,y)=\frac{1}{n}{\sum }_{i=1}^n{I}_i(x,y)$，这一点证明就是将上式左右两边相加，余弦项在一个周期内积分为$0$；$I^{\prime \prime }(x,y)$为图像的灰度调制幅度；${\delta }_i$为图像的相位移；$\varphi (x,y)$为物体对光栅的调制的相对相位，也就是我们需要求解的值。标准$N$帧相移算法对系统的随机噪声具有抑制作用，是目前广泛使用的一种相移算法。

2.1 相位主值

采用标准的四步相移算法计算光栅图像的相位主值$\varphi (x,y)$，四幅光栅图像的相位移分别为：$0$, $\frac{\pi }{2}$,$\pi$,$\frac{3\pi }{2}$，由此光强分别为

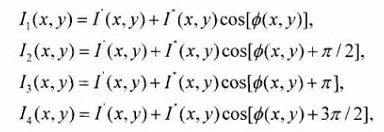
根据上述方程组求解相位主值为

通过以上四步相移方法计算相位主值$\varphi (x,y)$，从下图中可以看出虽然一个周期内相位从$0$到$2\pi$变换且唯一，但是在下一个周期又会出现相同的相位值。这样，不同位置的物体点不能唯一标识，因此，需要进行相位解包裹，或称为相位展开，目的就是让所有点能用相位来唯一的确定。

图3 四步相移的相位主值

2.2 相位解包裹

多频外差的相位解包裹方法，原理是将不同频率的两种相位函数${\varphi }_1(x,y)$，${\varphi }_2(x,y)$叠加以获取频率更低的相位函数${\varphi }_M(x,y)$。通过合理的选择频率值，使得叠加合成的波形在整个图像上只含有一个周期，一个周期内的相位是唯一的。

图4 相位展开

2.2.1 合成频率

如图5所示波叠加示意图，频率分别为$f_1$和$f_2$的余弦波叠加，根据三角函数和差化积公式

其合成的频率，即拍频，为频率之差【至于为什么不再除以2，以及为什么不是频率之和，等搞懂再补充更新】。$$f_{beat}=|f_2-f_1|$$若两个波的周期分别为${\lambda }_1$，${\lambda }_2$，则合成波的周期为$${\lambda }_{12}=\frac{{\lambda }_1{\lambda }_2}{{\lambda }_2-{\lambda }_1}$$

图5 两个频率不同的波叠加

将不同频率条纹进行叠加合成，目的就是如一开始相位展开所述，比如竖直条纹，其最终合成频率为图像的宽度。对于三频四步外差的相位展开，也就是三组不同频率的光栅图像，每一组是四步相移的图像，有多篇文献已经对三种频率的选择进行了讨论和研究。选取三个频率分别为70，64，59，对应周期分别为1/70，1/64，1/59。按照上述频率合成公式，第一组和第二组叠加${\lambda }_{12}=1/6$，第二组和第三组叠加${\lambda }_{23}=1/5$，最终这两组再叠加${\lambda }_{123}=1$，也就是在图像上最终合成的是一个周期。

2.2.2 合成相位

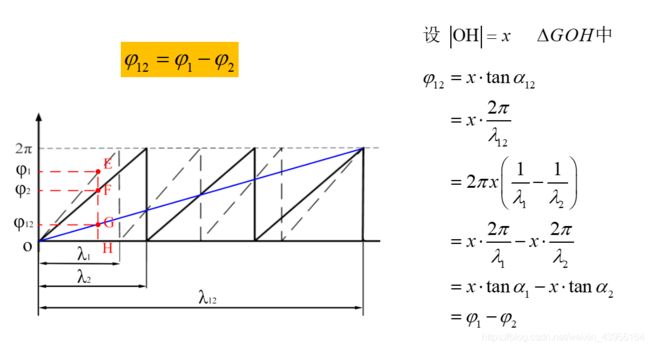
三频四步外差的相位展开，根据2.1四步相移得到三组频率的主相位分别为${\varphi }_1(x,y)$，${\varphi }_2(x,y)$，${\varphi }_3(x,y)$。两组不同频率的波叠加之后其合成相位为$${\varphi }_{12}(x,y)={\varphi }_1(x,y)-{\varphi }_2(x,y)$$证明如图6所示，周期为${\lambda }_1$，${\lambda }_2$叠加为周期为${\lambda }_{12}$，取H点出的相位分析，E、F对应H点处的主相位值为${\psi }_1$，${\psi }_2$，叠加波的相位为${\psi }_{12}={\psi }_1-{\psi }_2$。

图6 叠加相位证明

由此，根据第一组和第二组叠加${\varphi }_{12}(x,y)={\varphi }_1(x,y)-{\varphi }_2(x,y)$，第二组和第三组叠加${\varphi }_{23}(x,y)={\varphi }_2(x,y)-{\varphi }_3(x,y)$，最后将这两组再次叠加${\varphi }_{123}(x,y)={\varphi }_{12}(x,y)-{\varphi }_{23}(x,y)$。

2.2.3 相位展开

已经得到叠加频率、叠加相位，根据图4所示，需要将相位展开。选取第一组相位主值${\varphi }_1(x,y)$展开为$${\varphi }_M(x,y)={\varphi }_1(x,y)+int(\frac{{\varphi }_{123}(x,y)R-{\varphi }_1(x,y)}{2\pi })\cdot 2\pi$$其中，$int(\cdot )$代表向下取整，有的论文中使用的是$round(\cdot )$四舍五入【个人认为取四舍五入会造成展开的相位不是一直递增的，证明后补充更新】，R是一个常数$$R=\frac{\tan {\alpha }_1}{\tan {\alpha }_{123}}$$其中$$\tan {\alpha }_1=\frac{2\pi }{{\lambda }_1},\tan {\alpha }_{123}=\frac{2\pi }{{\lambda }_{123}}$$相位展开式证明如图7所示，蓝色为最终展开的相位，取x点处的相位进行分析。

图7 相位展开证明

3. Matlab代码

clc;close all;clear;
% 图像大小
width = 2448;  
height = 2048;
% 初始化3种频率，4步相移图像
I = zeros(height,width,12);
freq = [70 64 59]; 
% 导入图像，图像命名为Pic(1),Pic(2),...
for i=1:12
    number = num2str(i,'%d');
    filename = ['Pic(',number, ')','.bmp'];
    I(:,:,i) = double(imread(filename)) / 255.0;
end
% 相位主值
Phase = zeros(height,width,3);
for i = 1:3 % 每一组相同频率的有四张图片
     I1 = I(:,:,1 + (i-1)*4);
     I2 = I(:,:,2 + (i-1)*4);
     I3 = I(:,:,3 + (i-1)*4);
     I4 = I(:,:,4 + (i-1)*4); 
     Y = I4 - I2;
     X = I1 - I3;
     Phase(:,:,i) = atan2(Y, X);           
end
% 每一组的相位主值
PH1 = Phase(:,:,1);
PH2 = Phase(:,:,2);
PH3 = Phase(:,:,3);
figure(1),imshow(mat2gray(PH1));
figure(2),imshow(mat2gray(PH2));
figure(3),imshow(mat2gray(PH3));
% 叠加后相位主值
PH12 = zeros(height,width);
PH23 = zeros(height,width);
for i = 1:height
	for j = 1:width
		% 计算第一组和第二组的相差
		if PH1(i,j)>PH2(i,j)
			PH12(i,j) = PH1(i,j)-PH2(i,j);
		else
			PH12(i,j) = PH1(i,j)+2*pi-PH2(i,j);
		end
		% 计算第二组和第三组的相差
        if PH2(i,j)>PH3(i,j)
			PH23(i,j) = PH2(i,j)-PH3(i,j);
        else
			PH23(i,j) = PH2(i,j)+2*pi-PH3(i,j);
        end
	end
end
PH123 = zeros(height,width);
for i = 1:height
	for j = 1:width 
		if PH12(i,j)>PH23(i,j)
			PH123(i,j) = PH12(i,j)-PH23(i,j);
		else
			PH123(i,j) = PH12(i,j)+2*pi-PH23(i,j);
		end
	end
end
figure(4),imshow(mat2gray(PH12));
figure(5),imshow(mat2gray(PH23));
figure(6),imshow(mat2gray(PH123));
% 相位解包裹  相位展开
R = freq(1);
PH = PH1 + 2*pi*round((PH123*R - PH1)/(2*pi));
figure(7),imshow(mat2gray(PH));

参考文献

[1] 李中伟，基于数字光栅投影的结构光三维测量技术与系统研究[D]，华中科技大学，2009,05
[2] Reich C , Ritter R , Thesing J . White light heterodyne principle for 3D-measurement[C]// Sensors, Sensor Systems, and Sensor Data Processing. International Society for Optics and Photonics, 1997.
[3] Liu S , Feng W , Zhang Q , et al. Three-dimensional shape measurement of small object based on tri-frequency heterodyne method[C]// 2015 International Conference on Optical Instruments and Technology: Optoelectronic Measurement Technology and Systems. International Society for Optics and Photonics, 2015.
[4] Towers C E , Towers D P , Jones J D C . Absolute fringe order calculation using optimised multi-frequency selection in full-field profilometry[J]. Optics and Lasers in Engineering, 2005, 43(7):p.788-800.
[5] Reich, Carsten. 3-D shape measurement of complex objects by combining photogrammetry and fringe projection[J]. Optical Engineering, 2000, 39(1):224.