梯度下降求最小值和线性方程（线性回归详解）

线性回归

梯度下降法一般用于求解最小值，以下分别例举两种求最小值情况：
1）二次函数求最小值的情况
2）预测线性函数的情况（已知x和y，求解最合适的w和b，是预测误差最小）
以下就按照上述的两种情况进行分析。

1、二次函数求最小值的情况

1）首先导入包

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

2）定义二次函数与其导数方程，并画出函数图便于观察，也可以不画。

f = lambda x : x**2 -5*x + 10
g = lambda x : 2*x -5
x = np.linspace(-10,15,30)
plt.plot(x,f(x))

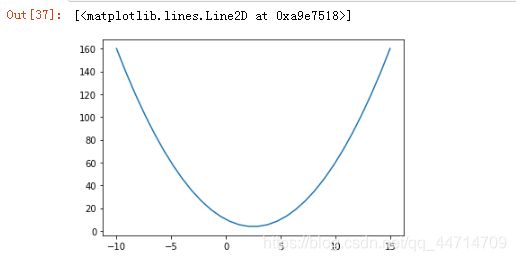
可以从图中观察或计算可得，最小值为2.5，用于与之后梯度下降求解到的最小值最对比。

3）开始使用梯度下降算法进行最小值求解

# 开始定义梯度下降算法
# 用于存放迭代结果，用于之后的可视化
result = []
# 随机初始化一个取最小值的x
v_ = np.random.randint(-10,10,size = 1)[0]
result.append(v_)
print('-----------随机初始化取最小值的x坐标',v_)
# 定义一个保存上一次迭代结果的变量
v_last = v_ + 1
# 设置结果的精准度
precision = 0.00001
# 设置最大迭代次数
max_count = 3000
# 迭代步幅
step = 0.1
count = 0
# 开始迭代
while True:
#     设置退出条件
    if np.abs(v_ - v_last) < precision:
        break
    if count > max_count:
        break
        
#     求更新上一次的值  
    v_last = v_
#     更新求解值
    v_ = v_ - g(v_)*step
    result.append(v_)
    print('-----------最小值的x坐标：%f'%v_,'迭代次数：%d'%count)
    count += 1

在上面的代码中要注意迭代时，是拿每一次的最小值进行迭代，而不是x，迭代结果如下：

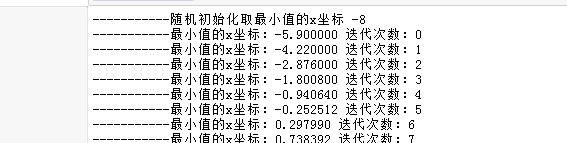
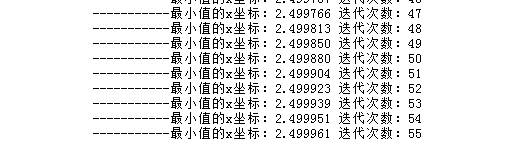
仅通过55次迭代，算法就找到了最小值的x坐标2.499961，注意：计算机找到的只都是无限接近我们要的结果，如果还想要更加准确的结果，可以增加准确精度的位数。

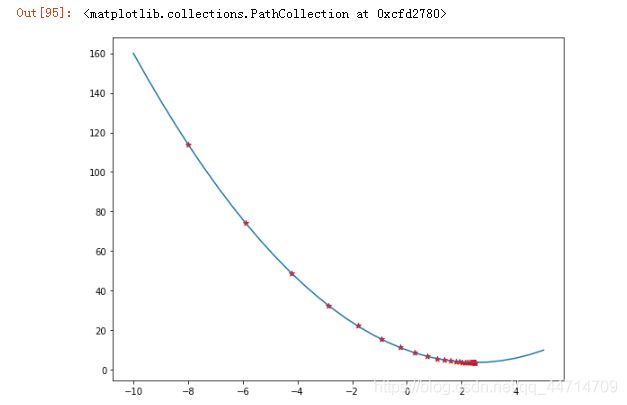
4）将刚才的迭代过程进行可视化

x = np.linspace(-10,5,30)
plt.figure(figsize=(9,7))
plt.plot(x,f(x))
plt.scatter(result,f(np.array(result)),marker='*',c = 'r')

2）预测线性函数的表达式

当已知x和y的时候，我们希望可以找到x和y之间的关系，以便于其他数据的预测，本文假设x与y之间是线性的。

1、还是先导包

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

2、手动生成具有线性关系的x和y

X = np.linspace(2,12,30)
w = np.random.randint(2,10,size = 1)[0]
b = np.random.randint(-5,5,size = 1)[0] 
y = X * w + b  + np.random.randn(30) * 2
# y = X * w + b 
plt.scatter(X,y)

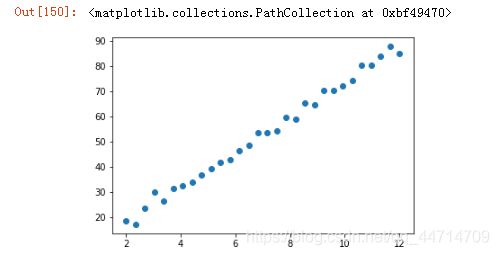
因为我们自己生成的数据，并且给出了w和b，因此是满足线性关系的，在显示的时候加入了扰动。下面的求解实在假设我们不知道w和b的条件下进行的，模仿sklearn中的线性回归包的方式，定义一个类来实现线性回归。

3）定义Lineaer_model类实现线性回归

class Linear_model:
#     初始化
    def __init__(self):
        self.w_ = np.random.randn(1)[0]
        self.b_ = np.random.randn(1)[0]
        print('------------随机初始化的w和b:',self.w_,self.b_)
    
#     定义模型的到预测的y
    def model(self,x):
        return  self.w_* x + self.b_
#     定义损失
    def loss(self,x,y):
#         误差通过最小二乘法来求
        cost= (y - self.model(x))**2
#         定义w和b的求取，通过求偏导
        d_w = 2*(y - self.model(x))*(-x)
        d_b = 2*(y - self.model(x))*(-1)
        return d_w,d_b
#   w和b的更新
    def gradient_decent(self,d_w,d_b,step=0.01):
        self.w_ = self.w_ - d_w*step
        self.b_ = self.b_ - d_b*step
        print('-------------迭代过程中的w_和b_:',self.w_,self.b_)
# 进行迭代        
    def fit(self,X,y):
#         定义一个d和w的更新值
        w_last = self.w_ + 1
        b_last = self.b_ + 1
#         设置准确精度
        precision = 0.00001
#         设置最大迭代次数
        max_count = 10000
        count = 0
        while True:
            if (np.abs(self.w_ - w_last) < precision) and (np.abs(self.b_ - b_last)<precision):
                break
            if count > max_count:
                break
            d_w = 0
            d_b = 0
            size = X.shape[0]
            for xi,yi in zip(X,y):
                d_w += self.loss(xi,yi)[0]/size
                d_b += self.loss(xi,yi)[1]/size
            self.gradient_decent(d_w,d_b)
            count +=1
            print('count:',count)
    def coef_(self):
        return self.w_
    def interrupt_(self):
        return self.b_

完成了上面的定义后，就可以调用，检验算法的准确性。

lm = Linear_model()
lm.fit(X,y)

迭代结果如下：



可以发现迭代后的结果是：w = 6.966，b = 3.94
而我们随机生成的w和b分别是7和4，结果还可以，如果不满意的话，还可以增加迭代次数。

4）调用sklearn的线性回归库，与自己写的算法作对比

from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(X.reshape(-1,1),y)
lr.coef_
lr.intercept_

结果如下：


可以发现我们算法求到的结果与直接导包求到的结果基本一致。