还不了解梯度下降法？看完这篇就懂了！

0x00 前言：机器学习方法论

在此之前，我们已经学习了分类算法：kNN算法，回归算法：线性回归。我们知道：

机器学习就是需找一种函数f(x)并进行优化， 且这种函数能够做预测、分类、生成等工作。

那么其实可以总结出关于“如何找到函数f(x)”的方法论。可以看作是机器学习的“三板斧”：

• 第一步：定义一个函数集合（define a function set）

• 第二步：判断函数的好坏（goodness of a function）

• 第三步：选择最好的函数（pick the best one）

我们先把目光放在第三步上：How to pick the best one ? 我们的目标是让损失函数最小化。这就引出了下面需要介绍的方法：梯度下降是目前机器学习、深度学习解决最优化问题的算法中，最核心、应用最广的方法。

0x01 为什么需要梯度下降算法

如果我们抛开具体场景，仅从数学抽象的角度来看：每个模型都有自己的损失函数，不管是监督式学习还是非监督式学习。损失函数包含了若干个位置的模型参数，比如在多元线性回归中，损失函数：   ，其中向量 表示未知的模型参数，我们就是要找到使损失函数尽可能小的参数未知模型参数。

在学习简单线性回归时，我们使用最小二乘法来求损失函数的最小值，但是这只是一个特例。在绝大多数的情况下，损失函数是很复杂的（比如逻辑回归），根本无法得到参数估计值的表达式。因此需要一种对大多数函数都适用的方法。这就引出了“梯度算法”。

我们先了解一下梯度下降是用来做什么的?

首先梯度下降(Gradient Descent, GD)，不是一个机器学习算法，而是一种基于搜索的最优化方法。梯度下降(Gradient Descent, GD)优化算法，其作用是用来对原始模型的损失函数进行优化，以便寻找到最优的参数，使得损失函数的值最小。

要找到使损失函数最小化的参数，如果纯粹靠试错搜索，比如随机选择1000个值，依次作为某个参数的值，得到1000个损失值，选择其中那个让损失值最小的值，作为最优的参数值，那这样太笨了。我们需要更聪明的算法，从损失值出发，去更新参数，且要大幅降低计算次数。

梯度下降算法作为一个聪明很多的算法，抓住了参数与损失值之间的导数，也就是能够计算梯度（gradient），通过导数告诉我们此时此刻某参数应该朝什么方向，以怎样的速度运动，能安全高效降低损失值，朝最小损失值靠拢。

0x02 什么是梯度

简单地来说，多元函数的导数(derivative)就是梯度(gradient)，分别对每个变量进行微分，然后用逗号分割开，梯度是用括号包括起来，说明梯度其实一个向量，我们说损失函数L的梯度为：

我们知道导数就是变化率。梯度是向量，和参数维度一样。

假设，我们有一个二元函数 。那么f的梯度为：

例如在点(1,2)，梯度∇f的取值为：

那么这个梯度有什么用呢？

在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率 在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向

梯度指向误差值增加最快的方向，导数为0（梯度为0向量）的点，就是优化问题的解。在上面的二元函数中，点(1,2)向着(4,2)的方向就是梯度方向 为了找到这个解，我们沿着梯度的反方向进行线性搜索，从而减少误差值。每次搜索的步长为某个特定的数值 ，直到梯度与0向量非常接近为止。更新的点是 所有点的x梯度， 所有点的y梯度

0x03 理解梯度下降算法

很多求解最优化问题的方法，大多源自于模拟生活中的某个过程。比如模拟生物繁殖，得到遗传算法。模拟钢铁冶炼的冷却过程，得到退火算法。其实梯度下降算法就是模拟滚动，或者下山，在数学上可以通过函数的导数来达到这个模拟的效果。

梯度下降算法是一种思想，没有严格的定义。

3.1 场景假设

梯度下降就是从群山中山顶找一条最短的路走到山谷最低的地方。

既然是选择一个方向下山，那么这个方向怎么选？每次该怎么走？选方向在算法中是以随机方式给出的，这也是造成有时候走不到真正最低点的原因。如果选定了方向，以后每走一步，都是选择最陡的方向，直到最低点。

总结起来就一句话：随机选择一个方向，然后每次迈步都选择最陡的方向，直到这个方向上能达到的最低点。

梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景：

一个人被困在山上，需要从山顶到山谷。但此时雾很大，看不清下山的路径。他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，随机选择一个方向，然后每次迈步都选择最陡的方向。然后每走一段距离，都反复采用同一个方法：如果发现脚下的路是下坡，就顺着最陡的方向走一步，如果发现脚下的路是上坡，就逆着方向走一步，最后就能成功的抵达山谷。

3.2 数学推导

从数学的角度出发，针对损失函数L，假设选取的初始点为 ；现在将这个点稍微移动一点点，得到 。那么根据泰勒展开式（多元函数的一阶展开式）：

设我们移动的“一点点”为  ，则我们可以得到 ，将泰勒展开式代入其中，我们则得到：

如果我们令移动的距离分别为：  ，其中规定 ，则可以得到：

这就说明，我们如果按照规定的移动距离公式移动参数，那么损失函数的函数值始终是下降的，这样就达到了我们要求的“损失变小”的要求了。如果一直重复这种移动，则可以证明损失函数最终能够达到一个最小值。

那么我们就可以得到损失函数值（也就是下一步的落脚点）的迭代公式：

针对于上述公式，有一些常见的问题：

为什么要梯度要乘以一个负号？

我们已经知道：梯度的方向就是损失函数值在此点上升最快的方向，是损失增大的区域，而我们要使损失最小，因此就要逆着梯度方向走，自然就是负的梯度的方向，所以此处需要加上负号

关于参数  :

我们已经知道，梯度对应的是下山的方向，而参数  对应的是步伐的长度。在学术上，我们称之为“学习率”(learning rate)，是模型训练时的一个很重要的超参数，能直接影响算法的正确性和效率：

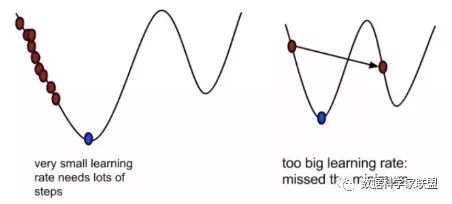
• 首先，学习率 不能太大。因此从数学角度上来说，一阶泰勒公式只是一个近似的公式，只有在学习率很小，也就是 很小时才成立。并且从直观上来说，如果学习率 太大，那么有可能会“迈过”最低点，从而发生“摇摆”的现象（不收敛），无法得到最低点

• 其次，学习率 又不能太小。如果太小，会导致每次迭代时，参数几乎不变化，收敛学习速度变慢，使得算法的效率降低，需要很长时间才能达到最低点。

3.3 致命问题

梯度算法有一个比较致命的问题：

从理论上，它只能保证达到局部最低点，而非全局最低点。在很多复杂函数中有很多极小值点，我们使用梯度下降法只能得到局部最优解，而不能得到全局最优解。那么对应的解决方案如下：首先随机产生多个初始参数集，即多组 ；然后分别对每个初始参数集使用梯度下降法，直到函数值收敛于某个值；最后从这些值中找出最小值，这个找到的最小值被当作函数的最小值。当然这种方式不一定能找到全局最优解，但是起码能找到较好的。

对于梯度下降来说，初始点的位置，也是一个超参数。

0xFF 总结

在机器学习的“三板斧”中，第三步的目标是让损失函数最小化，从而引出了梯度下降法，这一目前机器学习、深度学习解决最优化问题的算法中，最核心、应用最广的方法。所谓梯度下降，是一种基于搜索的最优化方法，其作用是用来对原始模型的损失函数进行优化，找到使损失函数（局部）最小的参数。

首先对梯度下降有一个整体的印象：梯度是向量，是多元函数的导数，指向误差值增加最快的方向。我们沿着梯度的反方向进行线性搜索，从而减少误差值，是为梯度下降。然后我们通过“下山”这样的模拟场景，以及严谨的数据公式推导深刻理解了梯度下降算法，并引出了学习率的概念。最后我们给出了梯度下降方法的不足和改进方法。

相信大家看完本篇文章后，对梯度下降算法一定有了一个更加深刻的认识。如果没懂？那就再多看几遍吧（笑）