吴恩达机器学习ex5 python实现

正则化线性回归

这一部分，我们需要先对一个水库的流出水量以及水库水位进行正则化线性归回。然后将会探讨方差-偏差的问题

数据可视化

import numpy as np
import pandas as pd
import scipy.io as sio
import scipy.optimize as opt
import matplotlib.pyplot as plt
import seaborn as sns

data = sio.loadmat('ex5data1.mat')
X,y,Xval,yval,Xtest,ytest = map(np.ravel,[data['X'],data['y'],data['Xval'],data['yval'],data['Xtest'],data['ytest']])
X.shape,y.shape,Xval.shape,yval.shape,Xtest.shape,ytest.shape

((12,), (12,), (21,), (21,), (21,), (21,))

fig,ax = plt.subplots(figsize=(12,8))
ax.scatter(X,y)
ax.set_xlabel('water level')
ax.set_ylabel('flow')
plt.show()

正则化线性回归代价函数

theta初始值为[1,1]，输出应该为303.993

# 把各个X项中都加入常数项1
X, Xval, Xtest = [np.insert(x.reshape(x.shape[0], 1), 0, np.ones(x.shape[0]), axis=1) for x in (X, Xval, Xtest)]

def cost(theta,X,y):
    m = X.shape[0]
    error = X@theta - y
    J = error.T@error/(2*m)
    return J

# X是m*n维，m个样本，n个特征
# y是m维，theta是n维
def costReg(theta,X,y,learning_rate):
    m = X.shape[0]
    error = X@theta - y #R(m*1)
    reg = (learning_rate/(2*m)) * np.power(theta[1:],2).sum() 
    
    J = error.T@error/(2*m)
    J += reg
    
    return J

theta = np.ones(X.shape[1]) #初始化为1
learning_rate = 1
costReg(theta,X,y,learning_rate)

303.9931922202643

正则化线性回归梯度

设定初始值为[1,1]，输出应该为[-15.30, 598.250]

def gradientReg(theta,X,y,learning_rate):
    m = X.shape[0]
    
    grad = X.T @ (X@theta-y) #(m,n).T @ (m,1) -> (n,1)
    grad /= m
    
    reg = theta.copy() #根据公式只需要更改常数项的theta即可
    reg[0] = 0
    reg = (learning_rate/m) * reg
    grad += reg
    
    return grad 

gradientReg(theta,X,y,learning_rate)

array([-15.30301567, 598.25074417])

线性回归可视化

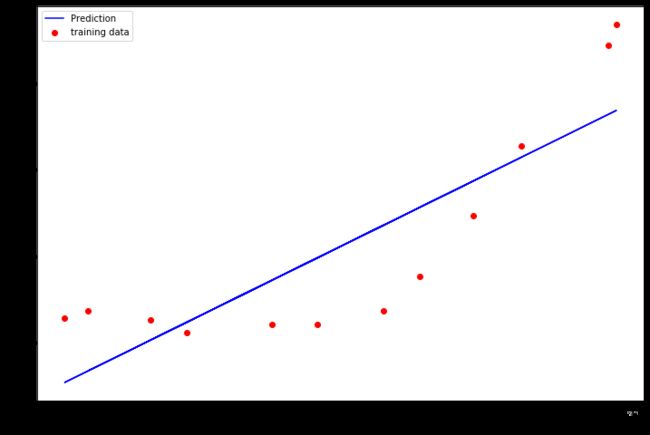
调用工具库找到最优解，在这个部分，我们令$\lambda =0$。因为我们现在训练的是2维的，所以正则化不会对这种低维的有很大的帮助。
完成之后，将数据和拟合曲线可视化。

theta = np.ones(X.shape[1])
final_theta = opt.minimize(fun = costReg,x0=theta,args=(X,y,0),method='TNC',jac=gradientReg,options={'disp':True}).x
final_theta

array([13.08790362,  0.36777923])

b = final_theta[0]
m = final_theta[1]

fig,ax = plt.subplots(figsize=(12,8))
plt.scatter(X[:,1],y,c='r',label='training data')
plt.plot(X[:,1],X[:,1]*m+b,c='b',label='Prediction')
ax.set_xlabel('water level')
ax.set_ylabel('flow')
ax.legend()
plt.show()

方差和偏差

机器学习中的一个重要概念是偏差-方差权衡。偏差较大的模型会欠拟合，而方差较大的模型会过拟合。这部分会让你画出学习曲线来判断方差和偏差的问题。

学习曲线

1.使用训练集的子集来拟合模型

2.在计算训练代价和验证集代价时，不用正则化

3.使用相同的训练集子集来计算训练代价

#X是特征矩阵，(m.n+1)维（多了常数项的1）
#y是目标向量 m维， learning_rate是正则化系数
def linear_regression(X,y,learning_rate):
    #初始化参数
    theta = np.ones(X.shape[1])
    res = opt.minimize(fun=costReg,x0=theta,args=(X,y,learning_rate),method='TNC',jac = gradientReg,options={'disp':True})
    return res

training_cost,cv_cost=[],[]

m = X.shape[0]
for i in range(1,m+1):
    res = linear_regression(X[:i,:],y[:i],0)
    
    tc = cost(res.x,X[:i,:],y[:i])
    cv = cost(res.x,Xval,yval)
    
    training_cost.append(tc)
    cv_cost.append(cv)

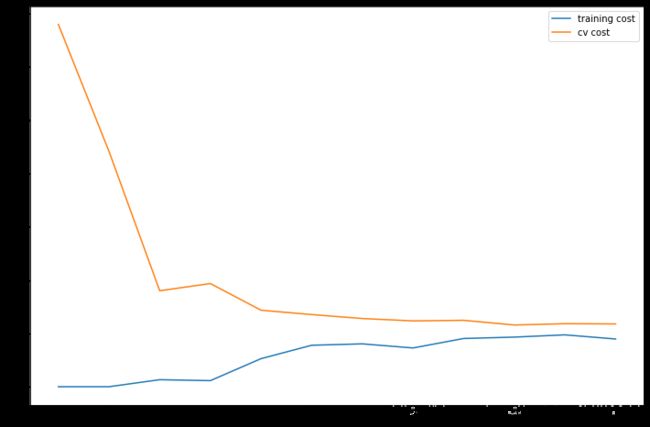
fig,ax = plt.subplots(figsize=(12,8))
plt.plot(np.arange(1,m+1),training_cost,label='training cost')
plt.plot(np.arange(1,m+1),cv_cost,label='cv cost')
plt.legend()
plt.show()
#典型的欠拟合，高偏差（bias）

多项式回归

线性回归对于现有数据来说太简单了，会欠拟合，我们需要多添加一些特征。
写一个函数，输入原始X，和幂的次数p，返回X的1到p次幂

def poly_features(x,power,as_ndarray=False):
    data = {'f{}'.format(i):np.power(x,i) for i in range(1,power+1)}
    df = pd.DataFrame(data)
    
    return df.values if as_ndarray else df

data = sio.loadmat('ex5data1.mat')
X,y,Xval,yval,Xtest,ytest = map(np.ravel,[data['X'],data['y'],data['Xval'],data['yval'],data['Xtest'],data['ytest']])

poly_features(X,3)

	f1	f2	f3
0	-15.936758	253.980260	-4047.621971
1	-29.152979	849.896197	-24777.006175
2	36.189549	1309.683430	47396.852168
3	37.492187	1405.664111	52701.422173
4	-48.058829	2309.651088	-110999.127750
5	-8.941458	79.949670	-714.866612
6	15.307793	234.328523	3587.052500
7	-34.706266	1204.524887	-41804.560890
8	1.389154	1.929750	2.680720
9	-44.383760	1969.918139	-87432.373590
10	7.013502	49.189211	344.988637
11	22.762749	518.142738	11794.353058

多项式回归

1.使用之前的代价函数和梯度函数
2.扩展特征到8阶特征
3.使用归一化来处理$x^n$
4.$\lambda =0$

def normalize_features(df):
    """对所有的样本进行归一化"""
    return df.apply(lambda column:(column - column.mean())/column.std())

def prepare(x,power):
    df = poly_features(x,power=power)
    ndarr = normalize_features(df).values
    return np.insert(ndarr,0,np.ones(ndarr.shape[0]),axis=1)

def prepare_poly_data(*args,power):
    """持续寻找X，Xval和Xtest"""
    return [prepare(x,power) for x in args]

X_poly,Xval_poly,Xtest_poly = prepare_poly_data(X,Xval,Xtest,power = 8)
X_poly[:3,:]

array([[ 1.00000000e+00, -3.62140776e-01, -7.55086688e-01,
         1.82225876e-01, -7.06189908e-01,  3.06617917e-01,
        -5.90877673e-01,  3.44515797e-01, -5.08481165e-01],
       [ 1.00000000e+00, -8.03204845e-01,  1.25825266e-03,
        -2.47936991e-01, -3.27023420e-01,  9.33963187e-02,
        -4.35817606e-01,  2.55416116e-01, -4.48912493e-01],
       [ 1.00000000e+00,  1.37746700e+00,  5.84826715e-01,
         1.24976856e+00,  2.45311974e-01,  9.78359696e-01,
        -1.21556976e-02,  7.56568484e-01, -1.70352114e-01]])

画出学习曲线，因为没有使用正则化所以 $\lambda =0$

def plot_learning_curve(X,Xinit,y,Xval,yval,learning_rate=0):
    training_cost,cv_cost=[],[]
    m = X.shape[0]
    
    for i in range(1,m+1):
        #对前i项进行线性回归，计算出theta
        res = linear_regression(X[:i,:],y[:i],learning_rate=learning_rate)
        
        #这里计算代价的时候不需要用正则化代价函数，因为正则化只是用来适配参数的
        tc = cost(res.x,X[:i,:],y[:i])
        cv = cost(res.x,Xval,yval)
        
        training_cost.append(tc)
        cv_cost.append(cv)
        
    fig,ax = plt.subplots(2,1,figsize=(12,12))
    ax[0].plot(np.arange(1,m+1),training_cost,label='training cost')
    ax[0].plot(np.arange(1,m+1),cv_cost,label='cv cost')
    ax[0].legend()
    
    fitx = np.linspace(-50,50,100)
    fitxtmp = prepare_poly_data(fitx,power = 8)
    fity = np.dot(prepare_poly_data(fitx,power=8)[0],linear_regression(X,y,learning_rate).x.T)
    
    ax[1].plot(fitx,fity,c='r',label='fitcurve')
    ax[1].scatter(Xinit,y,c='b',label='initial_Xy')
    ax[1].set_xlabel('water_level')
    ax[1].set_ylabel('flow')
    

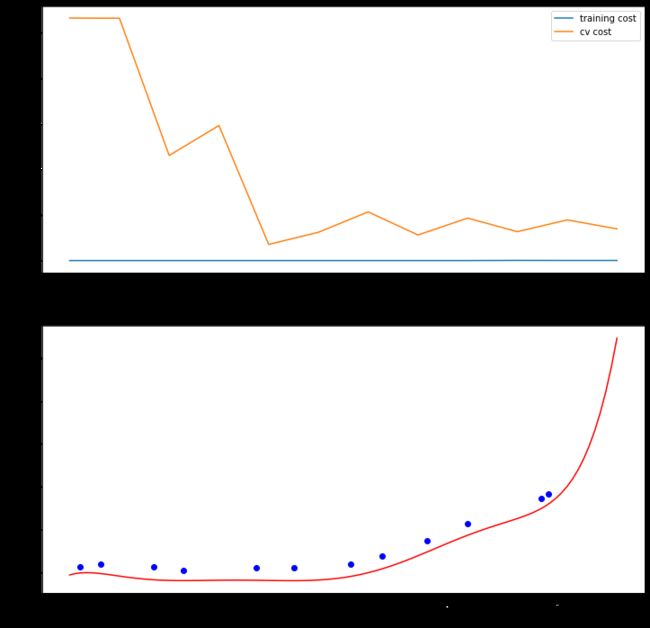
plot_learning_curve(X_poly,X,y,Xval_poly,yval,learning_rate=0)
plt.show()
#训练的代价太低了，所以是过拟合

调整正则化系数$\lambda$

令$\lambda =1$

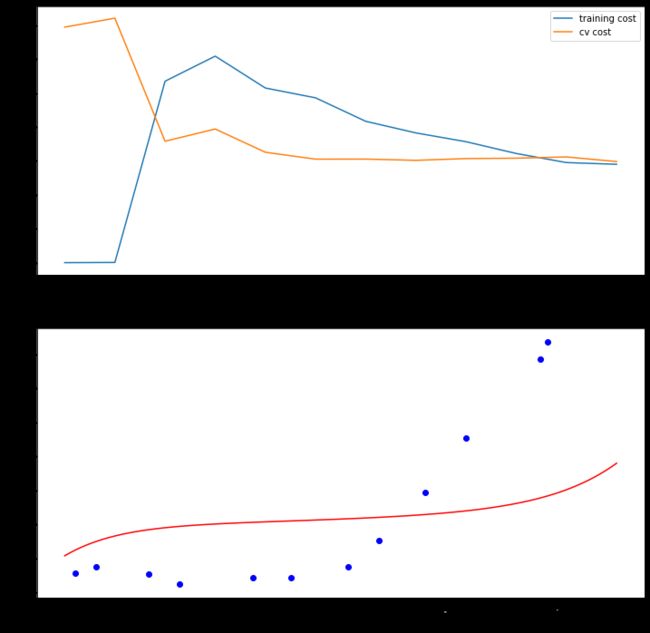
plot_learning_curve(X_poly, X, y, Xval_poly, yval, learning_rate=1)
plt.show()
#依然过拟合，但是我们看到代价不是0，所以有所改变了

令$\lambda =100$

plot_learning_curve(X_poly, X, y, Xval_poly, yval, learning_rate=100)
plt.show()
#可以看出训练代价和验证代价都非常大，说明我们在高误差的情况下，再加上观察回归曲线，我们现在欠拟合

找到最佳的$\lambda$

通过之前的实验，我们可以发现$\lambda$可以极大程度地影响正则化多项式回归。
所以这部分我们会会使用验证集去评价$\lambda$的表现好坏，然后选择表现最好的$\lambda$后，用测试集测试模型在没有出现过的数据上会表现多好。
尝试$\lambda$值[0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]

learning_rate_candidate=[0,0.001,0.003,0.01,0.003,0.1,0.3,1,3,10]
training_cost,cv_cost = [],[]

for learning_rate in learning_rate_candidate:
    res = linear_regression(X_poly,y,learning_rate)
    
    tc = cost(res.x,X_poly,y)
    cv = cost(res.x,Xval_poly,yval)
    
    training_cost.append(tc)
    cv_cost.append(cv)

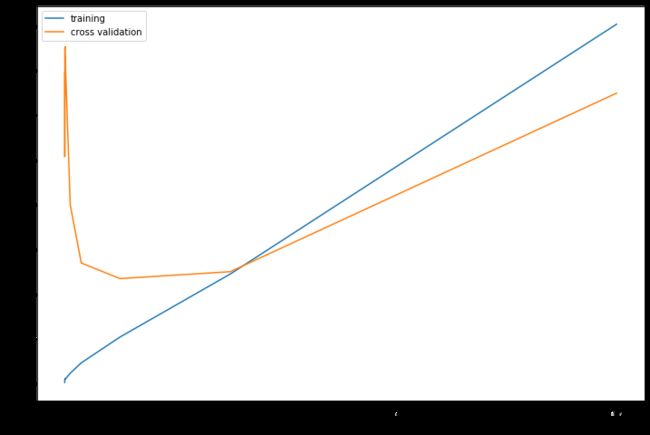
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(learning_rate_candidate, training_cost, label='training')
ax.plot(learning_rate_candidate, cv_cost, label='cross validation')
plt.legend()
plt.xlabel('lambda')
plt.ylabel('cost')
plt.show()
#当lambda为1的时候，cost最小

计算测试集上的误差

实际上，为了获得一个更好的模型，我们需要把最终的模型用在一个从来没有在计算中出现过的测试集上，也就是说，需要既没有被用作选择$\theta$，也没有被用作选择$\lambda$的数据

for learning_rate in learning_rate_candidate:
    theta = linear_regression(X_poly,y,learning_rate).x
    print('test cost(l={})={}'.format(learning_rate,cost(theta,Xtest_poly,ytest)))

test cost(l=0)=9.982275423899827
test cost(l=0.001)=10.96403493885111
test cost(l=0.003)=11.264458872657682
test cost(l=0.01)=10.880094765571297
test cost(l=0.003)=11.264458872657682
test cost(l=0.1)=8.632063139750382
test cost(l=0.3)=7.336640278544401
test cost(l=1)=7.466289435179381
test cost(l=3)=11.64393193727906
test cost(l=10)=27.715080291767972

可以看出来当$\lambda =0.3$的时候，代价最小，大约为7.33，和上图未调参的情况有所不同