数字信号处理FIR滤波器实验

目录

一、题目介绍以及函数准备

二、程序源代码以及图像 

 三、思考 为何线性相位是一个来回往返的折线形？

---

一、题目介绍以及函数准备

要求设计一个线性相位FIR数字低通滤波器来对模拟信号进行滤波，

技术要求为fp=4kHz，fst=4.5kHz，

As=60dB，抽样频率fs=20kHz。

选择合适的窗函数及窗长度，求h(n)并画出幅度响应曲线（dB）及相位响应曲线。

ceil函数：向上取矩阵元素的整数值，等价于

 freqz_m函数：

[db,mag,pha,grd,w] = freqz_m(b,a);

db = [0 到pi弧度]区间内的相对振幅(db)

mag = [0 到pi弧度]区间内的绝对振幅

pha = [0 到pi弧度]区间内的相位响应

grd = [0 到pi弧度]区间内的群迟延

w = [0 到pi弧度]区间内的501个频率样本向量

b = Ha(z)的分子多项式系数(对FIR b=h)

a = Ha(z)的分母多项式系数(对 FIR: a=[1])

这里可以多加一句，为何b=h;

因为

所以.

此处LATEX代码也很有趣

\begin{split}
&\because H(z)  =  \frac{Y(z)}{X(z)}  =  \sum_{k  =  0}^{M} b_{k}z^{-k}\\
&\therefore h(n)= \sum_{k  =  0}^{M} b_{k}\delta (n-k)
\end{split}

fir1函数：Window-based FIR filter design

本题的用法是h=fir1(M,wn,blackman(N));

M=N-1；wn — 截止频率， 0≤wn≤1。

二、程序源代码以及图像 

%习题8.7
% 要求设计一个线性相位FIR数字低通滤波器来对模拟信号进行滤波，
% 技术要求为fp=4kHz，fst=4.5kHz，
% As=60dB，抽样频率fs=20kHz。
% 选择合适的窗函数及窗长度，求h(n)并画出幅度响应曲线（dB）及相位响应曲线。


clear all;
clc;

Fs=20*10^3;fp=4000;fst=4500;
wp=2*pi*fp/Fs;ws=2*pi*fst/Fs;Rp=0.5; As=60;
wc=(wp+ws)/2;       %截止频率
wn=wc/pi;
deltaw=ws-wp;
N=ceil(11*pi/deltaw);M=N-1;             %求阶次N, 将 X 的每个元素四舍五入到大于或等于该元素的最接近整数
%N=220,表明需要取220个点才能满足阻带最小衰减的条件
n=[0:N-1];
h=fir1(M,wn,blackman(N));%wn — 截止频率， 0≤wn≤1 M  — 滤波器阶数 得到加了N阶Blackman窗函数之后的h(n)响应
%w = blackman(L) returns an L-point symmetric Blackman window.
[db,mag,pha,grd,w]=freqz_m(h,[1]);      %具体实现见7.6题解答过程
% [db,mag,pha,grd,w] = freqz_m(b,a);
%     db = [0 到pi弧度]区间内的相对振幅(db)
%    mag = [0 到pi弧度]区间内的绝对振幅
%    pha = [0 到pi弧度]区间内的相位响应
%    grd = [0 到pi弧度]区间内的群迟延
%      w =  [0 到pi弧度]区间内的501个频率样本向量
%      b = Ha(z)的分子多项式系数(对FIR b=h)
%      a = Ha(z)的分母多项式系数(对 FIR: a=[1])
dw=2*pi/1000;

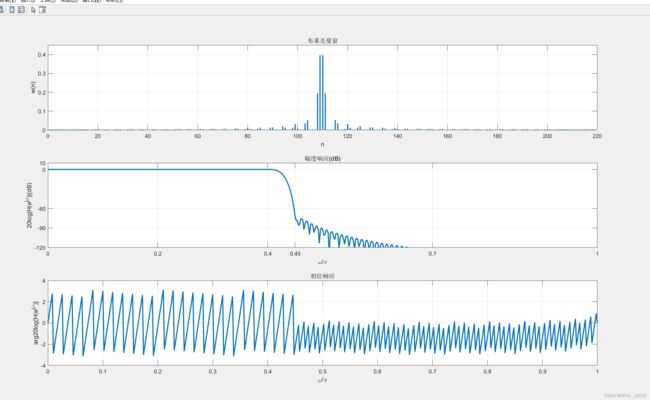
subplot(311)        %作图
stem(n,h,'.','linewidth',2); title('布莱克曼窗');xlabel('n'); ylabel('w(n)');axis([0,N,0,0.45]);grid

subplot(312)
plot(w/pi,db,'linewidth',2); 
title('幅度响应(dB)');xlabel('\omega/\pi'); ylabel('20log|H(e^j^\omega)|(dB)');axis([0,1,-120,10]);grid
set(gca,'xtickmode','manual','xtick',[0,0.2,0.4,0.45,0.7,1.0]);%人为设置坐标点
set(gca,'ytickmode','manual','ytick',[-120,-90,-60,0,10]);

subplot(313)
plot(w/pi,pha,'linewidth',2); axis([0,1,-4,4]);grid
title('相位响应');xlabel('\omega/\pi'); ylabel('arg20log[H(e^j^\omega)]');
%%
% w = blackman(10);
% stem([1:10],w);

 

 三、思考 为何线性相位是一个来回往返的折线形？

未完待续......