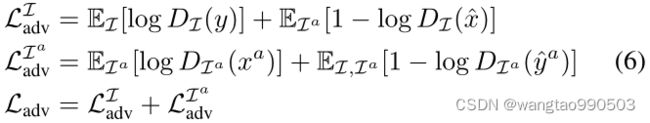ADN: Artifact Disentanglement Network forUnsupervised Metal Artifact Reduction--无监督的CT重建
本文提出了第一个无监督的金属伪影去除方法，具体地说，它引入了一种新的伪影解缠网络，该网络将金属伪影从潜伏空间的CT图像中解缠。它支持不同形式的生成(伪影减少、伪影转移和自我重建等)。该模型实现了比现有的监督模型等效的结果，并且比它们的泛化能力更强。
介绍
成对的带有金属伪影和不带有金属伪影的图像在实际中是很难获取的，于是大多数的监督方法都是求助于人工合成的带有伪影的图像来进行训练，然而，由于金属伪影的复杂性和CT设备的变化，合成的伪影可能无法准确地再现真实的临床场景，并且这些监督方法的性能在临床应用中往往会下降。
图1. 伪影解缠：输入带伪影的x^a和干净的y，通过内容空间的变化对x进行解缠，解缠得到的伪影图像再与y组合生成带伪影的y^a，具体用法看后文
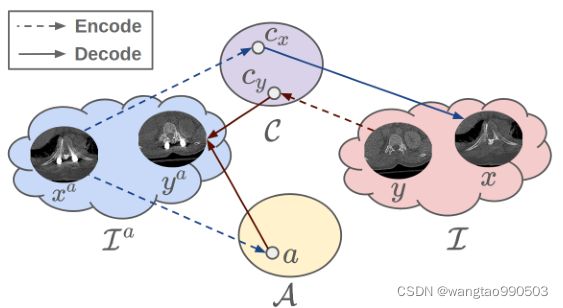
本文将伪影减少问题重新表述成伪影解缠问题，如图1所示，我们假设任何受伪像影响的图像都由伪像成分(即，金属伪像、噪声等)和内容成分(即无伪影图像)。我们的目标是在潜在空间中解开这两个分量，并且通过重建没有伪影分量的ct图像可以容易地实现伪影的减少。基本上，通过将ct图像分组为两组，一组具有金属伪影，另一组没有金属伪影，使得这种没有成对图像的伪影解开成为可能。
提出了一种具有专门编码器和解码器的伪像解缠绕网络(ADN ),这些编码器和解码器分别处理非配对输入的伪像和内容分量的编码和解码。
相关工作
这部分作者分为三个部分描述了前人的工作和他们的不足之处，分别是传统去噪方法，深度去噪方法和无监督图像翻译，最后提出了自己方法相比以前的主要贡献：
1. 包括了更多关于伪影解缠的动机和假设的细节，以帮助读者更好地理解这一工作
2. 更新了相关符号和公式，更精确的描述这项工作
3. 讨论了损失函数和网络体系结构的设计选择的原因，以更好地告知和启发读者我们的工作。
4. 添加了几个实验来更好地证明所提出的方法的有效性。
5. 对这项工作的意义和潜在应用的讨论。
PS：感觉都是空话。。。因为这篇论文实际上是翻修版本，他的真实贡献可能在前一篇里面，但是这并不妨碍我们对后续内容的理解。
方法
设
是所有受伪影影响的ct图像的域，
是所有无伪影的CT图像的域。我们将![P = [ (x^{a}, x) | x^{a} \in I^{a}, x \in I, f(x^{a}) \in x ]](http://img.e-com-net.com/image/info8/c7d90f5a63a34e85b82366bf9d13d71a.gif){kind=small}
表示为一组成对的图像，其中f : → 是从
中去除金属伪影的MAR模型。在这项工作中，我们假设没有这样的成对数据集可用，我们建议使用不成对的图像来学习
。
如图1所示，所提出的方法通过将受伪影影响的图像
的伪影分量和内容分量分别编码到内容空间 
和伪影空间 
中来解开它们。如果很好地解决了解缠问题，则编码的内容分量
∈ 应该不包含关于伪影的信息，同时保留所有的内容信息。因此，从解码应该给出无伪像的图像，它是
的消除伪像的对应物。另一方面，也可以将无伪影图像 
编码到给出内容代码 
的内容空间中。如果 与伪像码
一起被解码，我们获得受伪像影响的图像
。在接下来的章节中，我们将介绍一种无需配对数据就能学习这些编码和解码的伪影解缠结网络(ADN)。
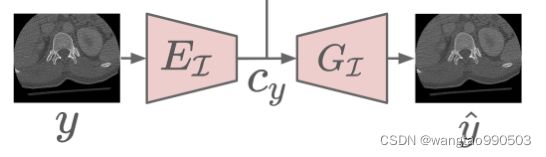
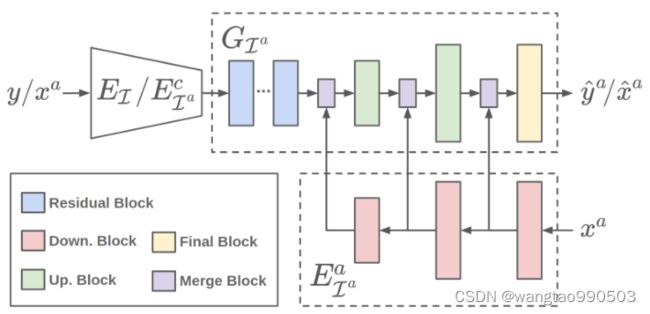
A. Encoders and Decoders
ADN的架构如图2所示。它包含一对无伪影的图像编码器
: 
和解码器
: 
以及一对受伪影影响的图像编码器
和解码器
。
编码器将图像样本从图像域映射到潜在空间，解码器将潜在代码从潜在空间映射回图像域。注意，与传统编码器不同，
由内容编码器
和伪像编码器
组成，它们分别对内容和伪像进行编码，以实现伪像的消除。
为了让读者能看到后面的几个公式，我们先举个例子，而后列出模型的公式表示：
给定两个不成对的图像 ∈ 和 ∈ ，和分别将和的内容分量映射到内容空间
。将的伪像分量映射到伪像空间。
公式如下：
和 分别表示含金属伪影的图像和不含金属伪影的图像，表示将含金属伪影的图像编码至内容域C，EaIa表示将含金属伪影的图像编码至伪影域A，表示将不含金属伪影的图像编码至内容域C。
公式2：第一个式子表示利用的内容信息和伪影信息
重新生成图像；第二个式子表示利用的内容信息和的伪影信息重新生成图像。
上述表示重新对仅含解剖结构的信息（不含伪影信息）重新进行解码，得到不含金属伪影的图像。
上述表示将含有金属伪影的图像 
编码至C空间，并进行重建。
B. Learning
对于ADN来说，学习一个MAR模型 : → 意味着学习和这两个关键组件。仅对受伪像影响的图像的内容进行编码，GI使用编码的内容代码生成无伪像的图像。因此，它们的组合很容易导致MAR模型， = 
。然而，在没有配对数据的情况下，直接解决这两个组件的学习是具有挑战性的。因此，我们在ADN中学习和以及其他编码器和解码器。这样，可以利用不同的学习信号来调整和的训练，并消除对成对数据的需求。
图3. 损失函数间的关系
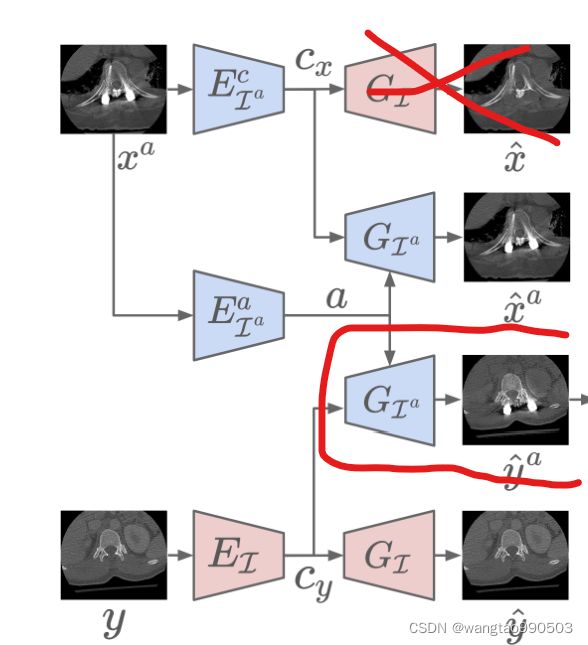
学习的目的是鼓励编码器和解码器的输出，以实现伪影的消除。也就是说，我们设计损失函数，使得ADN输出预期图像，如等式2-4所示。损失函数和ADN输出之间关系的概述如图3所示。我们可以观察到，ADN实现了五种形式的损失，即两种对抗性损失
和
、伪影一致性损失
、重建损失Lrec和自缩减损失
。总目标函数被公式化为这些损失的加权和，
后面的内容是对loss进行说明，也可以说是对ADN的架构运作方式进行说明，文中的说法比较复杂，这里我描述一下自己的想法，供读者进行思考：
如上图，根据初始输入的数据，这两对输入输出是可以被训练的，这俩很明显类似于自编码器的样子。
根据上面两个部件的训练，图中被红线框起来的部分应该是可得到的。因为
经过训练。
最后根据这一部分得出我们最关心的
PS：仅供参考，也希望各位读者可以批评指正
Adversarial Loss（对抗性损失）
通过解缠伪影分量，ADN输出
（公式3）和（公式2）其中前者从中移除伪像，而后者将伪像添加到y中。学习生成这两个输出对于伪像消除的成功至关重要。然而，由于没有成对的图像，不可能简单地应用回归损失，例如L1或L2损失，来最小化ADN输出和NDCT之间的差异。为了解决这个问题，我们采用了对抗学习的思想，通过引入两个鉴别器
和
来调整和的似然性。
一方面，/学会区分图像是由ADN生成的还是从/真实采样的，另一方面，ADN学会欺骗和，使它们无法确定来自ADN的输出是生成图像还是真实图像。这样，，ADN都可以不用成对图像进行训练。形式上，对抗性损失可以写成：
Reconstruction Loss（重建损失）
总结下来就一句话：ADN要求{EIa，GIa}和{EI，GI}在对同一图像进行编码和解码时充当自动编码器，我们使用L1损耗而不是L2损耗来鼓励更清晰的输出。：
Artifact Consistency Loss（伪影一致性损失）
对抗损失通过鼓励与来自I的样本相似来减少金属伪影。但是以这种方式获得的仅在解剖学上是合理的，而不是解剖学上精确的，即可能在解剖学上不对应于。（人话就是：生成的结果符合计算机审美但不符合人类的审美，参考WGAN引入VGG损失的原因）ADN通过引入伪影一致性损失来解决解剖精确性问题：
这种损失是基于这样的观察，和之间的差异以及和y之间的差异应该是接近的，因为使用了相同的伪像。与直接最小化和之间的差异不同，只要求和在解剖学上接近，但不完全接近，对于和 亦然。
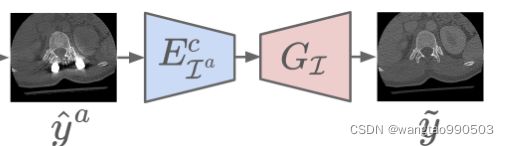
Self-Reduction Loss（自减少损失）
ADN还引入了自还原机制。它首先将工件添加到中，从而创建出，然后从中移除工件，从而生成
。因此，我们可以将与配对，通过回归来调整伪影减少：
C. Network Architectures
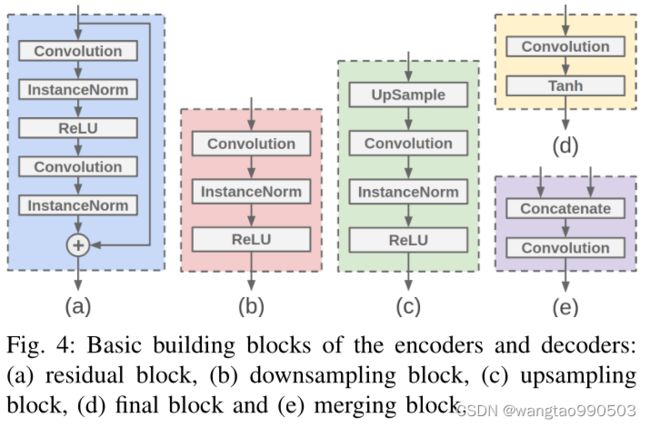
作者将构建组件，即编码器、解码器和鉴别器，公式化为卷积神经网络(CNN)。表1列出了它们的详细架构。
如图4所示，有五种不同类型的块。残差、下采样和上采样模块是编码器和解码器的核心模块。下采样块(图4b)使用步长卷积来降低特征图的维数，与最大池化图层相比，步长卷积自适应地选择用于缩减采样的要素，这为生成型模型提供了更好的性能。而上采样层采用了最邻近插值，而不是反卷积以避免棋盘伪影。编码器和解码器的块中所有卷积层的填充都是反射填充。它沿生成图像的边缘提供了更好的结果。
图4.
提出了一种特殊的方法：在进行解码以生成受伪像影响的图像过程中合并伪像代码和内容代码。参考特征金字塔网络(FPN) ，作者将这种设计称为伪像金字塔解码(APD)。对于伪影编码和解码，我们的目标是有效地恢复伪影的细节。图5展示了APD的详细架构。由几个下采样块组成，输出不同比例的特征图，即特征金字塔。由一堆残差、合并、上采样和最终块组成。它通过在解码期间合并不同尺度的伪影代码来生成受伪影影响的图像。中的合并块(图4e)首先沿着channel 维度连接内容特征图和伪影特征图，然后使用1 × 1卷积来合并特征（压缩通道）。
实验和结果
该部分在此不进行赘述，感兴趣的读者可以下载原文查阅，此文仅记录参数设置。
该文章在一个合成数据集和两个临床数据集上评估了所提出的方法，分别将它们称为SYN、CL1和CL2。对于SYN数据，从DeepDescence中随机选择4118个无伪影的CT图像，并按照CNNMAR中的方法合成金属伪影。对于CL1和CL2数据集，分别将它们分为两组，即含金属伪影和不含金属伪影。
使用具有
学习率的Adam优化器来最小化目标函数。对于超参数，我们对SYN和CL1（数据集）使用
，
，对CL2（数据集）使用，
。