小波变换(wavelet transform)
Chapter1 什么是小波?
小波变换跟时间有关,横坐标是时间,纵坐标是频率。
真实世界的数据或者信号经常表现出缓慢变化的趋势或因瞬态而出现的震荡,另一方面,图像具有被边缘中断或者对比度突然变化的平滑区域,傅里叶变换不能有效代表突然的变化,这是因为傅里叶变换将数据表示为未在时间或空间上定位的正弦波之和,这些正弦波永远震荡。
为了很好准确分析突然变化的信号和图像,我们需要使用在时间和频率上都很好定位的一类新功能,就是小波变换。
小波变换是快速衰减的波,例如震荡,均值为0,小波存在有限的持续时间。
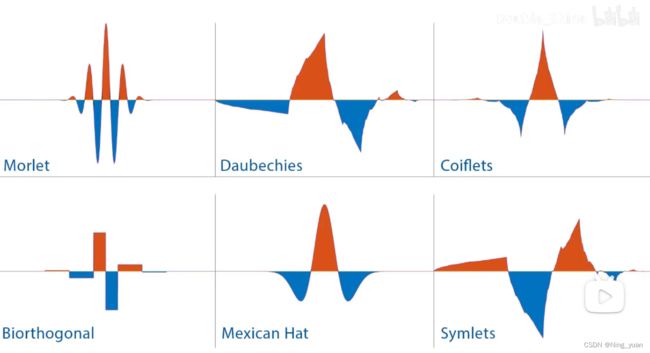
一些知名的小波形状:
多种小波的可用性是小波分析的关键优势。
下面介绍两个重要的小波变换概念:
1.缩放(scaling)
假设信号完整性(si)为t,缩放比例是指及时拉伸或收缩信号的过程,可以用等式表示:
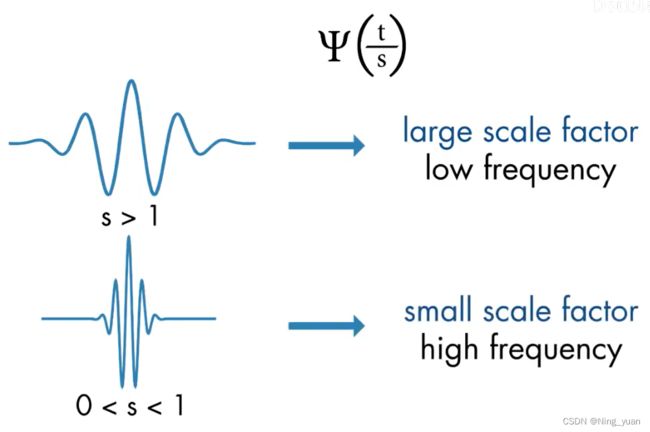
s是一个缩放系数,它是正值,对应于信号在时间上缩放了多少。比例因子与频率成反比
例如,将正弦波按比例缩放两个会导致其原始频率降低一半(或八度,八度就是一半的频率)
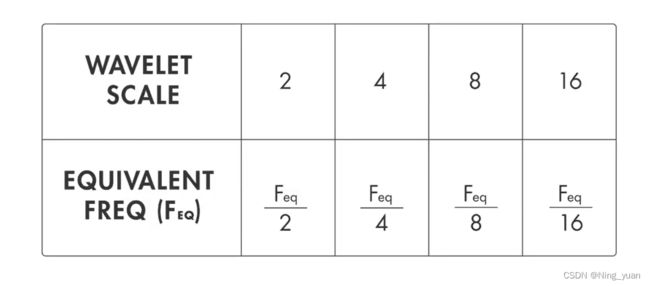
对于小波,比例和频率之间存在比例关系恒定的倒数关系,这个比例常数称为小波的中心频率。(center frequency)。这是因为与正弦波不同,小波在频率中具有带通特性(只允许某一段频率通过)。在数学上,等效频率使用以下公式定义: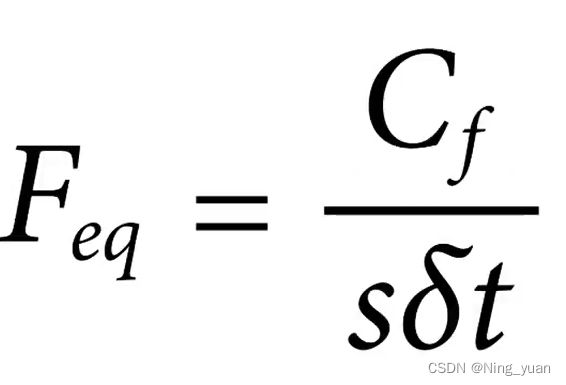
其中Cf是小波of的中心频率,是小波刻度,delta t 是采样间隔,因此将小波缩放2倍时,它会导致等效频率降低八度。
中心频率:通常定义为带通滤波器(或带阻滤波器)频率的几何平均值,在对数坐标下,即为两个3dB点之间的中点,一般用两个3dB点的算术平均来表示。滤波器通频带中间的频率,以中心频率为准,高于中心频率一直到频率电压衰减到0.707倍时为上边频,相反为下边频,上边频和下边频之间为通频带。
合成器中使用的滤波器通常有四种形式:低通、高通、带通、陷波。顾名思义低通就是让低频通过,滤掉高频;高通是让高频通过,滤掉低频;带通是让某一个范围的频率通过,滤除其余频率;陷波是滤除某一个范围的频率,让其余频率通过。
有几个常用的名词也顺便在这里介绍一下:被滤波器阻挡的频率范围称为禁带(Stopband);能顺利通过滤波器的频率范围称为通带(Passband);禁带的开始处称作半功率点(Half-power point)。滤波器允许或阻止一定的频率通过并不象刀切一样突然变化,而是有一个过渡,是一条斜线。斜线的倾斜程度用斜率(Slop)来表示。当输出信号下降3分贝时,就是半功率点,也叫负3分贝点,大家可能更加熟悉它的另一个称呼“截止频率”(Cutoff Frequency)。合成器中滤波器的截止频率经常是可以随便移动的。带通和陷波滤波器各自有两个半功率点,这两点的中心称为中心频率(Center Frequency)。
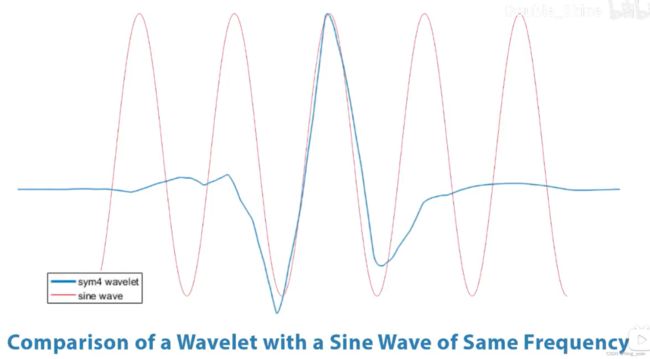
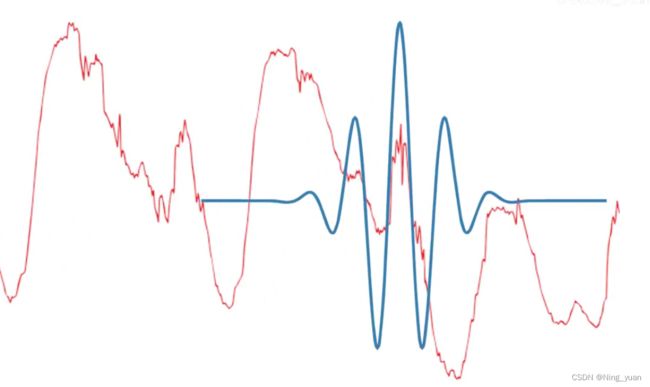
这是中心频率为0.07赫兹的小波的[sim]与相同频率的正弦波对应的方式
较大的比例因子会导致拉伸的小波,对应于较低的频率,反之。
拉伸小波有助于捕获信号中缓慢变化的变化,压缩的小波有助于捕捉突变。
可以构建与先前提到的等效频率成反比的不同比例
2.移位(shifting)
移动小波只是意味着沿信号长度延迟或推进小波的开始,以 表示的移位小波意味着小波被移位并以k为中心。我们需要移动小波使其与信号中寻找的特征对齐。
表示的移位小波意味着小波被移位并以k为中心。我们需要移动小波使其与信号中寻找的特征对齐。
小波分析中两个主要的变换是连续和离散小波变换,这些变换基于小波的缩放和移动方式而有所不同。
Chapter2 小波变换的类型
1.连续小波变换(CWT)
连续小波变换的关键应用是时频分析和时域频率成分滤波。
你可以使用此变换获得信号的同时时频分析,解析小波最适合时频分析,因为这些小波不具有负频率分量。
CWT的输出是系数,它是比例(scale)或频率和时间的函数。
现在讨论构造不同小波尺度的过程:
使用CWT,您可以在每个八度音阶中的中间尺度上分析信号时增强灵活性,此参数称为八度音阶的音阶数,每个八度音阶的音阶数越多,音阶离散化越好。
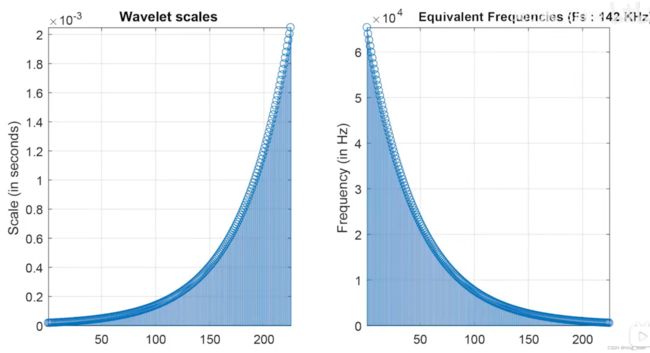
此参数的典型值为10,12,16,32,比例乘以信号的采样间隔以获得物理意义。
左边是一个凹凸小波的音阶示例,每个八度音阶有32个音阶,每7微秒对信号进行一次采样,右边是比例尺等效频率的对应图。实际比例值是指数的。
现在每个尺度小波在整个信号长度上随时间移动,并与原始信号进行比较,对所有比例尺重复此过程,得到的系数是小波比例尺和位移参数的函数。一个具有1000个样本的信号(以20个标度进行分析),会得出20000个系数。
这样,您可以通过连续小波变换更好地表征信号中的振荡行为
2.离散小波变换(DWT)
离散小波分析的关键应用是信号和图像的去噪和压缩
因为它有助于表示许多自然产生的信号和具有较少系数的图像,这样就可以表示稀疏。
DWT中的基本比例设置为2,通过将此基本比例提升为以下图1这种方式表示的整数值,可以获得不同比例。平移以该方程式表示的整数倍发生,此过程通常称为二进位缩放和平移(dyadic scaling and shifting)。这种采样消除了系数的冗余,变换地输出产生与输入信号长度相同数量的系数,因此需要更少内存。
离散小波变换过程等效于将信号与离散多速率滤波器组进行比较。总概念上讲,给定信号s,首先使用特殊的低通和高通滤波器对信号进行滤波,以产生低通和高通子带,将它们称为a1和d1,根据奈奎斯特准则,过滤后丢弃一半样本,滤波器通常具有少量系数,并具有良好的计算性能,这些滤波器还具有重构子带的能力,同时消除下采样而引起的任何混叠。对于下一级的分解,低通子带a1通过相同技术进行迭代滤波,以产生较窄的子带a2和d2,以此类推。
每个子带的系数长度是前一级系数数的一半。通过这种方式,DWT有助于以不同的分辨率分析逐渐变窄的子带上的信号,有助于去噪和压缩信号。
Chapter3 离散小波变换的一个应用示例
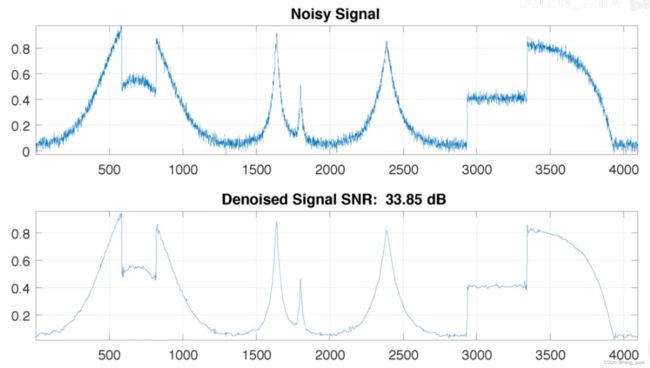
下图是增加的噪声的信号,我们使用离散小波变换对噪声信号进行去噪。
步骤:
1.获得近似系数和细节系数:通过执行多级小波分解来做到。
离散小波变换将信号分成低通子带,也称为近似水平,高通子带也称为细节等级,你可以分解多个级别或比例的近似子带,以进行精细比例分析。
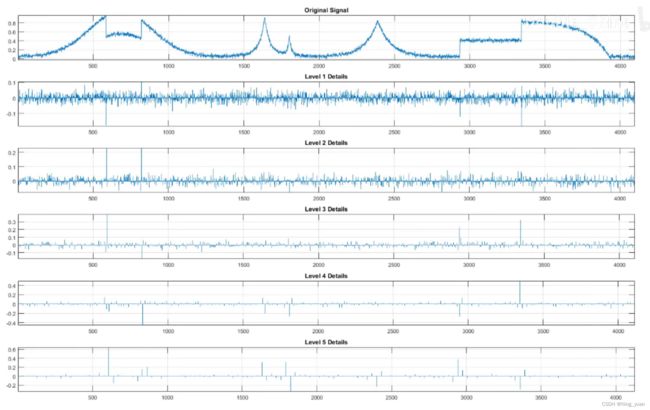
我们将使用相同的六个小波并将噪声信号分为五个级别,函数输出第五级逼近函数和一到五级细节函数。
第一级细节系数捕获信号的高频,大部分高频成分由信号中的噪声组成,但是高频的一部分是由信号的突然变化组成的,有时候这些突然的变化带有意义,您可能希望在消除噪声的同时保留此信息。
这里是原始信号以及1至5级绘制的细节,注意随着规模或级别的增加,详细信息中的活动急剧减少,因此我们暂时先专注于1级细节,忽略其他。
我们的目标是在消除噪音的同时保留急剧变化,一种方法是通过细节系数按阈值缩放。
2.分析细节并确定合适的阈值技术
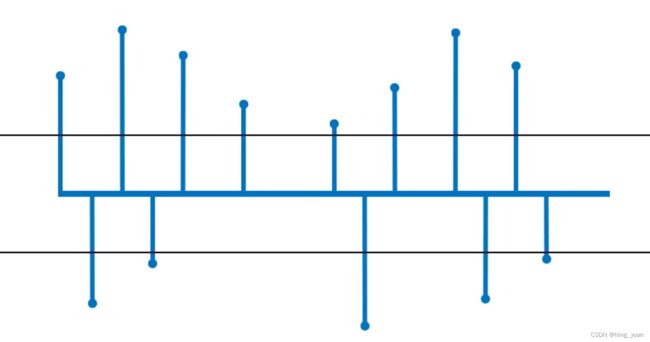
两种阈值操作:软阈值和硬阈值。在这两种情况下,幅度小于阈值的系数都设置为0,这两种阈值技术的区别在于如何处理幅度大于阈值的系数。
在软阈值的情况下,通过从系数值中减去阈值,将幅度大于阈值的系数缩小为0。
而在硬阈值中,幅度大于阈值的系数保持不变
3.设置细节系数阈值并重建信号
下图为去噪后的结果
性能比较:小波变换去噪最好,虽然看起来滑动平均去噪效果更好但是丢失了很多突变信号,所以信噪比(SNR)变小了。
Chapter4 连续小波变换的一个应用示例
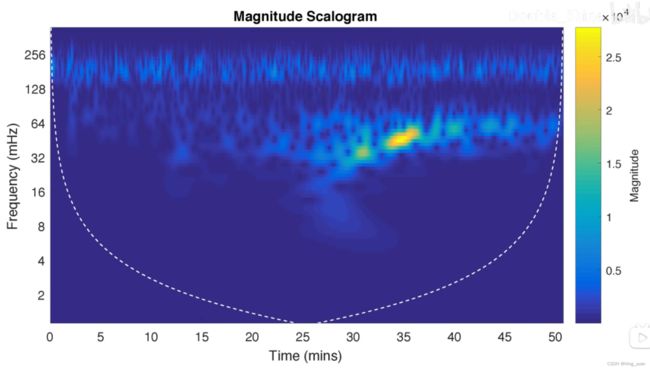
可以看到将噪声与地震信号分离是多么困难!!!许多自然信号都有这样的特征,它们由缓慢的变化组成,并散布着突然变化,通常被掩埋在噪音中,小波在分析这类信号非常有用!!!
采用傅里叶变换来产生时频可视化,可以看到两个地震活动实例无法区分。
我们看到的只是一个信号分布在0.05赫兹附近,但定位不完全.让我们尝试通过减少频谱图中使用的窗口大小来本地化事件时会发生什么。通过减小窗口的大小,我们可以在30和33分钟左右看到一些亮点,但两个事件并没有很好的分开,事件的频率和事件不确定仍然很高,减小窗口大小不是很有帮助。
我们需要以某种方式定位这两个事件的频率信息,这次使用小波。使用连续小波变换有助于获得地震数据的联合时频分析,未指定小波默认使用Moore小波。CWT函数根据小波能量散布自动确定分析的最小和最大尺度,函数返回的小波系数大小用颜色编码,白色虚线表示影响锥,在该区域内小波系数估计是可靠的。我们可以看到两次活动明显分开,这两个事件在时间和频率上都很好定位了。