数据挖掘课程笔记--分类(5)人工神经网络
一、神经元模型
“神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应”[Kohonen,1988]
神经网络中最基本的成分是神经元模型。在生物神经网络中,每个神经元与其他神经元相连,当它“兴奋”时,就会向相连的神经元发送化学物质,从而改变这些神经元内的电位;如果某神经元的电位超过了一个“阈值”(threshold), 那么它就会被激活,即“兴奋”起来,向其他神经元发送化学物质。
1943年, McCulloch and Pitts将上述情形抽象为下图所示的简单。模型,这就是一直沿用至今的“M-P神经元模型”。在这个模型中,神经元接收到来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,然后通过激活函数处理,产生神经元的输出。
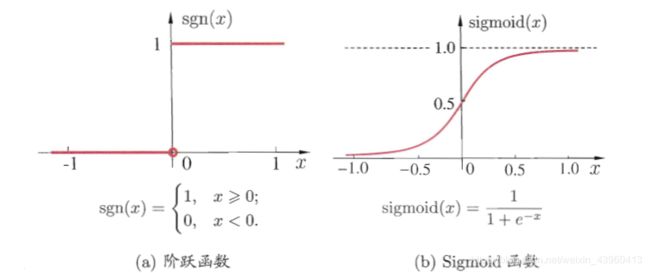
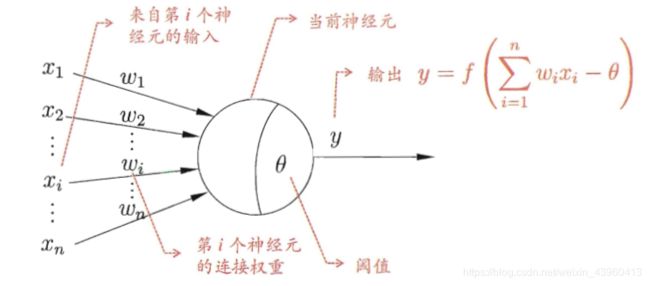 理想中的激活函数为阶跃函数,将输入值映射为“0”或“1”,其中“1”为神经元兴奋,“0”为抑制。由于阶跃函数具有不连续、不光滑等性质,常用Sigmoid函数作为激活函数。它把可能在较大范围内变化的输入值挤压到(0,1)的输出范围内,故也称为挤压函数。
理想中的激活函数为阶跃函数,将输入值映射为“0”或“1”,其中“1”为神经元兴奋,“0”为抑制。由于阶跃函数具有不连续、不光滑等性质,常用Sigmoid函数作为激活函数。它把可能在较大范围内变化的输入值挤压到(0,1)的输出范围内,故也称为挤压函数。
 把许多个这样的神经元按一定层次结构连接起来,就得到了神经网络
把许多个这样的神经元按一定层次结构连接起来,就得到了神经网络
二、感知机
感知机包含两种结点:几个输入结点,用来表示输入属性;一个输出结点,用来提供模型输出。神经网络结构中的结点通常叫作神经元或单元。
在感知机中,每个输入结点都通过一个加权的链连接到输出结点。这个加权的链用来模拟神经元间神经键连接的强度。像生物神经系统一样,训练一个感知机模型就相当于不断调整链的权值,直到能拟合训练数据的输入输出关系为止。
感知机能容易地实现逻辑与或非运算。假设f为阶跃函数,
![]()
“与”(x1^x2):令w1=w2=1,Θ=2,则y=f(1x1+1x2-2),仅在x1=x2=1时,y=1;
“或”(x1∨x2):令w1=w2=1,Θ=0.5,则y=f(1x1+1x2-0.5),仅在x1=1或x2=1时,y=1;
“非”(x1┐x2):令w1=-0.6,w2=0,Θ=-0.5,则y=f(-0.6x1+0x2+0.5),当x1=1,y=0;当x1=0时,y=1;
例:使用感知机模拟一个布尔函数:
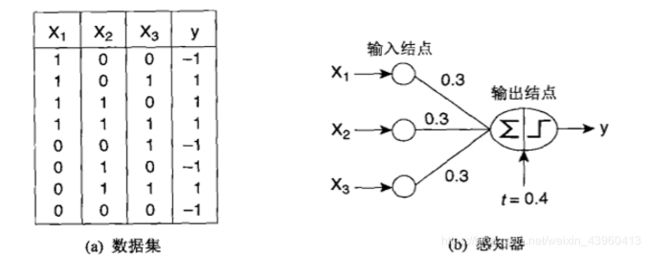
感知机对输入加权求和,再减去偏置因子t,然后考察结果的符号,得到输出值y。上图中的模型有三个输入结点,各结点到输出结点的权值都等于0.3,偏置因子t = 0.4。模型的输出计算公式如下:
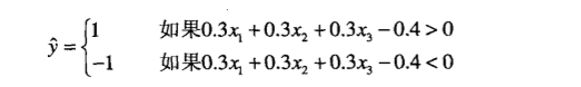
例如,如果x=1,xz=1,x=0,那么y=+1,因为0.3x1+0.3x2+0.3x-0.4是正的。
如果x=0,x2=1, x3=0,那么y=-1,因为加权和减去偏置因子值为负。
三、多层人工神经网络-BP算法
多层人工神经网络比单层感知机的学习能力强得多。训练多层网络需要更强大的算法,其中逆误差传播(Backpropagation,BP)算法是较为成功的神经网络学习算法。
下图为一个拥有d个输入神经元,l个输出神经元和q个隐含神经元的多层前馈神经网络。
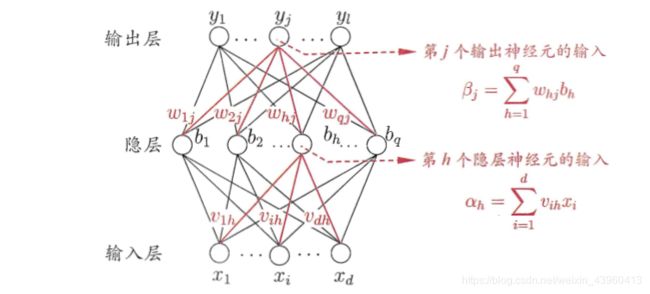
对于给定数据集
D={(x1,y1),(x2,y2),…,(xm,ym)},其中xi∈Rd,yi∈Rl
 假设隐含层和输出层的神经元都为Sigmoid函数,对训练例(xk,yk),假定神经网络的输出为
假设隐含层和输出层的神经元都为Sigmoid函数,对训练例(xk,yk),假定神经网络的输出为
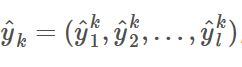 (3.1)
(3.1)
即:
![]() (3.2)
(3.2)
则网络在(xk,yk)上的均方误差为:
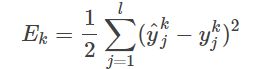 (3.3)
(3.3)
图上的网络中有(d+l+1)q+l个参数需要确定:
输入层到隐含层的dq个权值,隐含层到输出层ql,q给隐含层神经元的阈值,l给输出层神经元的阈值。
BP是一个迭代学习算法,在迭代的每一轮中采用广义的感知机学习规则对参数进行更新估计,任意参数v的更新估计式为:
![]() (3.4)
(3.4)
下面以隐含层到输出层的连接权whj来进行推导:
BP算法基于梯度下降的策略,以目标的负梯度方向对参数进行调整,对于误差Ek
和给定学习率η,有:
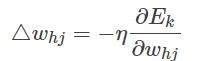 (3.5)
(3.5)
whj是先影响输出层第j个神经元,然后再进一步影响输出y^kj的。所以有:
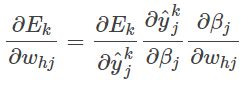 (3.6)
(3.6)
其中:
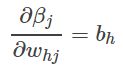 (3.7)
(3.7)
Sigmoid函数具有很好的性质:f′(x)=f(x)(1−f(x)) (3.8)
根据(3.3)和(3.4),有:
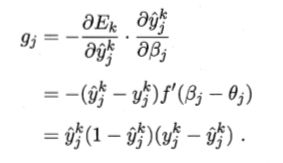 (3.9)
(3.9)
将(3.9)和(3.7)代入(3.6),就得到了BP算法中关于whj的更新公式:
![]() (3.10)
(3.10)
类似可得:
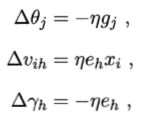 (3.11)
(3.11)
在后两个式子中
其中eh表示的是隐含层的梯度。其实根据前面的结构图,我们能够得到公式:
![]() (3.12)
(3.12)
所以有:
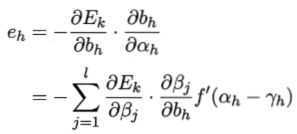
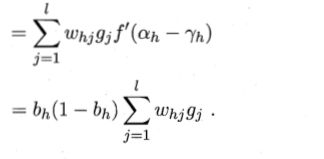 (3.13)
(3.13)
总结:

需注意的是,BP算法的目标是最小化训练集上的累计误差
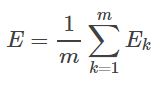
文档参考链接:
《机器学习》,周志华
《 统计学习方法》,李航
https://www.cnblogs.com/charlotte77/p/5629865.html
https://blog.csdn.net/u013555719/article/details/78783928