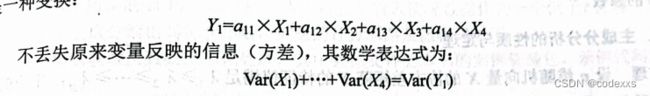数据挖掘学习笔记
第一章 python基础
1.4 python基本数据类型
#1.41数值类型
int,float,bool
#1.42字符串str
s1='abcd'
s2='''ab cd'''1.4.3列表List
L1=[1,'a1',2,'aa']
#[1, 'a1', 2, 'aa']1.4.4元组Tuple
处在元组中的元素不能修改
T1=(1,'a1')
T1=(1,'C1','A1')
#(1, 'C1', 'A1')
T1[1]=2
# 'tuple' object does not support item assignment
1.4.5集合
集合保持了元素的唯一性,对于重复的元素只取一个,集合不支持由序列取值
J1={266,3,'h'}
#{266, 3, 'h'}
J2={266,3,3,'h','a','A','h'}
#{'A', 3, 266, 'h', 'a'}
J2[0]
#'set' object does not support indexing1.4.6字典
①{键 : 值}
②键必须唯一,值不必唯一
③(1)键可以是数值,字符。
(2)值可以是数值,字符或者其他python数据结构
④需要由键取值
d1={1:1,'J':{266,2,2},'T':(3,'A'),'L':[5,5],3:'''6'''}
#{1: 1, 'J': {2, 266}, 'T': (3, 'A'), 'L': [5, 5], 3: '6'}
d1[3]
#'6'1.5 python公有方法
1.5.2切片
#通用
s2='hello world!'
s2[0:]
#'hello world!'
s2[0:1]
#'h'
#包左不包右
s2[:]
#'hello world!'
s2[-1]
#'!'
s2[0:5:2]
#'hlo'
#从s2[0]开始两步截取一次
#[开始索引:结束索引:步长]
s2[::-1]
#'!dlrow olleh'
1.5.3长度
(1)字符串的长度为字符串中所有字符的长度(空格也算)
(2)列表,元组,集合的长度为元素的个数
(3)字典的长度为键的个数
len(s2)1.5.4统计
字符串,列表,元组可以进行统计
s2='hello world!'
max(s2)
#'w'1.5.5确定成员变量
'e'in s2
#True1.5.6删除变量
s2='''ab cd'''
del s2
s2
# name 's2' is not defined1.6方法
1.6.1列表方法
L1=[1,'a1',2,'aa']
#1创建空列表
L=list()
#L=[]
#2添加元素
L.append('H')
#3扩展列表
L.extend(L1)#可以和元组做一下对比
#某元素计数
L.count('H')
#返回某元素下标
L.index('H')
#元素排序 需要同为str或者int时
L.sort()
1.6.2元组方法
#1创建空元组
T=tuple()
T=()
#2元素计数
T1.count('a1')
#3返回下标
T1.index('a1')
#4元组连接
T+T1 #和列表做一下对比1.6.3字符串方法
s1='abcd'
#创建空字符串
S=str()
#查找子串 查找子串开始出现的索引位置,没有找到则返回—1
#第一个参数为需要查找的子串,第二个参数为指定待查字符串的开始位置,第三个参数为指定待查字符串的长度
s1.find('a',1,len(s1))
#替换子串
#(被替换子串,替换子串)
s1.replace('a','aa')
#字符串连接 和元组一样用+ 和列表不一样
s1+S
#字符串比较
S==s11.6.4字典方法
#创建字典
d=dict()
d={}
#可以将嵌套元素转为字典(必须嵌套,length只能为2(1键1值))
d1=dict([[1,'aa']])
#获取字典值 由键获取对应的值
d1.get(1)
#字典赋值
d.setdefault(2,['a','b'])
# 第一种 若键不存在则会抛出KeyError异常
person['city']
# 第二种 不会抛出异常,不存在则返回None,也可以设置默认返回值
person.get('city',"上海")
# 第三种 与第二种类似,区别在于setdefault方法会更新字典
person.setdefault('city', '上海')
————————————————
版权声明:本文为CSDN博主「从小就拽」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/q5841818/article/details/805514131.9函数
1 无返回值
2有一个返回值
3有多个返回值
def work(r):
import math
c=2*math.pi*r
s=math.pi*r*r
return(c,s)
work(1)第二章 科学计算包numpy
1Numpy的核心基础是N维数组
数组中的元素要求同质即数据类型相同
(以下代码默认导入numpy包)
2.2.1创建数组
#嵌套列表(元素为元祖) 转为二维数组
L3=[(1,2),(3,4)]
L4=np.array(L3)
#嵌套元祖(元素为元祖) 转为三维数组
L5=((1,2),(3,4),(5,6))
L6=np.array(L5)#numpy多维数组中的子数组必须具有相同的长度
d3 = [[1,2,3],[4,5,6],[7,8,9,10]]
A33 = np.array(d3)2.2.2内置函数创建数组
#创建3行4列元素全为1的数组
z1 = np.ones((3,4))
#创建3行4列元素全为0的数组
z2 = np.zeros((3,4))
#创建默认初始值为0 默认步长为1 末值为9的一维数组
z3 = np.arange(10)
#创建初始值为2 步长为2 末值为9的一维数组
z4 = np.arrange(2,10,2)
#array([2, 4, 6, 8])
2.3数组尺寸
通过数组的shape属性返回数组的尺寸,返回值为元组
#一维数组 仅返回一个元素 代表这个数组的长度
d11 = np.array([1,2,3,4,5,7])
s11 = d11.shape
s11
#(6,)
#二维数组 返回元组中有两个值 (行数,列数)
d2 = [[1,2,3],[4,5,6],[7,8,9]]
A22 = np.array(d2)
s22 = d22.shape
s22
#(3, 3)
数组重排
r = np.array(range(10))
r1 = r.reshape((2,5))
r12.4数组运算
A = np.array([[1,2],[3,4]])
B = np.array([[5,6],[7,8]])
#A数组所有元素取平方 然后与B数组对应元素之间相除
C1 = A**2/B
#数学运算
M1 = np.sqrt(A) #取平方根
M2 = np.abs([-1,-2,10]) #取绝对值2.5数组切片
2.5.1常见的数组切片
#D[①,②] ①控制行下标 ②控制列下标 下标从零开始
#取所有行或所有列 用:代替
D = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
D12 = D[1,0] #访问行为1 列为0的数据
#5
D03 = D[:,[0,3]] #访问0,3列数据#*行控制 还可以通过逻辑列表来实现
D0 = D[D[:,0]>4,:] #取满足0列大于4所有列数据
D31 = D[D[:,0]>5,[3,1]] #取满足第0列大于4的3列数据 和 第0列大于5的1列数据
D31
#array([ 8, 10])TF = [False,True,True]
Dtf = D[TF,[3,1]]
Dtf
#array([ 8, 10])2.5.2 利用ix_()函数进行数组切片
数组切片也可以通过ix_()函数构造 行,列 下标索引器
D = np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12]])
print(D[:,0]>4)
#[False True True]
print(np.ix_(D[:,0]>4 ))
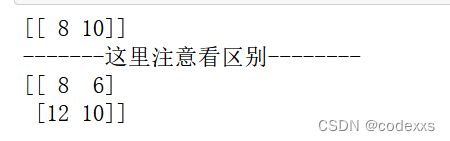
#(array([1, 2], dtype=int64),)Dix1 = D[np.ix_(D[:,0]>4),[3,1]]
print(Dix1)
print("-------这里注意看区别--------")
Dix2 = D[np.ix_(D[:,0]>4,[3,1])]
print(Dix2)2.6 数组连接
数组连接有水平连接【hstack()】和垂直连接【vstack()】两种方式
import numpy as np
A = np.array([[1,2],[3,4]])
B = np.array([[5,6],[7,8]])
C_s = np.hstack((A,B)) #水平连接要求行数相同
C_v = np.vstack((A,B)) #垂直链接要求列数相同
C_v2.7 数据存取
利用numpy包中的save()函数 ,可以将数据集保存为二进制数据文件,数据名扩展为.npy
#存
np.save('data77',C_v)#加载数据集
np.load('data77.npy')2.8数组形态变换
Numpy包提供了reshape()函数,ravel()函数用于改变数组的形状 不改变原始数据的值
#一维变二维
arr = np.arange(12).reshape(3,4)
#二维变一维
arr1 = arr.ravel()
2.9数组的排序与搜索
sort函数 直接将数组元素值按照从小到大的顺序进行直接排序
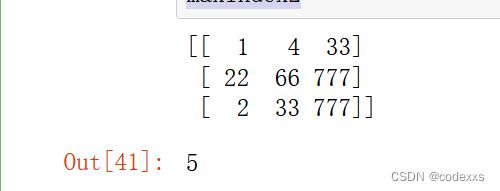
arr2 = np.array([1,4,33,22,66,777,2,33,777])
arr3 = np.sort(arr2)
#array([ 1, 2, 4, 22, 33, 33, 66, 777,777])argmax()和argmin()函数可以返回待搜索数组最大值和最小值元素的索引值
如果存在多个最大(小)值则返回第一次出现的索引值
maxIndex = np.argmax(arr2)
minIndex = np.argmin(arr2)
maxIndex
#5arr4 = arr2.reshape(3,3)
print(arr4)
maxIndex2 = np.argmax(arr4)
maxIndex2对于二维数组 可以通过设置axis= 0 或者 axis = 1来返回各列或者各行最大(小)值的索引值
maxIndex3 = np.argmax(arr4,axis = 0) #各列最大值的索引值
#array([1, 1, 1], dtype=int64)
minIndex3 = np.argmin(arr4,axis = 1) #各行最小值的索引值
#array([0, 0, 0], dtype=int64)2.10矩阵与线性代数运算
第三章 数据处理包Pandas
(本章默认导入numpy包和pandas包)
Pandas基于Nump而构建,可以处理不同数据类型
同时有十分利于数据处理的数据结构:序列(对象)(Series)和数据框(对象)(DataFrame)
3.2 序列
序列存储一维数据,有两部分组成,一部分是索引,另一部分是对应的值
①默认情况下索引从0开始按照从小到大的顺序排列,每个索引对应一个值。
s1 = pd.Series([1,-2,2,3,'hq'])
s1②可以通过指定列表,元组,数组创建默认序列
s2 = pd.Series(np.array([1,2,77]))
s2③可以通过指定索引创建个性化序列,也可以通过字典来创建序列,字典的键转化为索引,值为序列的值
s4 = pd.Series([1,-2,2,3,'hq'],index=['a','b','c','d','e'])
s4s3 = pd.Series({'red':200,'blue':1000,'yellow':222})
s3序列中元素的访问通过索引即可访问对应的元素值
s1[0]
#1
s4['a']
#1
s3['red']
#2003.2.2 序列属性
序列有两个属性(內部值),值(values属性)和索引(index属性),
s1 = pd.Series([1,-2,2,3,'hq'])
s1.values
#array([1, -2, 2, 3, 'hq'], dtype=object)
s1.index
#RangeIndex(start=0, stop=5, step=1)
#这里注意stop=5
s3 = pd.Series({'red':200,'blue':1000,'yellow':222})
s3.values
#array([ 200, 1000, 222], dtype=int64) #也是数组
s3.index
#Index(['red', 'blue', 'yellow'], dtype='object')3.2.3 序列方法
1 unique() 可以去掉序列中重复的元素值,使元素值唯一
S5 = pd.Series([1,'xl','xl',2,3,'pd'])
S5S51 = S5.unique()
S51
#array([1, 'xl', 2, 3, 'pd'], dtype=object)2 isin()方法 依次判断元素值的存在性。存在返回True
S5 = pd.Series([1,'xl','xl',2,3,'pd'])
S52 = S5.isin([1,'xl'])
S523 value4_counts()方法 统计序列元素值出现的次数
(有时也起到与unique()相同的效果,即去掉序列数据中的重复值,保障了 数据的唯一性,而且获得了重复的次数,在金融数据处理中被广泛应用)
S5 = pd.Series([1,'xl','xl',2,3,'pd'])
S53 = S5.value_counts()
S534空值处理方法
在序列中处理空值的方法有3个:isnull(), notnull() , dropna()
isnull()判断序列中是否有空值 是空值返回True 不是空值返回Flase
s6 = pd.Series([10,'hq','hq',np.nan])#np.nan为空值
s6.isnull()s6[s6.isnull()]
#3 NaN
notnull()判断序列是否有非空值 是非空值返回True 不是非空值返回flase
dropna()清洗序列中的空值可以配合使用空值处理函数
#~为取反 采用逻辑数组通过索引获取数据
s61 = s6[~s6.isnull()]
s62 = s6[s6.notnull()]
s63 = s6.dropna
#三者执行结果一样3.2.4序列切片
序列元素的访问是通过索引完成的,可以给定一组索引(列表或逻辑数组)来实现切片的访问
s1 = pd.Series([1,-2,7,'hq','dd'],index=['a','b','c','d','e'])
#索引连续
print(s1[0:2])
#索引不连续
s1[[0,1,3]]#索引为连续数组
s2 = pd.Series([1,2,4.5,7,9])
s2[s2>4]3.2.5 序列聚合运算
主要包括对序列中的元素求和,平均值,最大值,最小值,方差,标准差
s = pd.Series([1,2,4,5,6,7,8,9,10])
ssum = s.sum()
print(ssum)#52
smax = s.max()
print(smax)#10
smin = s.min()
print(smin)#1
#求平均值
smean = s.mean()
print(smean)#5.777777777777778
#求标准差
sstd = s.std()
print(sstd)#3.07318148576429543.3数据框
3.3.1数据框创建
坠了 写半天突然闪退了 竟然还没有没有保存 人在图书馆心在天堂
3.3.2数据框属性
3.3.3数据框方法
1dropna()方法
2 fillna()方法
3 sort_values()方法 指定列按值排列 对应列随之改变
dic2 = {'a':[7,2,9,6],'b':['a','q','4','r'],'c':[3,4,5,9]}
df2 = pd.DataFrame(dic2)
print(df2)
dfsv = df2.sort_values('a',ascending='False')#默认True为降序
dfsv4 sort_index()按照索引排序
5 head()方法读取数据集中前n行
6 drop()删掉数据集中的 指定列
7 join()两个数据框之间的水平连接
8 as_martrix() 将数据框转换为Numpy数组的形式
9 to_excel() 可以将数据框导出到Excel文件中
10 统计方法
(1)sum()方法求和
(2) mean()方法
3.2.4数据框切片
1 iloc属性
1 数据框中的iloc属性可以实现 下标值或者逻辑值定位索引并进行切片操作
2 访问或者切片的数据为DF.iloc[①,②]
(1)①为对数据框的行下标控制 ②为对数据框的列下标控制
(2)行列获取也可以通过:获取
(3)行控制还可以通过逻辑列表来实现
2 loc属性
1 数据框中的loc属性主要基于列标签进行筛选定位,再通过指定列从而实现数据切片操作
第四章 Matplotlib
这章主要介绍数据可视化包Matplotlib
1数据可视化时通过各种类型的图像来展现数据的分析结果或者分析过程
2可通过Matplotlib包中的pyplot模块实现常见图像的绘制
【以下默认导入】
import Matplotlib.pyplot as plt
import numpy as np
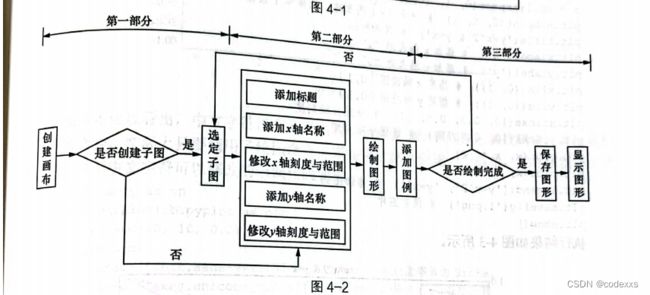
4.1.2 Matplotlib绘图基本流程
#第一部分 创建画布与子图
#1创建画布
plt.figure(1)
#2将figue分成不同块 实现分面绘图
plt.subplot(2,1,1)#分为2×1图形阵 选择第一张图片绘图
#第二部分 添加画布内容
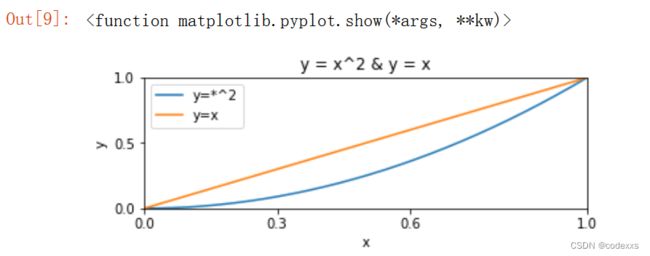
plt.title("y = x^2 & y = x") #添加标题
plt.xlabel("x") #添加x轴名称
plt.ylabel("y") #添加y轴名称
plt.xlim((0,1)) #指定x轴范围
plt.ylim((0,1)) #指定y轴范围
plt.xticks([0,0.3,0.6,1]) #设置x轴刻度
plt.yticks([0,0.5,1]) #设置y轴刻度
x = np.linspace(0,1,1000) #返回间隔类均匀的数值序列(start,stop,num)
plt.plot(x,x**2)
plt.plot(x,x)
plt.legend(['y=*^2','y=x']) #绘制图形之后添加图列
#第三部分 图形保存与展示
plt.savefig('1.png')
plt.show
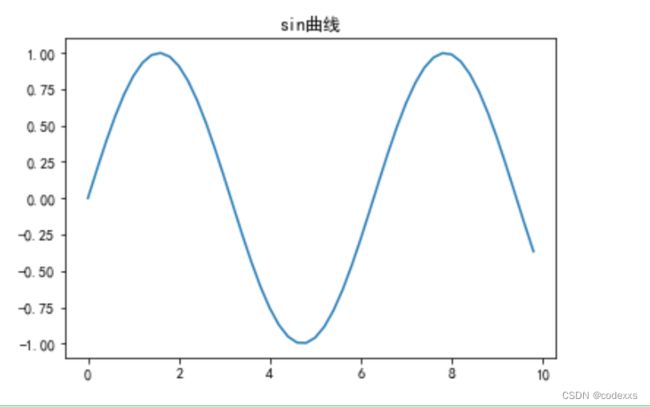
4.1.3中文字符显示
# 这里没有创建画布是因为 只要调用绘图命令 系统会默认创建画布
plt.rcParams['font.sans-serif'] = 'SimHei'#设置字体 否则中文无法正常显示
plt.rcParams['axes.unicode_minus'] = False
plt.title('sin曲线')
x = np.arange(0,10,0.2)
y = np.sin(x)
plt.plot(x,y)
plt.savefig('3.png')
plt.show()
4.2 Matplotlib常用图形绘制
1散点图的绘图函数scatter(x,y,[可选项]) 可选项包括颜色,透明度
4.2.1散点图
对D02日每日上车人数绘制散点图
数据是这样的(不知道咋上传文件)
#绘制某车次某日上车人数
#读取文件
data = pd.read_excel('car1.xlsx')
#筛选车次这列值为DO2的,指定日期,上车人数这两列,以日期值做降序排列
filterData = data.loc[data['车次'] == 'D02',['日期','上车人数']].sort_values('日期')
#设置x , y 值并绘图
x1 = np.arange(1,len(filterData.iloc[:,0])+1)
y1 = filterData.iloc[:,1]
plt.scatter(x1,y1)
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.title('D02车次上车人数散点图')
plt.xlabel('日期')
plt.ylabel('上车人数')
#设置x轴的数目和取值
plt.xticks([1,5,10,15,20,24],filterData['日期'].values[[0,4,9,14,19,23]],rotation = 90)
plt.show()4.2.2线性图
线性图的绘图函数为plot(x,y,[可选项])
数据依旧是‘车次上车人数统计’ ,绘制D02,D03车次上车人数线性图
data = pd.read_excel('car1.xlsx')
xd02 = data.loc[data['车次'] == 'D02',['日期','上车人数']]
x2 = np.arange(1,len(xd02.iloc[:,0])+1)
y2 = xd.iloc[:,1]
xd03 = data.loc[data['车次'] == 'D03',['日期','上车人数']]
x3 = np.arange(1,len(xd03.iloc[:,0])+1)
y3 = xd03.iloc[:,1]
plt.plot(x2,y2,'r*--')
plt.plot(x3,y3,'b*--')
plt.xticks([1,5,10,15,20,24],filterData['日期'].values[[0,4,9,14,19,23]])
plt.rcParams['font.sans-serif'] == 'SimHei'
plt.title('D02,D03上车人数走势图')
plt.xlabel('日期')
plt.ylabel('人数')
plt.legend(['D02','D03'])
plt.show()4.2.3 柱状图
柱状图的绘图函数为bar(x,y[可选项])
4.2.3直方图
直方图的绘制函数为hist(x,[可选项]),直方图的y轴往往表示对应的x的频数
4.2.4饼图
1饼图发绘图函数为pie(x,y,[可选项])
2 x表示待绘制的数据序列,y表示对应的标签,可选项表示绘图设置,这里绘图设置为百分比的小数位
4.2.6箱线图
4.2.7 子图
指在同一个绘图界面上绘制不同类型的图像
第五章 机器学习与实现
5.1 scikit-learn简介
scikit-learn的基本功能主要分为6大部分: 数据预处理,数据降维,回归,分类,聚类和模型选择
五种回归模型: 线性回归 多项式拟合 岭回归 Lasso回归 弹性网络回归(ElasticNet Regression)
五种分类模型:逻辑回归、神经网络,朴素贝叶斯、决策树、支持向量机、随机森林、
5.2 数据预处理
5.2.1缺失值处理
1 常用的三种填充方法为:均值填充,中位数填充,最繁值填充
填充方式有两种:按行,按列
2 按行均值填充或按列均值填充就是对某行或某列中所用缺失值用该行或该列非缺失值的平均值表 示
中位数填充和最繁值填充同理
3 填充的数据结构要求为数组或数据框,类型为数值类型
基本步骤如下:
import pandas as pd
import numpy as np
#数据填充前
c = np.array([[1,2,3,4,],[4,5,6,np.nan],[5,6,7,8],[9,4,np.nan,0]])
C= pd.DataFrame(c)
C#1导入数据预处理需要的填充模块Imputer
from sklearn.preprocessing import Imputer#2利用Imputer创建填充对象imp
imp = Imputer(missing_values = 'NaN',strategy = 'mean',axis=0)
#3调用imp中的fit()拟合方法,对待填充数据进行拟合训练
imp.fit(C)
#4调用imp中的transform方法,返回填充后的数据集
tc = imp.transform(C)
tc5.2.2 数据规范化
1防止由于变量单位不同导致模型失真需要对数据进行规范化处理
2两种常用的规范化处理方法:均值-方差规范化,极差规范化
①均值—方差规范化
数据是这样的
b = np.array([[1,999999,3,4,],[4,5,6,np.nan],[5,66666666,7,8],[9,4,np.nan,0]])
B= pd.DataFrame(b)
B#1进行规范化之前需要填充处理
imp1 = Imputer(missing_values= np.nan,strategy='median',axis=1)
imp1.fit(B)
tB = imp1.transform(B)X = tB
#2导入均值-方差规范化处理模块
from sklearn.preprocessing import StandardScaler
#3利用StandardScalar创建均值—方差规范化对象scaler
scalar = StandardScaler()
#4调用scalar对象中的fit拟合方法 对数据就行拟合训练
scalar.fit(X)
#5transform返回规范后的数据集
tX = scalar.transform(X)
tX②极差规范化处理
X1 = tB
from sklearn.preprocessing import MinMaxScaler
min_max_Scalar = MinMaxScaler()
min_max_Scalar.fit(X1)
min_max_Scalar.transform(X1)5.2.3 主成分分析
1在分析与挖掘中,遇到的众多变量之间往往具有一定的相关性
2如果众多指标之间具有较强的相关性,不仅会会增加计算复杂度,也会影响模型分析结果
3所以可以把众多的 变量转换为少数几个互补相关的综合变量,同时又不影响原来变量所反映的信息,这种方法在数学上成为主成分分析
如何定义和计算综合指标呢
5.2.4 主成分分析应用举例
#首先要进行数据预处理
X = data.iloc[:,1:]
#1空值填充
#①导入数据预处理需要的填充模块Imputer
from sklearn.preprocessing import Imputer
#②利用Imputer创建填充对象imp
imp = Imputer(missing_values = 'NaN',strategy = 'median',axis=0)
#③调用imp中的fit()拟合方法,对待填充数据进行拟合训练
imp.fit(X)
#④调用imp中的transform方法,返回填充后的数据集
tc = imp.transform(X)
tc
#2进行数据规范化
X1 = tc
from sklearn.preprocessing import MinMaxScaler
min_max_Scalar = MinMaxScaler()
min_max_Scalar.fit(X1)
X1=min_max_Scalar.transform(X1)
X1#对标准化后的X1做主成分分析
#①导入主成分分析模块PCA
from sklearn.decomposition import PCA
#②利用PCA创建主成分分析对象pca 设置累计贡献率在95%以上
pca = PCA(n_components=0.95)
#③调用pca中的fit()拟合方法,对待填充数据进行拟合训练
pca.fit(X1)
#④调用pca中的transform方法,返回提取的主成分
Y= pca.transform(X1)
Y#⑤返回pca对象属性
# 特征向量
tzxl = pca.components_
#特征值
tzz = pca.explained_variance_
#返回主成分方差百分比(贡献率)
gxl = pca.explained_variance_ratio_
#主成分表达式及验证
Y00 = sum(X1[0,:]*tzxl[0,:])
Y01 = sum(X1[1,:]*tzxl[0,:])
Y02 = sum(X1[2,:]*tzxl[0,:])
Y03 = sum(X1[3,:]*tzxl[0,:])#综合得分 = 各个主成分X贡献率之和
F=gxl[0]*Y[:,0]+gxl[1]*Y[:,1]+gxl[2]*Y[:,2]
dq=list(data['地区'].values) #提取地区
Rs=pd.Series(F,index=dq) #以地区作为index,综合得分为值,构建序列
Rs=Rs.sort_values(ascending=False) #按综合得分降序进行排序
pd.DataFrame(Rs,columns=['综合得分'])
课本P89稍后补上具体过程
5.3线性回归
5.3.1一元线性回归
#综合得分 = 各个主成分X贡献率之和
F=gxl[0]*Y[:,0]+gxl[1]*Y[:,1]+gxl[2]*Y[:,2]
dq=list(data['地区'].values) #提取地区
Rs=pd.Series(F,index=dq) #以地区作为index,综合得分为值,构建序列
Rs=Rs.sort_values(ascending=False) #按综合得分降序进行排序
pd.DataFrame(Rs,columns=['综合得分'])5.3.2多元线性回归模型
5.3.3 Python线性回归应用举例
数据是这样的
题目:
import pandas as pd
data = pd.read_excel('发电场数据.xlsx')
#1线性回归分析
#①确定自变量x和因变量y
x = data.iloc[:,0:4] #x = data.iloc[:,0:4].as_matrix
y = data.iloc[:,4]
#②导入线性回归模块
from sklearn.linear_model import LinearRegression as LR
#③创建线性回归对象lr
lr = LR()
#④调用lr对象中的fit()方法 对数据进行拟合训练
lr.fit(x,y)
#⑤调用lr对象中的score()方法,返回其拟合优度(判定系数),观察其线性关系是否显著
Rlr = lr.score(x,y)#判定系数R^2
#⑥取lr对象中的coef_,intercept_属性,返回x对应的回归系数和回归系数常数项
c_x = lr.coef_ #lr对象中的coef_属性
c_b = lr.intercept_ #lr对象中的intercept_
#2利用线性回归模型进行预测
#⑦预测
#方法①:利用lr对象中的predict()方法进行预测
import numpy as np
rx = np.array([11,22,33.3,55.5]).reshape(1,4)
#方法②:利用线性回归方程进行预测
r1 = x1*c_x
R2 = r1.sum()+c_b