KNN算法总结
概述
K最近邻(k-Nearest Neighbor,KNN)分类算法是最简单的机器学习算法。
KNN算法的指导思想是“近朱者赤,近墨者黑”,由你的邻居来推断出你的类别。
本质上,KNN算法就是用距离来衡量样本之间的相似度
机器学习,算法本身不是最难的,最难的是:
1、数学建模:把业务中的特性抽象成向量的过程;
2、选取适合模型的数据样本。
算法图示
从训练集中找到和新数据最接近的k条记录,然后根据多数类来决定新数据类别。
算法涉及3个主要因素:
1)训练数据集
2)距离或相似度的计算衡量
3)k的大小
算法描述
1)已知两类“先验”数据,分别是蓝方块和红三角,他们分布在一个二维空间中
2)有一个未知类别的数据(绿点),需要判断它是属于“蓝方块”还是“红三角”类
3)考察离绿点最近的3个(或k个)数据点的类别,占多数的类别即为绿点判定类别
算法要点
1,计算步骤
计算步骤如下:
1)算距离:给定测试对象,计算它与训练集中的每个对象的距离
2)找邻居:圈定距离最近的k个训练对象,作为测试对象的近邻
3)做分类:根据这k个近邻归属的主要类别,来对测试对象分类
2,相似度的衡量
距离越近应该意味着这两个点属于一个分类的可能性越大。
但,距离不能代表一切,有些数据的相似度衡量并不适合用距离
相似度衡量方法:包括欧式距离、夹角余弦等。
(简单应用中,一般使用欧氏距离,但对于文本分类来说,使用余弦(cosine)来计算相似度就比欧式(Euclidean)距离更合适)
3,类别的判定
简单投票法:少数服从多数,近邻中哪个类别的点最多就分为该类。
加权投票法:根据距离的远近,对近邻的投票进行加权,距离越近则权重越大(权重为距离平方的倒数)
算法不足之处
1,样本不平衡容易导致结果错误
如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。
改善方法:对此可以采用权值的方法(和该样本距离小的邻居权值大)来改进。
2,计算量较大
因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。
改善方法:事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。
该方法比较适用于样本容量比较大的类域的分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
采用Python语言实现一个简单案例:
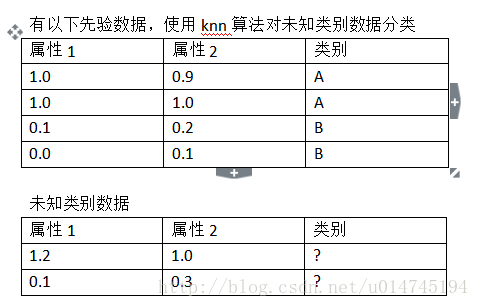
需求:
代码:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Author : xiaoke
from numpy import *
from operator import itemgetter
# 创建分类器
# inX:输入的待分类的向量
# dataSet:训练样本集
# labels:样本集中每个样本的标签
# k:选择最近邻居的数量
def classify0(inX, dataSet, labels, k):
# shape:数组每一维的大小
# dataSet.shape[0]样本数据有几行
dataSetSize = dataSet.shape[0]
# 样本数据有几列
# dataSetSize2 = dataSet.shape[1]
# 两个数组的差
# tile函数构造(dataSetSize,1)个copy
print(inX)
print(tile(inX, (dataSetSize, 1)))
diffMat = tile(inX, (dataSetSize, 1)) - dataSet
print(diffMat)
# 每行坐标计算平方
sqDiffMat = diffMat ** 2
print(sqDiffMat)
# 每行进行求和,axis=0,是每一列的和
sqDistances = sqDiffMat.sum(axis=1)
print(sqDistances)
# 开方即得到两个元素的欧氏距离,勾股定理
distances = sqDistances ** 0.5
print(distances)
# 对距离进行升序排序
sortedDistIndicies = argsort(distances)
print(sortedDistIndicies)
# 一个空的字典,用于存放
classCount = {}
for i in range(k): # 取前k个距离
# 得到升序排序后的距离所对应的的标签
voteIlabel = labels[sortedDistIndicies[i]]
print(voteIlabel)
# 对标签从零进行计数,对应的标签每出现一次加一
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
print(classCount)
# sorted函数对标签的个数进行降序排序
sortedClassCount = sorted(classCount.items(), key=itemgetter(1), reverse=True)
# 排序后第一个标签的个数最多,即认为待分类的向量归属于此标签
return sortedClassCount[0][0]
# 创建样本数据及其类别标签
def createDataSet():
# 样本训练集
group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1], [3.1, 3.4]])
# 每个样本所属的标签
labels = ['A', 'A', 'B', 'B', 'C']
return group, labels
if __name__ == '__main__':
# 简单分类器测试
group, labels = createDataSet()
res = classify0([0.2, 0.1], group, labels, 3)
print(res)
# 结果为:
# [0.2, 0.1]
# [[ 0.2 0.1]
# [ 0.2 0.1]
# [ 0.2 0.1]
# [ 0.2 0.1]
# [ 0.2 0.1]]
# [[-0.8 -1. ]
# [-0.8 -0.9]
# [ 0.2 0.1]
# [ 0.2 0. ]
# [-2.9 -3.3]]
# [[ 6.40000000e-01 1.00000000e+00]
# [ 6.40000000e-01 8.10000000e-01]
# [ 4.00000000e-02 1.00000000e-02]
# [ 4.00000000e-02 0.00000000e+00]
# [ 8.41000000e+00 1.08900000e+01]]
# [ 1.64 1.45 0.05 0.04 19.3 ]
# [ 1.28062485 1.20415946 0.2236068 0.2 4.39317653]
# [3 2 1 0 4]
# B
# {'B': 1}
# B
# {'B': 2}
# A
# {'B': 2, 'A': 1}
# B