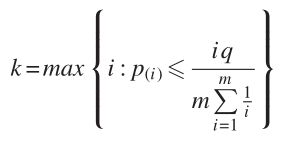投资学翻译2

提供美国平均月度股票回报独立信息的特征

在2011年美国金融协会主席演讲中，John H. Cochrane(2011, 1060)挑战研究人员找出提供美国股票平均回报独立信息的公司特征。Cochrane提出了他的挑战，因为在1970年以来的异常文献(Green, Hand, and Zhang 2013;侯、薛、张2016)。我们的研究目标是通过使用CRSP、Compustat和I/B/E/S中的94个特征开始响应Cochrane的号召;美国从1980年到2014年的回归提前一个月;以及避免增持微盘股的实证方法(Fama和French 2008;Hou, Xue, and Zhang 2016)，并对数据窥探偏差进行调整(Benjamini and Yekutieli 2001;Harvey, Liu, and Zhu 2016)。

我们的一般方法遵循Fama和French(1992)和其他人的方法，我们估计了一系列Fama- macbeth回归。然而，我们在四个方面背离了异常文献。首先，我们关注同时包括作为解释变量的所有94个大的企业特征，我们研究。这使我们能够识别那些提供独立、非冗余信息的特征。我们同时评估所有94个企业特征的方法是可行的，因为特征之间的平均绝对相关性很小(0.07)，而且我们通过将缺失特征值设置为当月非缺失值的标准化平均值来保留所有企业-月观察值。

其次，因为微型股——那些市值低于纽约证券交易所20个百分位数的股票——只占美国股市价值的3%，我们关注的是股票的横截面，以避免在微型股中过度权重(Hou, Xue, and Zhang 2015)。我们基于样本和方法的两种组合估计回归:对所有股票的市场价值加权最小二乘(VWLS)和对所有非微型股票的普通最小二乘(OLS)。前一种方法将最大的权重放在大盘股上，而后一种方法强调小股，但不是微股。我们将这两种方法的结果汇总在一起，以此来推断非微盘股票的大截面。为了证明微帽的影响并与之前的研究进行比较，我们还提供了使用OLS对所有股票的结果。

• 注意到由于使用大量回归器估计回归以及使用先前研究已经确定的特征而引起的数据窥探问题，我们通过使用Fama-MacBeth估计的坡度系数的双尾p值来评估一个特征是否具有统计学意义，该坡度系数调整了假检出率，考虑到假设检验的相关性，在我们的情况下，回归系数p值(Benjamini和Yekutieli 2001)。如果我们采用Harvey, Liu, and Zhu(2016)的建议，Fama-MacBeth t-statistic的绝对值大于等于3.0，那么我们的推论在很大程度上是相似的。
• 也是最后，我们根据技术、信息、交易量以及自1980年(我们的数据窗口开始之时)以来在美国资本市场发生的多/空投资工具的类型和能力方面的重大变化，评估了在日历时间内回报产生过程的稳定性。我们发现2003年基于特征的可预测性发生了显著变化，2003年后对冲投资组合对非微型股的回报降至零，独立特征的数量降至仅有两个。对于微盘，独立特征的数量也有所下降，而微盘对冲投资组合的回报在2003年后仍保持可靠的正。

我们通过建立一个常规基线来开始实证分析，以此来比较我们方法的结果。该基线包含了从1980年到2014年的全窗口回归的估计结果，其中包含94个特征中的每一个，作为一个独立变量，以及在Carhart(1997)、Fama和French(2015)以及Hou、Xue和Zhang(2015)等著名基准因子模型中，将因子的特征等量添加到一个给定的单一特征中作为解释变量。

我们发现只有一个94的特点是重要的(长期净营业资产的增长)当使用VWLS Fama-MacBeth回归包含单个特征对所有股票,这12个特征显著使用OLS all-but-microcap股票(资产增长,增长industry-adjusted销售,流通股百分比变化，库存增长，盈利公告回报，账面权益增长，资本支出增长，长期净运营资产增长，PP&E加库存增长，连续几个季度盈利高于去年同期，销售增长低于库存增长，以及标准化的意外季度收益)。通过这两种方法的汇集，在非微型股的横截面中总共产生了12个单因素显著特征，而在由微型股主导的横截面中则产生了30个单因素显著特征。这表明，在1980年至2014年的整整35年期间，作为异常现象提出的绝大多数特征并没有以单变量的方式稳健地呈现出来，特别是对于非微型股而言。

接下来，我们通过在控制了3或4个与显著基准因子模型相关的特征后单独评估特征来扩展单变量视角。在所有股票的Carhart、五因素和q因素模型上使用VWLS测试了90-91的6、4和1个显著特征，在所有微帽上使用OLS测试了17、4和4个显著特征。这表明，在显著因素激励的基准模型中，Hou、Xue和Zhang的q-theory模型最好地抓住了平均回报的独立决定因素，因为它产生的增量显著性企业特征比q-theory模型本身所规定的要少。

我们研究的中心是，我们放宽了每次评估一个非基准模型特征的方法，同时包括Fama-MacBeth回归中的所有94个特征。考虑到OLS的假设和特征之间较低的平均绝对交叉相关性，这使我们能够确定回报的独立决定因素。我们估计，在所有股票上使用VWLS估计有6个特征是独立的决定因素，而在全但微型股票上使用OLS估计有9个特征是独立的决定因素。通过这两种方法的汇集，在非微帽中产生了12个独立的特征:账面市值比、现金、分析师人数变化、收益公告回报、一个月动量、六个月动量变化、连续几个季度收益高于上年同期、年度研发对市值、回报波动、股票周转率、股票周转率、零交易日。相比之下，所有个股在以微帽为主的OLS横截面上有23个独立特征。

总的来说，我们对1980年至2014年全窗口期内美国股票平均月回报的决定因素的单变量和多变量研究结果表明了三个主要结论。首先,少量的多元的确定独立特征是一样的小数量的单变量显著特征(12)每次使我们认识到,它并非如此,一些独立的特征能够吸收大量的信息的其他特征单变量显著。相反，在调整了微股的影响和对数据窥探的担忧之后，本质上几乎没有什么特征能够独立预测非微股的平均回报。

其次，独立特征的同一性和性质不同于单一显著特征。基本和市场分类的基础上提出的异常麦克莱恩和教皇(2016),10的12单变量显著特征是fundamental-based(资产增长,增长industry-adjusted销售,库存增长,账面价值的增长,资本支出的增长,长期净营业资产的增长,PP&E的增长加上库存，盈利高于去年同期的连续季度数，销售增长低于库存增长，以及标准化的意外季度收益)，而两个是基于市场的(流通股的百分比变化，盈利公告回报)。相比之下，在12个多变量确定的独立特征中，只有一个是基于基本面的(连续几个季度的收益高于去年同期的数量)，而7个是基于市场的(6个月动量变化、收益公告回报、1个月动量、回报波动、股票周转率、股票成交量波动，零交易日)。这些差异表明，需要控制平均回报决定因素的研究可能最好使用我们确定的独立特征，而不是单一显著性特征。

• 作为非微盘回报独立决定因素的特征通常也是微盘回报的独立决定因素，但反之亦然。在非微帽的12个独立特征中，有10个是微帽的独立特征(所有个股均为OLS)， 23个微帽的独立特征中有13个是非微帽的独立特征。同样的情况是，非微盘的12个独立特征中有11个不属于卡哈特、五因素和q因素基准模型中的因素，但账面市值比除外。这表明，未来的工作可能会受益于开发平均回报模型，这些模型是量身定制的，以便考虑到不同公司规模的差异，而且它们所包含的特征比当前的基准模型更广泛。

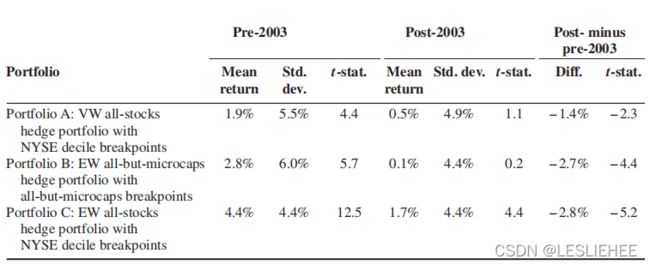
我们研究的最后一组结果扩展了前面的分析，表明独立特征的数量和经济重要性在历法时间上有显著的差异，并以不同的方式随企业规模而变化。具体来说，我们记录了在2003年，对冲投资组合回报的幅度急剧下降到基于特征的可预测性，特别是在非微型股中。在价值加权全股票对冲组合中，利用全部94个特征利用可预测性的平均月原始对冲收益从2003年前的1.9% (t-statistic = 4.4)下降到2003年后的0.5% (t-statistic = 1.1)。等权重全微盘股票对冲组合从2003年前的2.8% (t-statistic = 5.7)到2003年后的0.1% (t-statistic = 0.2)。对于微盘股而言，尽管2003年前后的平均月度原始对冲回报显著为正，但2003年之后的平均水平却要低近三分之二。将用于创建对冲回报的特征限制在前面提到的12个子集中，就可以得到类似的结论，控制Carhart、五因素和q因素基准因素模型的因素回报也是如此。

与对冲回报的显著下降相一致，我们还发现，2003年之后，只有两个特征是非微型股回报的独立决定因素，而2003年之前为12个。对于微型企业来说，独立决定因素的数量也有所下降，从25个下降到8个，下降了三分之二。因此,除了数据探测法和出版衰变,尽管低0.07平均互相关特性,自2003年以来的情况,几乎没有characteristics-based异常存在nonmicrocap截面的回报,只有不到十已经出现在微型截面。这表明，2003年特征的经济和统计意义向平均月度美国回报的转变，对过去和未来的研究都提出了有意义的挑战。

总的来说，我们的发现是，从1980年到2014年，94个特征中只有12个提供了独立的信息在非微帽中，2003年之后只有两个特征重要，这增加了对Harvey, Liu提出的先前研究结果的更多怀疑。朱(2016)对数据窥探的批评，以及麦克莱恩和教皇(2016)对出版后衰退的发现。虽然我们的结果与之前研究中记录的收益可预见性存在大量数据窥探问题的观点一致(Harvey, Liu, and Zhu 2016;Linnainmaa和Roberts 2016)，我们记录的可预见性与2003年前后以及公司规模的显著差异表明，数据窥探并不是一个完整的解释。

虽然我们无法确定2003年基于特征的可预见性突然下降的确切原因，但一种解释是，基于特征的可预见性反映了错误定价，而错误定价随着利用它的成本的下降而下降。与反映错误定价的基于特征的可预测性一致，Engelberg、McLean和Pontiff(2016)从一组97个特征中得出结论，异常回报是由于有偏见的投资者预期，因为它们在收益公告日高出7倍，在公司新闻日高出2倍，并可靠地预测分析师的预测误差。符合利用错误定价的成本下降随着时间的推移,我们注意到,许多变化发生在信息和交易环境从2002年7月到2003年6月,包括萨班斯-奥克斯利法案的通过,10的加速和10-Kfiling要求SEC,纽交所和设计师的介绍。虽然这些变化的时间合流使我们很难将其中一个或多个与我们在月度回报产生过程中观察到的变化联系起来，但我们建议，这些变化使快速实施定量多/空交易策略的成本更低，技术上也更容易。因此，与Shleifer and Vishny (1997)， Lesmond, Schill, and Zhou (2004)， Chordia, Roll, and Subrahmanyam (2008)， Li and Zhang (2010)， Lam and Wei(2011)的成本限制的论点一致，我们推测信息和交易环境的变化增加了套利活动，提高了股票市场的效率，并且在某种程度上，2003年之前显著的特征定价反映了套利的高成本限制，降低了特征在决定2003年后平均回报方面的影响。

1. 关于公司特征和股票回报截面的现有文献

我们的研究涉及三个主要研究领域。第一个是将平均回报模型作为一个函数，确定公司特征或受定价因素影响。这一领域的论文已经得出结论，基于少量特征的因子模型在很大程度上能够解释单个排序公司根据大量特征形成的投资组合回报(Hou, Xue, and Zhang 2015;Fama和French 2015, 2016)。例如,出于q-theory侯,天雪,和张(2015)发现一个因素模型组成的过剩的市场回报,small-minus-big大小因素,high-minus-low投资因素,和一个high-minus-low股本回报率因素执行类似于一个模型大小、账面值对市值,和12个月的动量，但也抓住了许多模式，不能解释这三个因素。因此，Hou、Xue和Zhang提出他们的四因子模型是其他因子模型的有力替代，任何新的异常变量都可以与他们的q因子模型进行基准测试，以确定异常是否真的提供了增量信息。在一个相关的方法中，Fama和French(2015, 2016)开发了一个五因素模型，通过增加盈利能力和投资因素(Li, Livdan, and Zhang 2009;不失为2013)。Light、Maslov和Rytchkov(2016)采用了完全不同的方法，将预期收益作为潜在变量，并开发了一种程序，根据特定特征将13个因素提取为两个新因素，他们认为其中一个因素总结了所有异常的信息。

我们的工作还与检验收益可预见性的研究有关。之前的研究发现，在套利摩擦程度最高的股票中，回报的可预见性最强，并且随着套利摩擦的减少和套利活动的增加，收益率也会随着时间的推移而下降。Lesmond, Schill, and Zhou (2004)， Hou and Moskowitz (2005)， Chordia, Roll, and Subrahmanyam (2008)， Li and Zhang (2010)， Lam and Wei(2011)都认为公司特征主要预测交易成本高或存在套利摩擦的股票的收益。与这一观点一致的是，Schwert(2003)、Green、Hand和Soliman(2011)、Hendershott、Jones和Menkveld(2011)、Chordia、Subrahmanyam和Tong(2014)、McLean和Pontiff(2016)发现，随着套利活动的增加或异常情况的公开，基于特征的各种异常的回报会下降。最近，Novy-Marx和Velikov(2016)观察到，虽然低周转率策略的回报对交易成本的调整是稳健的，但许多高周转率策略却不是。

我们的研究所涉及的第三个领域是一些研究，这些研究试图通过主要使用公司特征来衡量回报的维度，或者间接地通过使用无维度或低维度控制方法来编目已经被发现的显著的特征，或者直接将中型特征集放入多维模型中。Subrahmanyam(2010)确定了50个显著特征，以说明目录方法;Green, Hand, and Zhang(2013)列举了330个异常文献特征;Harvey, Liu, and Zhu(2016)列举了315个此类特征和/或因素;Hou, Xue, and Zhang(2016)进一步将基于异常的企业特征集扩展到430+。相反，Jacobs和Levy(1988)分析了25个特征，发现其中10个是显著的，Haugen和Baker(1996)的研究报告称，他们研究的40个相关特征中有11个是显著的Fama和French(2008)和Lewellen(2015)从发表的研究中选择的集合中发现，7个特征中有7个显著，15个特征中有10个显著同生在我们的研究中,DeMiguel et al。(2016)使用一个方法,结合公司特点为投资者的投资组合优化过程建模组合权重的函数特点找,6组50特点的研究共同重要预测因子。Stambaugh和Yuan(2016)从异常的因素定价观点发现，在1967-2013年间，除了市场和规模之外，一个包含两个错误定价因素的四因素模型可以容纳大量的异常。

尽管有这样的研究，但Cochrane(2011)提出的挑战仍然存在:在异常文献中的430多个特征中，只有一小部分被研究，以确定哪些公司特征提供了关于平均回报的独立信息。我们的论文回应了Cochrane的挑战，同时评估了比之前工作更大的一组特征，在这个更大的集合中，不仅估计了独立决定因素的数量、身份和经济意义，但最新强调的是，从1980年到2014年的整个数据期间，结果的程度随着时间的推移而变化，特别是在2003年前后。

1. 数据集的构建和企业特征之间的相关性

2.1按日历时间对齐的数据集

作为主要的目标,我们的论文是经验确定平均回报率的独立因素回归提前1个月回报率大量特性的同时,我们面临的设计决策,多少特征包括;如何将跨公司、跨时间段和跨数据库的特征结合起来;以及如何处理丢失的数据。为了最大化其他人复制和/或扩展我们的工作的能力，我们寻求透明地详细说明我们在选择、调整和编码公司特征时所做的选择。在这样做的时候，我们认识到我们的一些选择使我们远离确切的研究设计，特征定义，和在最初确定公司特征的论文中使用的样本周期。

我们首先从Green, Hand, and Zhang(2013)中列出的330个特征中选择了102个，要求每个特征完全可以从CRSP, Compustat和/或I/B/E/S数据中计算出来。我们的数据涵盖了从1980年1月到2014年12月的35年期间。我们从1980年开始，因为大多数特征只有在那一年才会出现。表1列出了我们选择的102个特征。附录提供了每个特征的细节，包括如何计算的描述和作者(s)，期刊，出版年或基础学术研究的工作论文。这些特征包括高被引论文和疏被引论文、已发表论文和工作论文以及1977 - 2016年的出版日期。有时，一篇论文中会出现不止一个特征。

我们首先对所有在纽约证券交易所、美国证券交易所或纳斯达克拥有普通股的公司进行数据创建，这些公司在其年度财务报表中有CRSP的月底市值和普通股价值缺失。然后，我们在Compustat、I/B/E/S和crsp中整合数据，计算并对齐日历时间中的特征。由于Green、Hand和Zhang(2013)的报告显示，在他们列出的330个特征中，57%的特征都是由最初的作者通过月度回报的视角来评估的，我们每个月都会重新衡量和调整特征。对于每个月t的收益，我们计算特征时，它们是在第t−1月底，假设年度会计数据在第t−1月底可用，如果公司的财政年度在第t−1月底结束至少6个月，如果该财政季度在第t−1月底之前至少四个月结束，则季度会计数据可在第t−1月底获得。I/B/E/S和CRSP数据使用I/B/E/S统计周期日期和CRSP月或日结束日期在日历时间中对齐。

虽然月度更新与许多量化机构投资者使用的投资组合再平衡方法一致，但我们认识到，一些从业人员每分钟更新一次数据，或者每12个月更新一次。我们选择每月更新，因为我们认为它是较低的交易和较长频率的交易成本之间的合理权衡，以及更大的及时性的好处(Novy-Marx和Velikov 2016年)。我们的选择意味着，在我们的数据集中，来自于低于月频率的研究的那些特征将不如原始研究中的及时，而那些来自于使用较长频率的研究的那些将更及时。这种下滑可能会降低我们检测个体特征增量意义的能力，但它也降低了我们识别无法在高周转率策略的交易成本影响下生存的回报可预测性的机会(Novy-Marx and Velikov 2016)。

我们从CRSP获取每月的股票回报，包括Shumway和Warther(1999)的退市回报。我们删除了20个月回报小于−100%的观察值，并将analyst following、nanalyst的空白值设为零。I/B/E/S是我们数据库中对公司的覆盖范围和可用性最严格的，所以我们从1989年1月开始只使用基于I/B/E/的特征，那时I/B/E/S开始更广泛的覆盖范围。根据Hou、Xue和Zhang(2015)以及Fama和French(2015)等人之前的研究，我们根据他们每月在纽约证券交易所的百分比来划分公司规模分组。我们标签股票市值大于中位数纽交所股票在月末t−1一样大,股票低于中位数以上20百分位小,股票值小于或等于20百分位微型,除微小市值外其他股票和股票贬值三除外。

因为在我们的关键分析中，我们通过同时对所有特征的提前一个月的回报进行回归，来确定平均回报的独立决定因素，在这种回归中，我们避免仅仅因为某个特征的价值在一个或多个公司月里消失而放弃它。从1980年1月到2014年12月，只有4%的特征具有完整的数据，没有遗漏观测。为了尽可能多地保留特征信息，我们采取的方法是首先对其月分布的第1和99个百分位数的所有特征进行winsorize，并将每个特征标准化，使其具有零均值和单位标准差。然后我们将缺失的特征值设置为特征的后标准化月平均值0对于每个公司特征，我们在表2中报告了1980年1月至2014年12月期间1,933,898个公司月观测的数据集的数量，没有遗漏的数据，以及在重置为零之前遗漏的百分比。我们注意到，丢失数据最多的特征往往是那些使用I/B/E/S分析师信息的特征(chfeps, disp, fgr5yr, nanalyst, sfe，和sue)，或者使用稀疏填充的Compustat数据的特征(rd_mve, rd_sale，和realestate)。

2.2企业特征之间的相关性

在Fama-MacBeth回归中，我们通过测量102个企业特征的初始集合之间的相互关系来衡量多重共线性关注点的潜力。虽然多重共线性不会导致估计斜率系数的偏差，但会增加其标准误差。因此，在某种程度上，我们能够排除与其他特征有很大交叉相关性的特征，因为它们是机械或经济相关的，例如，Beta和Beta平方——当我们估计同时包含大量特征的回归时，特别是当发现高度共线特征的数量很小时，我们期望能够更有力地识别平均回报的独立决定因素。

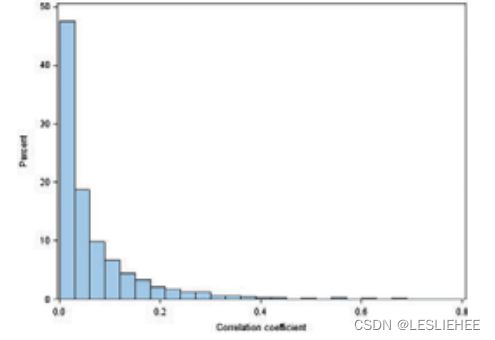
因此，我们计算每个特征的方差膨胀因子(vif)，因为vif概括了一个给定特征被所有其他特征的线性组合解释的程度(Greene 2011)。表3面板A描述了vif的分布。虽然VIF的中位数为1.8并不大，但VIF是正确偏斜的，因为10%的特征有VIF ?9.8。因此我们试图减轻多重共线性的影响,我们的重点回归,同时包括所有特征的八个特征最密切相关的其他特征(betasq、dolvol lgr, maxret, mom6m, pchquick,快,和stdacc),每一种都有一个VIF > 7。然后，我们在整个分析过程中使用剩下的94个特征。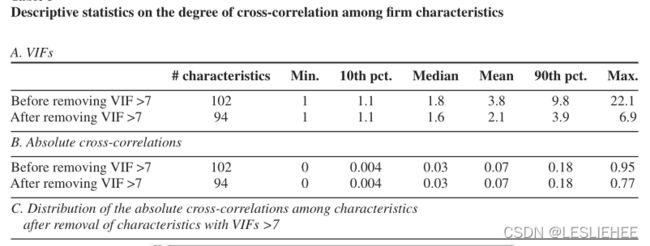

 

 

在表3的面板B中，我们报告了去除vif大于7的8个特征之前和之后的特征之间的绝对交叉相关性的关键百分位数。在这两种情况下，平均和中位数的绝对相互关系都相当低，分别为0.07和0.03毫不奇怪，在去除vif >7的特征后，最大的相互关系也下降了。面板C显示了94个非高度相关特征的绝对相互关系的分布，表明90%的绝对相互关系在0.2以下。

1. 经验方法与结果

我们估计标准法玛和麦克白(1973)回归在此期间从1980年到2014年,以确定有多少和我们组的94个公司特征显著因素提前1个月的回报,尤其是当他们都同时包含在回归。在评估有关平均回报率是否可靠的特点,我们的推论偏见,可能出现在我们的测试中从数据窥探或增持的微型股,占平均只有3%的市值NYSE-Amex-NASDAQ宇宙(法玛和法国2008;侯、薛、张2016)。

为了避免后一种偏见，我们将大部分分析集中在非微股截面公司上，采用两种方法:对所有股票应用价值加权最小二乘(VWLS)，对所有但微股使用OLS。VWLS方法将大部分权重放在大盘股上，而OLS方法则强调较小(但不包括微盘)的股票。这种方法类似于创建投资组合时，寻求最小化微盘股的影响(Hou, Xue, and Zhang 2016)。在得出关于非微帽的推论时，我们将两种方法的结果汇集在一起，而为了参考目的，我们对所有股票使用OLS得出倾向于微帽的推论。

在我们的设置中，考虑到我们的目标是评估单个特征的重要性，而不是所有特征作为一个单一集合的联合重要性，我们将面临纯粹偶然地错误地拒绝某些特征的零的风险。这种多重检验的担忧在其他研究文献中很常见，最近Harvey、Liu和Zhu(2016)在收益预测的背景下提出。而担心他们地址是新回归预测可能会错误地认为统计学意义,因为测试使用相同的数据集,我们担心的是,错误地认为回归预测风险具有重要意义,因为我们同时包含大量特性相同的回归,以及/或因为我们使用相同的数据集来估计多个回归。我们试图通过评估一个特征上估计系数的统计显著性来做到这一点，使用双尾p值对假检出率进行调整，并考虑到一组给定估计回归的p值之间的相关性(Benjamini和Yekutieli 2001)我们将这些p值称为DFDR p值，并要求DFDR p值小于或等于0.05，以认为相关参数估计有统计学意义。DFDR程序通过假设有一些测试统计数据的预期比例将被错误地判断为显著，从而控制错误发现率，之前的工作表明，这可能是我们研究的大量异常的情况。如Benjamini和Yekutieli(2001)所示，应用DFDR程序产生p值，导致错误发现率小于或等于期望的置信水平。

DFDR方法是通过对假设检验中的p值(在我们的例子中，是回归分析中系数的t统计量)进行排序来实现的，因此，对于m检验统计量，p值是有序的p(1) ≤p(2) ≤p(3) ≤…≤p (m)。为了达到期望的显著性水平q(0.05)，定义一组p值

 

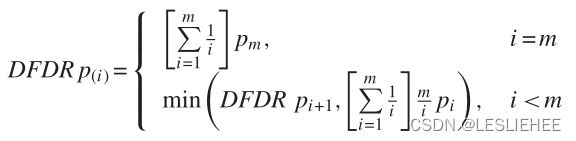
这个过程逐步遍历每个p值，从最显著的(最低的p值)开始，直到k达到使下一个p值不再满足标准。假设1到k被选为显著性，或者更准确地说，零假设被拒绝。DFDR p值由下式给出:

 

根据Harvey、Liu和Zhu(2016)的方法，我们还报告了绝对值大于或等于3.0的t统计量的数量，其中t统计量是从平均每月系数估计的时间序列中计算出来的，考虑到new - west(1994)超过12个月的调整滞后。

3.1平均收益的基线模型

我们首先建立一个常规基线，以此来比较我们同时包括Fama-MacBeth回归中的所有94个特征的主要方法的结果。这个基线包含估计回归的结果包含的94个特征作为一个独立变量,其次是回归,添加特征因素的等价物的基准因素模型Carhart(1997),法玛和法国(2015年),和侯,雪,Zhang(2015)使用1980-2014年的数据作为整体，这是基准模型中唯一没有的特征之一。

在表4的A列中，我们详细介绍了将每个特征单独放入Fama-MacBeth回归的结果，然后在B - D列中，将每个特征单独添加到给定基准模型所要求的特征的结果。Carhart模型的基准特征包括规模、账面市值比和12个月的动量;规模、帐面市场、投资、经营盈利为五要素模型;以及q因子模型的规模、投资和季度股本回报率。在每一列中，我们使用WLS报告所有股票的结果，使用OLS的所有微盘股票，以及使用OLS的所有股票。为了帮助读者了解哪些系数是显著的，考虑到研究的大量特征，我们用DFDR p-value ≤0.05对系数估计的t统计量进行加粗。具有DFDR p-值的系数估计值有多少≤0.05和t-statistics ≥3.0的绝对值见表4的第一行和第二行。

根据系数估计与DFDR假定值≤ 0.05,94年列一个我们发现只有一个特征是重要的在单变量回归non-microcapfirms以VWLS所有股票(长期净营业资产的增长),而12特征显著all-but-microcaps上使用OLS(资产增长,调整后的行业销售增长、流通股增长、库存增长、盈利公告回报、账面权益增长、资本支出增长、长期净运营资产增长、PP&E加库存增长，连续几个季度盈利高于去年同期。销售额的增长减少了库存的增长，以及标准化的意外季度收益)。对非微帽横断面的两种测量方法进行池化，共产生12个单变量显著特征，与对所有非微帽使用OLS所发现的特征相同。我们注意到，当微股被赋予与大股相同的回归权重(所有股票，OLS)时，有30个显著特征因此，Column A的结果表明，在之前的文献中提出的大多数特征作为异常，总的来说，在1980 - 2014年期间，并不是以单变量的方式稳健地存在。此外，在它们确实存在的地方，它们集中在微型股中。

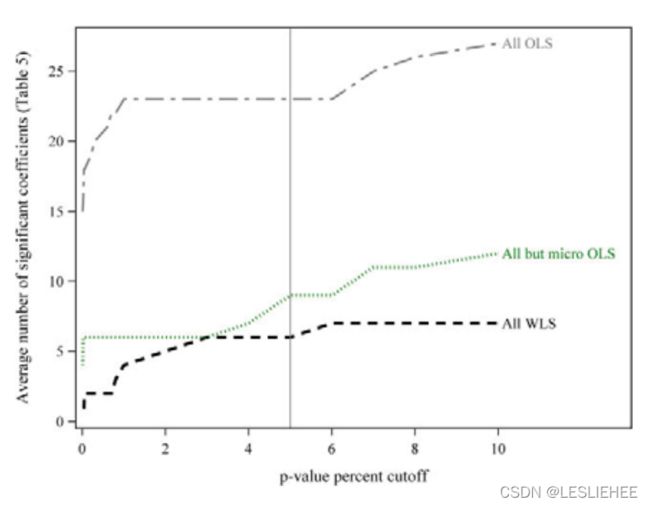
我们注意到，我们对显著系数的数量和身份的评估依赖于我们确定哪些系数可能是由样本内数据过拟合驱动的能力。我们推断大量系数是不显著的，这与之前的研究不同，因为我们不强调微帽，因为我们使用DFDR p值调整统计显著性，考虑了多次测试。在图1中，我们直观地展示了表4中使用DFDR p-值认为显著的系数的数量随DFDR p-值高于或低于我们的5%临界值而变化的方式。在非常低的统计显著性水平下(p值<.01)，有统计学意义的系数的数量变化最大。在我们的5% p值截止点附近，图1中的曲线相对平坦，这表明在表4的任何给定列中，显著系数估计的数量对p值截止点是1%、5%还是10%相对不敏感。更引人注目的是，我们的方法在强调微帽(所有股票都是OLS)或不强调微帽(所有股票都是VWLS，而所有非微帽都是OLS)的方法中，显著特征数量上的差异。总体而言，图1显示了多重测试的价值，以及在推断基于特征的平均月度回报可预测性的程度时，微帽的不成比例影响。

列的表4表明,当罪犯单独添加Carhart,大五,和品质因数模型,它是6,4和1使用VWLS增量显著特点在所有股票,和17,4,4 all-but-microcaps使用OLS增量显著特点。由于列B-D也表明，除了基准模型本身的显著特征外，q-因素模型导致的显著特征数量最少，我们推断，在三个有意的低维度基准模型之间，q-因素模型最好地捕捉了平均回报的横截面变化。我们的结论与Hou、Xue和Zhang(2015, 2016)的结论相呼应，他们进行了类似的测试，但使用了Carhart、五因素和q因素模型的因子版本。表4还强调了q因素和五因素模型相对于Carhart模型的表现的一个原因:这些模型包括一个增长的衡量指标，当考虑一次一个特征的回报可预测性时，这是很重要的。

3.2通过同时包括Fama-MacBeth回归中的所有94个特征，识别美国平均月收益截面的独立决定因素

表5显示了放宽表4中的单变量方法，同时包括Fama-MacBeth回归模型中所有94个特征，单独评价非基准模型特征的结果，使用从1980年到2014年的整个时期。考虑到OLS的假设，我们认为这种方法使我们能够最有力地确定平均回报的独立决定因素，我们期望，当所有其他特征的影响得到控制时，只有那些真正独立决定收益的特征才会有显著的估计系数。

基于DFDR假定值,列一个表5显示的时期从1980年到2014年,共有六个特征是可靠的独立因素当使用VWLS应用于所有股票(账面值对市值、现金月势头,六个月的动量变化,回报波动性和零交易日)的数量。这增加到9个特征如果应用OLS all-but-microcaps(现金,分析师的数量变化,收益报告回来,一个月势头,连续的季度收益增加一年前在同一季度,年度研发的市值,回报波动性,分享营业额,以及股票交易的波动性)。将这两种方法综合起来，可以产生12个多变量确定的独立特征，即账面市值比、现金、分析师数量变化、收益公告回报、一个月动量、六个月动量变化、连续几个季度收益高于去年同期的数量，年度研发到市值，回报波动率，股票周转率，股票周转率，零交易日。如表4所示，微盘股的不成比例影响可以从表5的C列中看出，应用OLS对所有股票产生23个独立特征。在图2中，我们直观地展示了表5中显著系数的数量作为DFDR p值与我们的5%截止值不同的函数，注意到如图1所示，曲线是相对平坦的，特别是对于非微帽。

 

综上所述，表4和表5的结果表明了1980年至2014年期间平均每月股票回报的独立决定因素的数量和性质。首先，在我们的94个特征样本中，有12个特征为非微型股提供了可靠的独立信息，而其余的82个则不是。这种对比描绘了先前研究中所作推论的不可靠的画面。

第二,多元的数量确定的事实独立特征的数量是一样的单变量显著特征(12)表明它并非如此,几个独立的特征能够有力地吸收大量的单变量中包含的信息的重要特征。相反，从本质上看，几乎没有什么特征能独立预测非微型股的平均回报。

• 独立特征的同一性和性质与单一显著特征的同一性和性质有本质区别。通过基本和市场分类方法提出的异常麦克莱恩和教皇(2016),我们分类10的12单变量显著特征为基础(资产增长,增长industry-adjusted销售,库存增长,账面价值的增长,资本支出的增长,长期净营业资产的增长,PP&E的增长加上库存，连续几个季度收益高于去年同期，销售增长低于库存增长，以及标准化的意外季度收益)，两个季度以市场为基础(流通股的百分比变化，以及收益公告回报)。相比之下，在12个多变量确定的独立特征中，只有一个是基本面特征(盈利高于去年同期的连续季度数量)，而7个是基于市场的(6个月动量变化、盈利公告回报、1个月动量、回报波动、股票周转率、股票成交量的波动性，以及零交易日)。这些差异表明，需要在设计中控制平均回报决定因素的研究，通过使用我们确定的独立特征，可能会发挥最强大的作用。
• 非微帽中的独立特征倾向于微帽中的独立特征，而非微帽中的独立特征。在非微盘的12个独立特征中，有10个在所有个股的OLS回归中是独立特征，23个微盘的独立特征中有13个是非微盘的独立特征。同样，12个独立特征中有11个不同于Carhart、五因素和q因素基准模型中的特征，账面市值比是一个显著的例外。这表明过去的研究使用了特征版的卡哈特五因素，和品质因数模型控制以外的平均回报率中代表性变量的特定的独立变量的重点工作可能没能达到预期的程度的控制,尤其是在某种程度上,公司正在研究的集合组成大型股股票。

在表6中，我们评估了从表5得出的结论的稳健性，即从1980年到2014年期间，非微型股的平均月收益有12个独立的决定因素。具体来说，表6报告了表5中报告的回归分析的估计结果，其中作为自变量的特征仅限于表5中被多变量确定为独立决定因素的12个。对列A和列B的检查表明，与表5中由DFDR p-value确定的6和9个独立决定因素相比，表6中可以看到类似的5和7的数字。同样地，表6中的列a和列B总共有9个特征，而表5中只有12个特征。我们注意到，在比较表5和表6时，与Carhart、五因素和q因素模型中的因素相等的特征的唯一代表，即账面市值比，在表6中并不显著。

3.3利用特征预测收益横截面来对冲投资组合收益

由于统计意义并不一定转化为经济重要性，在这一节中，我们报告了对冲投资组合测试的结果，该测试旨在测量在预测一个月前回报横截面时，利用全套特征所带来的经济效益的大小。具体来说，按照Lewellen(2015)的方法，在表7的panela中，我们报告了三个平均一个月持有期样本外对冲组合原始回报的幅度和显著性，计算结果如下。

在面板A中，对于从1990年1月开始的每个t−1月，我们使用从t−120月到t−1月的数据来估计与表5列A、B和C中报告的相同的三组回归。如表4 - 6中,我们假设年度会计数据可用t−1月结束时,如果该公司的财政年度结束前至少六个月月底t−1年度数据,季度会计数据可用在月末t−1如果多于公司季度结束前至少四个月月底t−1。对于每一列中定义的一组股票，我们分别在每家公司的基础上，将得到的平均系数估计值应用于t−1月底对应的94个特征的值。每个公司在第t个月有3个预期收益，A, B列各1个，然后，我们通过使用两种类型的断点来识别位于预测收益的顶部和底部十分位数的公司，以及在每个十分位数内加权单个实现收益的两种方法来计算第t个月三个对冲组合各自的实现收益。

对于表7面板A中的列A投资组合(标记为投资组合A)，十分位断点仅基于纽交所(所以每个十分位中有相同数量的纽交所股票，但不一定是整个纽交所、美国证券交易所、美国证券交易所、美国证券交易所、美国证券交易所、以及纳斯达克综合指数)和上/长、下/短十分位上的实际收益由公司在第t - 1月底的市值加权。对于列B组合，简称为组合B，十分位断点是基于几乎全是微盘股票的，在上/长、下/短十分位中实现的收益是同等加权的。最后，对于列C的投资组合(标记为投资组合C)，十分位断点基于纽约证券交易所股票，在上/长、下/短十分位中实现的回报是平等加权的。由于每个公司的预期收益在每个月的月底都是可用的，所以我们的方法在理论上是可以使用历史可用数据实时实现的。总的来说，应用该方法，从1990年1月到2014年12月，对于三个对冲组合a、B和C，每个组合产生了274个已实现的原始月度对冲回报的时间序列。

小组A报告对已实现的原始每月对冲投资组合回报的描述性统计。检验表明，所有三种类型的对冲投资组合的平均原始回报在统计上和经济上总是很大的，最大(最小)在最小(最大)的公司。对于由投资组合A的大众全股票多头顶/空/底十分位对冲组合(纽约证券交易所十分位断点)测量的股票截面，1990-2014年的平均原始月回报率为1.2% (t-statistic = 3.8)。而投资组合B的EW全但微股对冲组合使用全但微股十分位点来衡量股票的横截面，平均月原始回报为1.4% (t-statistic = 4.5)。这些结果表明，在所有94家企业特征的全部集合中使用可预测性有很大的经济效益。与此同时，我们注意到(再次强调了微型股可以发挥的不均衡影响)，投资组合C的EW全股对冲组合的平均月原始回报为3.1% (t-statistic = 11.3)。

面板B一样的统计报告面板,但使用预测收益构造顶部/长,底部/空十分位数基于限制的公司特征子集12表6所示,少一些分析师的变化因为分析师数据不可用在样本数据窗口。面板C的汇总报告的差异意味着对冲返回面板A和B可以看出限制对冲投资组合的构建旨在利用characteristics-based可预测性12特征识别表5列A和B的减少意味着对冲的回报材料和统计重要的方式，特别是对大型企业。投资组合A的平均对冲收益下降了三分之二，从1.2%下降到0.4% (t-statistic on difference = 3.0)，但投资组合B的平均对冲收益下降了三分之一，从1.4%下降到1.0% (t-statistic on difference = 2.2)。我们注意到通过表5,虽然确定了23个不同的独立特征在微型股(列C),限制对冲投资组合回到建设12个特征中标识列A和B表5只减少了意味着对冲回到微型组合的四分之一,从3.1%到2.4% (t-statistic on difference = 4.0)。当使用完整的公司特征来预测收益时，对冲投资组合的收益更高，这一发现似乎与回归结果相矛盾，回归结果表明只有一小组独立公司特征。然而，我们注意到，从投资组合的角度来看，用于确定单个回归系数显著性的统计调整可能过于保守。此外，由于对冲投资组合的回报是基于可能从对同一数据的多次测试中偶然发现的异常，在创建对冲投资组合回报时包含大量特征可能会加重多重测试的担忧。

3.4 2003年可预测性的变化，以及2003年前后美国股票平均月收益独立决定因素的数量和经济重要性的差异

表4-7描述的结果与异常和资产定价文献中的几乎所有研究一致，将1980-2014年作为一个统一的日历时间块，在此期间，假定收益生成过程保持不变。鉴于从1980年到2014年发生的股票交易量、性质和交易成本的重大变化，我们现在放松了这一假设，包括Reg。FD，交易报价的十进制化，萨班斯-奥克斯利法案，加速了SEC的备案要求，自动报价，以及计算机化的多头/空头定量投资(Chordia, Roll, and Subrahmanyam, 2001;琼斯2002年;Schwert 2003;法国2008年;Green, Hand, and Soliman 2011;Hendershott, Jones，和Menkveld 2011)。

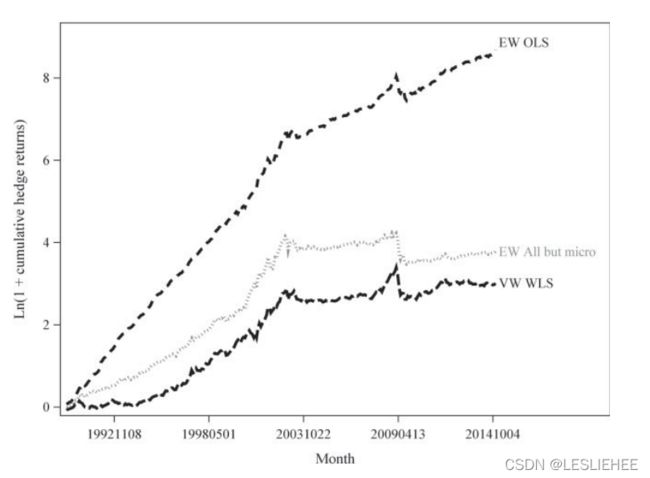
我们采用的第一种方法来评估在日历时间中收益产生过程的稳定性，如图3所示，在这里我们绘制1加上累计平均原始对冲投资组合收益的自然对数，其计算方式与表7的panela中的方式相同，但需要I/B/E/S数据的七个特征已被排除，因为I/B/E/S数据从1990年开始才切实可用。对图3的目视检查表明，在2002年末/ 2003年初，三个投资组合的平均对冲回报均呈现出急剧和持续的下降。事实上，非微型股的跌幅如此之大，以至于自2003年初以来，基于特征的对未来一个月美国回报的可预测性平均为零，只对微型股具有经济意义的可预测性，而且这种可预测性大大降低了。

我们在表8中提供了与这些可视化评估一致的统计证据，在表8中，我们报告了三个对冲组合在2003年之前、2003年之后和2003年之前的平均原始对冲回报，以及它们的相关t统计数据。我们把2003年以前定义为2002年12月31日结束的时期，2003年以后定义为2004年1月1日开始的时期。大众全股票对冲组合的平均原始月对冲回报(NYSE十分点)从2003年之前的1.9% (t-statistic = 4.4)下降到2003年之后的0.5% (t-statistic = 1.1)，其中−1.4%的月下降可靠地为负(t-statistic =−2.3)。类似地，具有所有微型股十分位数断裂点的EW全但微型股对冲组合的平均原始月对冲回报从2003年之前的2.8% (t-statistic = 5.7)下降到2003年之后的0.1% (t-statistic = 0.2)，其中−2.7%的2003年后与2003年前的降幅可靠地为负(t-statistic =−4.4)。相比之下，虽然EW全股票对冲投资组合的平均原始月收益在2003年之后比2003年之前下降了显著的2.8% (t-statistic =−5.2)，但在2003年之后仍然是可靠的正收益，平均每月1.7% (t-statistic = 4.4)。总之,经济对冲收益的可预测性程度在94年的集合特征研究暴跌在所有大小的公司,并且非微型股股市下跌如此之大,自2003年以来平均对冲回到利用基于特征的可预测性是无关紧要的不同于零。只有在微型股中，基于特征的可预见性存在，对这些公司来说，2003年后的经济可预见性比2003年前减少了三分之二。

 

表9通过报告与表5相同的Fama-MacBeth回归的估计结果，确认了从表8中平均对冲收益的推断，但分别针对1980-2002年和2004-2014年的子时期。我们首先关注列A和B在每个亚纪,这对我们的报告结果twoalternative non-microcapfirms的定义,在分析表5,我们测量的独立因素平均回报率的不同特点在A和B列组合,DFDR假定值吗?0.05。对列A和列B的检查表明，从1980年到2002年，12个特征是非微型股平均回报的独立决定因素，相比之下，2004年到2014年有两个特征。我们注意到，对于后者，一个是2003年之前和之后的独立决定因素(连续几个季度的收入高于上年同期的数量)，而另一个不是(行业调整后的雇员人数变化)。我们还从两个c列注意到，对所有股票使用OLS的独立决定因素的数量从2003年前的25个特征下降到2003年后的8个特征。

 

我们将2002年末/ 2003年初月度回报产生过程中独立决定因素的数量和经济重要性的急剧转变，尤其是在公司规模方面，解读为与Shleifer和Vishny(1997)、Lesmond、Schill和Zhou(2004)、Chordia、Roll, and Subrahmanyam (2008)， Li and Zhang (2010)， Lam and Wei(2011)。我们注意到，在2002年7月至2003年6月期间，信息和交易环境发生了一些变化，使得迅速实施定量多/空交易策略的成本更低，技术上更可行。

在2000年10月采用和2001年1月采用十进制报价后，两者都减少了有效价差、价格影响和交易成本(Bessembinder 2003;Eleswarapu, Thompson和V enkataraman 2004)，信息环境在两方面发生了改变。2002年7月，萨班斯-奥克斯利法案(Sarbanes-Oxley Act)通过，该法案增加了审计质量要求，并对公司财务报表的内部控制质量强加了管理责任，从2003年初开始报告的2002财年开始。然后，从2002年11月开始，在财政年度或季度结束后向SEC提交年度和季度报告的最后期限被加快，以使10-Q和10- k报告更及时。

重要的是，从技术角度来看，在2003年1月至5月间，纽约证券交易所推出了自动报价软件，这是亨德肖特，琼斯，和Menkveld(2011)认为，这导致了交易摩擦和成本的大幅减少，同时也大幅增加了做多/做空股票对冲基金用于实施多/做空量化交易策略的算法交易。虽然这些变化的时间融合很难有原因地识别一个或多个解释变化的每月返回生成的过程,我们建议在总更改它便宜得多,技术上更容易迅速实现高容量量化多头/空头交易策略,因此增加了套利活动，提高了股票市场的效率，并且在某种程度上，2003年以前在统计上和经济上显著的特征定价反映了高成本限制的套利，减少了特征的数量和影响决定2003年以后的平均回报。

3.5 稳定性测试

在本节中，我们总结了其他分析的结果，这些分析在互联网附录中详细列出，并评估了我们主要研究结果的稳健性。首先，由于我们的多元方法识别平均收益的独立决定因素是可行的，我们用特征值的标准化平均值替换缺失的特征值的方法(零)，我们重新估计表4而不替换缺失的特征值15我们发现在显著Fama-MacBeth平均斜率系数的身份或数量上几乎没有差异，提供了保证，至少在单变量水平上，而且在仅控制显著基准因子模型的特征版本的水平上，对于任何给定的特征，用标准化的方法替换缺失的值并没有实质性地影响或驱动我们的结果。

其次，鉴于我们在表8和表9中记录的2003年基于特征的收益可预见性的急剧下降，我们分别重新估计了表4的A列中2003年前后的单变量分析。在此过程中，我们证实了2003年基于特征的收益可预见性的下降同时发生在单变量和多变量水平上。我们还确认了我们的发现，基于1980年至2014年的全窗口，也就是说，重要的特征从单变量水平的基本特征转变为多变量水平的主要基于市场的特征，并不仅仅是因为1980-2014年的全窗口数据汇集了2003年前后两个非常不同的子时期的数据。我们观察到，与1980-2014年的整体情况类似，在2003年之前，12个单变量显著特征中有10个是基本特征，而12个独立特征中有2个是基本特征。2003年之后，对比是没有意义的，因为没有单一的显著特征，只有两个独立的特征。

• 由于我们使用对冲收益来评估基于特征的收益可预见性的经济重要性，因此我们确认，我们在表7和表8中报告的对冲收益的大小和重要性，并不是由未能控制共同因素风险所驱动的。我们通过对对冲投资组合回报进行回归，利用了来自Carhart、Fama-French五因素模型和Hou-Xue-Zhang q因素模型的全部94个月因素回报特征。我们还在1990-2002年和2004-2014年期间重复这些测试(未报告)，发现结果与表8报告的结果非常相似。
• 我们使用VWLS和ols分别对大、小和微股的许多回归进行了重新估计。18这些基于规模的互斥分析的结果和推论与我们在本文的主要结果中提出的结果相似。在我们的Internet附录中，我们提供了重叠部分的可视化描述，在这些重叠部分中，特征在不同的回归规范中是重要的，而不是重要的。

3.6 限制

我们认识到我们的研究有几个警告和局限性。虽然我们的研究首次评估了大量个体企业特征的同时预测能力，但迄今为止，我们只研究了异常文献中报告的430多个特征中的四分之一。因此，我们可能不能确定所有真正独立的决定平均月收益的因素。也不适合推断我们的发现430 +的全部人口特征,因为我们的方法是关注那些可以计算从计算机统计程序,或I / B / E / S数据,这意味着我们没有样本随机从公司特征的人口特征。我们可能还引入了测量误差，通过我们处理丢失数据的方法，通过在日历月时间而不是在原始研究中使用的每日或每周时间校准特征。此外，我们注意到，虽然在我们的准样本外测试中，我们试图避免使用实时不可用的数据，但执行我们的对冲投资组合所决定的头寸将使投资者暴露于高交易成本，尤其是在微型股中，这样，交易成本的净对冲回报可能不是正的(Novy-Marx和Velikov 2016年)。

1. 结论和启示

在本文中，我们试图回应Cochrane(2011, 1060)提出的挑战，即研究人员开始识别先前研究中报告的数百个公司特征中的“真实动物园”，其中哪一个是平均股票回报横截面的统计显著预测因子。我们使用与Fama和French在1992年的重要论文相同的方法，但采用了更大的94家公司特征集，并同时将所有94家公司作为解释变量纳入Fama- macbeth回归，以寻求避免过度权重微盘，并针对数据窥探偏差进行调整。我们的方法使我们估计，12个特征提供了从1980年到2014年整个期间非微型股美国平均月收益的重要独立信息，其余82个特征没有提供独立信息。我们表明,一些特征提供独立的信息的原因是独立的决定因素的数量回报本质上是小的,而不是因为少量的特点是能够吸收单变量重要信息在许多其他特征。

我们还证明，独立特征的数量及其产生正对冲回报的能力在2003年急剧下降，尤其是在非微型股中。我们估计，自2003年以来，只有两个特征成为非微盘股回报的独立决定因素，而2003年之前有12个特征，而且2003年之后，非微盘股的平均对冲回报与零没有显著差异。基于特征的可预测性目前只存在于微型股中。我们将公司特征在历法时间和公司规模上数量和经济重要性的下降解释为与Shleifer和Vishny(1997)等人昂贵的限制套利市场效率的论点最一致。

总之，通过确定平均月回报的独立决定因素，并通过放松独立决定因素在公司规模和时间上相同的约束，我们提供了Harvey, Liu，Zhu(2016)、McLean和Pontiff(2016)表示，从数百项回报率异常研究中得出的推论值得怀疑。与此同时，我们也出现了新的事实和困惑，需要消化，其中最突出的是2003年基于特征的回报可预见性的强劲、突然和看似永久的下降，尤其是在非微型股中。我们的结果表明，未来平均收益的实证模型可能受益于对2003年之后数据的权重比2003年之前的数据更强，以及根据公司规模调节收益产生过程，并使用我们确定的(2003年之前与2003年之后)独立的特征作为控制。