最优化方法——QR Factorization

肝！

---

前言

Matrix Inverse
Orthogonal Matrices
前面的两篇blog主要是回顾一下线代知识，打一打基础

这三周学习的QR分解真的又双叕打开了我学习线性代数的格局，总觉得自己的数学真的是太过浅薄，总为那些优美的算法感到惊艳。于是打算整理三篇来好好地捋捋QR分解的理论和实验。（老话重提：不是为了完成DDL而作的blog）

【注】以下内容全部非官方，纯属记录个人角度的理解，如有失偏颇，还望dalao批评指正！

---

一、QR分解

其实就是以计算机判断一个矩阵是否可逆，并求解逆为目的的一种方法。
QR将一个矩阵A分解成具有标准正交列向量的矩阵Q和上三角矩阵R（对角线元素不为0）的算法。这个分解能够有效的提高计算机求解线性方程、最小二乘问题、带约束的最小二乘问题的效率，有效降低计算复杂度。

二、QR分解方法

1.GS QR

Gram-Schmidt QR算法将逐列计算Q和R，通过第k部步的结果推导到第k+1步，类似数学归纳法：

刚开始接触可能会有点儿晕，但是有线代的基础知识的铺垫下，有一些个人理解：
$A=QR$反映的是矩阵A列向量的张成空间与具有标准正交列向量Q的张成空间之间的关系，而且通过QR分解能更直观的得到结论：列向量$q_1,\dots ,q_k$和$a_1,\dots ,a_k$张成的空间相同.
在一组标准正交基下，向量a在某一方向下的投影分量为$q_1^{T}aq$
其实就是利用上面这个结论不断地去掉向量a在已知方向下的投影分量，得到在新的标准正交基下的剩余分量，迭代到终止条件即可。

2.修正的GS QR

GS算法真的给我第一印象十分完美，并为算法的创造者钦佩之至。但是计算机总是个不完美的发明，体现不了数学理论的和谐，由于计算机浮点数存储的舍入误差，会使GS QR在实践的过程中Q矩阵失去正交性，从某个$k$开始，$q_k$与前面的列之间产生了正交性偏差。
修正的GS QR其实也就比GS QR多一句话：对剩余向量进行修正

我实验过程中用GS QR，得到的是如下Q矩阵正交性偏差图：

用修正的GS QR，得到的是如下Q矩阵正交性偏差图：

上图可以反映修改GS QR有更好的数值计算性能，能有效减少计算机浮点数存储的误差。

【关键代码】

% 修正前
for k=1:n_a
    R_a(1:k-1,k)=Q_a(:,1:k-1)'*MatrixA(:,k);
    v=MatrixA(:,k)-Q_a(:,1:k-1)*R_a(1:k-1,k);
    R_a(k,k)=norm(v);
    Q_a(:,k)=v/R_a(k,k);
end

% 修正后
Q_a(:,1)=MatrixA(:,1)/norm(MatrixA(:,1));
for k=2:n_a
    for i=k:n_a
        MatrixA(:,i)=MatrixA(:,i)-MatrixA(:,i)'*Q_a(:,k-1)*Q_a(:,k-1); 
    end
    R_a(k,k)=norm(MatrixA(:,k)); 
    Q_a(:,k)=MatrixA(:,k)/R_a(k,k); 
end

3.Householder

其实上课听这个感觉还挺清楚的，但是课后做实验感觉有点儿顶…
Householder算法是QR分解常用的算法(MATLAB和Julia中的qr函数)，与Gram-Schmidt相比，对舍入误差更有鲁棒性。
$$A=\left[\begin{array}{cc}Q& Q\end{array}\right]\left[\begin{array}{c}R\\ 0\end{array}\right]$$
完整的Q因子被构造成正交矩阵的乘积：
$$[QQ]=H_1{H}_2...H_n$$
每个$H_i\in R^{m\times m}$是对称的正交的“反射算子”

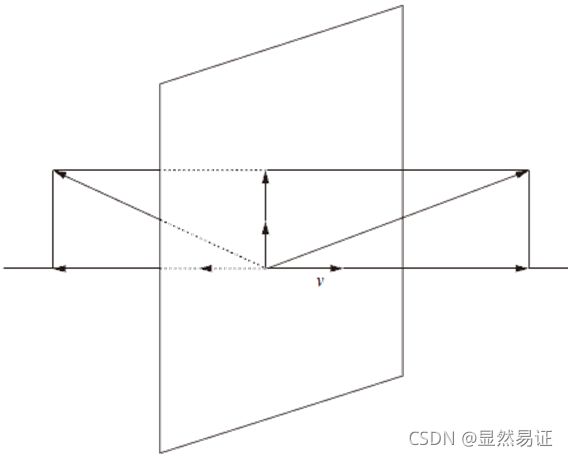
对反射算子的理解，是两个向量关于它们之间垂直平分面的映射，类似“镜面对称”。
它的数学表达式是：$H=I-2v{v}^T$

三角化过程如下：

• R的第一列
  计算将$A$的第一列映射到$e_1$乘积的反射器
  用$I-2v_1{v}_1^T$和$A$的乘积代替$A$
• R的第二列
  计算将$A_{2:4,2}$映射到$e_1$乘积的反射器
  用$I-2v_2{v}_2^T$和$A_{2:4,2:3}$的乘积代替$A_{2:4,2:3}$
• R的第三列
  计算将$A_{3:4,3}$映射到$e_1$乘积的反射器
  用$I-2v_3{v}_3^T$和$A_{3:4,3}$的乘积代替$A_{3:4,3}$
• balabala…其他类似…

【补充】
基于Householder变换也可以证明QR分解的存在性（Q是正交矩阵，R是上三角矩阵）

【关键代码】

for k=1:n_a
    y = MatrixA(k:m_a,k);
    y1 = y(1,1);        
    e1=zeros(m_a-k+1,1);
    e1(1)=1;
    w = y+sign(y1)*norm(y)*e1;
    v=w/norm(w); % 计算反射算子
    MatrixA(k:m_a,k:n_a)=MatrixA(k:m_a,k:n_a)-2*v*(v'*MatrixA(k:m_a,k:n_a));
end
R_a=MatrixA(1:m_a,1:n_a);

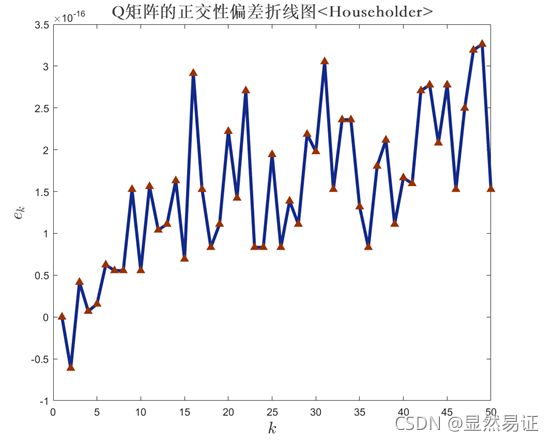
Householder变换确实使矩阵Q的正交性偏差减小，在matlab中还可以调用qr函数，求解Householder QR分解的速度非常快。

% qr函数实现
[Q_a,R_a]=qr(MatrixA);

三、性能比较

算法	性能
Gram-Schmidt算法	复杂度为$2m{n}^2$ flops；在实际情况中不推荐使用(容易被舍入误差影响)
修正Gram–Schmidt算法	复杂度为$2m{n}^2$ flops；有更好的数值计算性能
Householder算法	复杂度为$2m{n}^2-(2/3)n^3$ flops；将$Q$表示为初等正交矩阵的乘积；最广泛使用的算法(在MATLAB和Julia中的qr函数使用该算法)

总结

现在看来好像也不是很晕人了，果然DDL才是干扰理解的罪魁祸首。理解之后，其实两种QR分解的算法无非就是基于三个关键词：”投影“、”映射“和”迭代“。非常有意思的是，两者的出发点不同，一个是利用投影公式不断去掉投影分量（GS）另一个是利用构造反射算子实现对角化，都能实现QR分解，而且数学表达还极其简约√

最后就是总结一下在计算机中怎么求一个矩阵的逆…
这个最优化方法第一节课抛出来的问题…真的好家伙，就衔接上了【哈哈】
当时傻乎乎的觉得应该跟线代里面没啥区别【捂脸】
回归正题：

1. 如何求逆？当然首先是要判断矩阵有没有逆√
   在线代里面是要看最大线性无关组（矩阵是否满秩）或者看矩阵对应的行列式的值是否为0.通过刚刚的QR分解我们可以清楚的知道，奇异矩阵是不能进行QR分解的，判断条件可以设置为R矩阵对角线元素是否为0，若存在为0的对角线元素则奇异；否则非奇异，也就是说我们可以去求它的逆。
2. 如何根据QR分解去求逆？
   手推如下：
   

That’s all！Bye~
码字不易，记得点赞+关注+收藏+好评(๑•̀ㅂ•́)و✧