自回归模型AR(p)的python实现【案例】
目录
1. AR模型
2. statsmodels.tsa.ar_model
3. 示例:
4. matplotlib查看模型预测结果
1. AR模型
时间序列数据通常可由历史数据的加权和与随机扰动的叠加来表示,p阶自回归模型的形式为:
式中![]() 为常系数,
为常系数,![]() 为随机扰动(噪声)项。
为随机扰动(噪声)项。
假设![]() 为白噪声
为白噪声![]() ,则自回归模型存在平稳解,稳定的差分方程系统称为AR(p)模型。
,则自回归模型存在平稳解,稳定的差分方程系统称为AR(p)模型。
2. statsmodels.tsa.ar_model
python中用statsmodels.tsa.ar_model包中的AutoReg来实现自回归。
官网函数介绍:
statsmodels.tsa.ar_model — statsmodels
调用语句:
from statsmodels.tsa.ar_model import AutoReg
ar_model = AutoReg(endog, lags, trend='c', seasonal=False, exog=None, hold_back=None, period=None, missing='none', *, deterministic=None, old_names=False)
# 通常只需要两个参数
ar_model = AutoReg(timeseries, lags)通常情况下只需要输入序列endog和阶数lags:
endog:一维时间序列
lags:模型阶数,可取lags=None(0阶),lags=[1, 4] 将仅包括滞后 1 和 4(![]() ),而 lags=4 将包括滞后 1、2、3 和 4(
),而 lags=4 将包括滞后 1、2、3 和 4(![]() )。
)。
3. 示例:
from statsmodels.tsa.ar_model import AutoReg
import numpy as np
# 生成N(0,1)随机正态分布(白噪声)
noise = np.random.randn(200)
wnoise = (noise-np.mean(noise))/np.std(noise)
# 生成AR(2)线性序列 X(t)=0.5X(t-1)+0.1X(t-2)
X = [20,10] # 初值
for i in range(200):
x2 = 0.5*X[i+1]+0.1*X[i]+wnoise[i]
X.append(x2)
# 2阶AR模型拟合(OLS)
AR2_model = AutoReg(X, 2).fit()
# 模型预测第3到第202个时间点的数据
predict = AR2_model.predict(2,201)
# 计算残差
residual = X[2:]-predict4. matplotlib查看模型预测结果
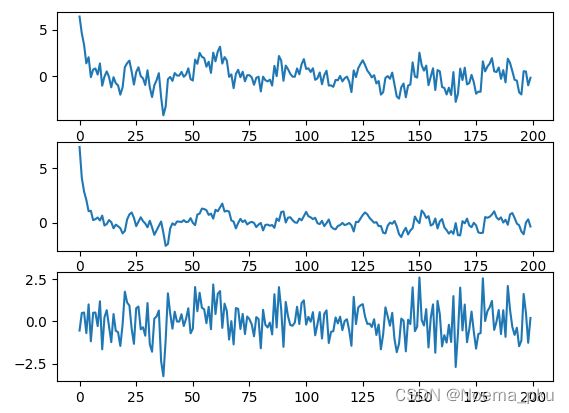
import matplotlib.pyplot as plt
plt.figure()
plt.subplot(311)
plt.plot(X[2:])
plt.subplot(312)
plt.plot(predict)
plt.subplot(313)
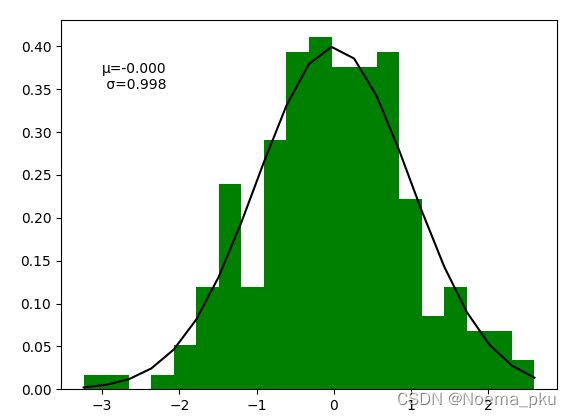
plt.plot(residual)残差仍然为N(0,1)的白噪声:
# 查看残差的分布
import scipy.stats as st # 统计分析库
plt.figure()
n, bins, patches = plt.hist(residual,20, density=True, histtype='bar', facecolor='green')
power_mean = np.mean(residual) # 均值约为0
power_std = np.std(residual) # 方差约为1
y = st.norm.pdf(bins, power_mean, power_std) # 拟合PDF
plt.plot(bins, y, color='k')
plt.text(-3,0.35,'μ='+'%.3f' %power_mean+'\n σ='+'%.3f' %power_std)
预测成功!