Matplotlib和Seaborn(饼图,直方图)
文章目录
- 饼图
- 直方图
-
- 其他方法
饼图
饼图是一种常见的单变量图表,用于描绘分类变量各类别的相对频率。饼图中的扇区代表频率大小;角度或面积越大,该类别就出现地越频繁。

遗憾的是,饼图是一种应用场合很有限的图表类型,图表创建者很容易将饼图绘制得难以看懂。如果你要使用饼图,请尝试遵守下面的规则:
- 确保你关心的是相对频率。每个扇区应该表示整体的一部分,而不是单独的数值(除非变量能够求和成某个整体)。
- 将扇区限制在一定数量内。饼图最好只包含两到三个扇区,如果扇区足以明确区分,也可以包含四到五个。如果你有很多个类别,并且某些类别所占的比例很小,那可以将它们组合到一起,或者将这些比例很小的类别放到 “其他” 类别中。
- 系统地绘制数据。绘制饼图的一种常见方法是从圆圈的顶部开始,然后沿着顺时针方向绘制每个分类级别,从最常见的到最不常见的排列。如果有三个类别,并且想要对比其中两个,一种常见绘制方法是将这两个类别放在 12 点钟方向的两侧,第三个类别填充在底部剩余部分。
如果无法满足这些规则,则建议使用条形图。通常选择条形图更保险。长条高度比面积或角度更精确,并且条形图比饼图更紧凑。对于值很多的变量来说,条形图更灵活。
你可以使用 matplotlib 的 pie 函数创建饼图。此函数需要数据为汇总的形式:函数的主要参数是扇区大小 。
# code for the pie chart seen above
sorted_counts = df['cat_var'].value_counts()
plt.pie(sorted_counts, labels = sorted_counts.index, startangle = 90,
counterclock = False);
plt.axis('square')
为了遵守上面提到的规则,我们可以添加 “startangle = 90” 和 "counterclock = False"这两个参数,在垂直上方开始第一个扇区,然后按照顺时针方向有序地绘制每个扇区。axis 函数的使用和 "square" 参数的设定, 将使 x 和 y 轴的长度相等。不调用此函数的话,最终的图形可能看起来更像椭圆而不是正圆。
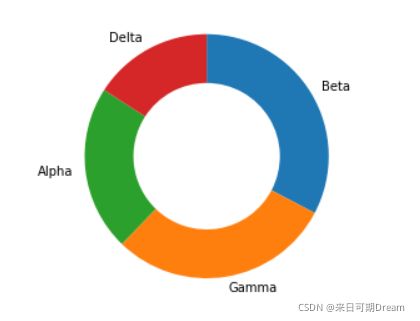
饼图的一种变体形式是环形图。它看起来很像饼图,但是图形中间有个洞。从视觉感知上来看,环形图和饼图没有什么太大的区别,所以应该按照饼图的相同规则使用环形图。选择饼图还是环形图的原因之一可能是看起来是否美观。比如,你可能会在一些报告中看到,在环形图中间的空白处展示一些统计数据,充分利用空间。
要创建环形图,可以在 pie 函数调用中添加 "wedgeprops" 参数。默认情况下,饼图(圆形)的半径是 1;将扇区宽度属性设为小于 1 的值会删除圆形中心的颜色。
直方图
直方图用来绘制数值变量的分布情况。它是条形图的数值变量版本。但是,我们不会为每个单独的数值绘制一个长条,而是定义几个连续的分组(bin),为每个分组绘制长条以代表相应的数字。例如,使用 matplotlib 的 hist 函数的默认设置:
plt.hist(data = df, x = 'num_var')
可以看出,最左侧的分组(约为 0 到 2.5 之间)包含 8 个数据点,其相邻的分组 (约为 2.5 到 5 之间)包含 9 个数据点。总体来说,可以看出是一个双峰分布。直方图中的长条彼此相连,而条形图中的长条是分开的,表明在直方图中数据的值处在连续范围内。如果某个数值位于分组的边界,则属于右侧的分组。例外情况是最右侧的分组边界,将上限值放入了最右侧的分组内(上限值的左侧分组)。
默认情况下,hist 函数会根据值的范围将数据分成 10 个组。在几乎所有情况下,我们都需要更改这一设置。因为,10 组一般来说都太少了,无法了解数据真实的分布情况。并且默认的刻度都不太好解释,没有“四舍五入”到某个具体的好描述的值。如果在上述示例中,将“约为0 到 2.5 之间”改为“0 到 2.5 之间”,将“约为2.5 到 5 之间”改为“2.5 到 5 之间”,是不是更方便?
你可以使用描述统计量(例如通过 df['num_var'].describe())估计什么样的组下限和组上限最合适。可以使用 numpy 的 arange 函数设置这些分组的边界:
bin_edges = np.arange(0, df['num_var'].max()+1, 1)
plt.hist(data = df, x = 'num_var', bins = bin_edges)
arange 的第一个参数是最左侧的分组边界,第二个参数是上限值,第三个参数是组距(bin width)。注意,即使已经在第二个参数中指定了最大值,我又给这个值 “+1” 了。这是因为 arange 仅返回完全小于上限的值。“+1” 可有效地确保最右侧的分组边界至少是数据的最大值,以便所有数据点都能绘制出来。最左侧的分组设为硬编码的 0,以便获得更好解释的边界数值,当然你也可以使用 numpy 的 around 等函数以编程方式达到这种效果。

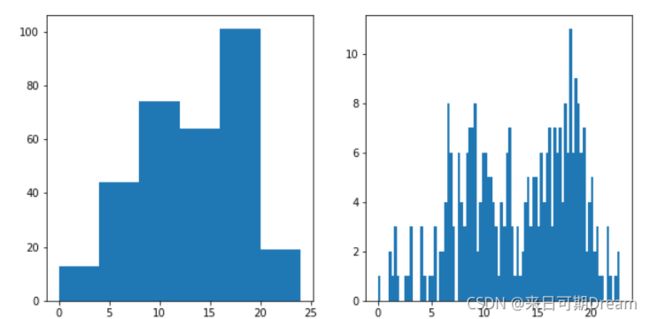
在创建直方图时,有必要尝试不同的组距,看看哪个组距最能表示数据。如果组太多,可能会发现太多噪点,干扰我们发现数据里蕴含的规律。如果组太少,则根本无法看出真正的规律。
plt.figure(figsize = [10, 5]) # larger figure size for subplots
# histogram on left, example of too-large bin size
plt.subplot(1, 2, 1) # 1 row, 2 cols, subplot 1
bin_edges = np.arange(0, df['num_var'].max()+4, 4)
plt.hist(data = df, x = 'num_var', bins = bin_edges)
# histogram on right, example of too-small bin size
plt.subplot(1, 2, 2) # 1 row, 2 cols, subplot 2
bin_edges = np.arange(0, df['num_var'].max()+1/4, 1/4)
plt.hist(data = df, x = 'num_var', bins = bin_edges)
该示例通过 subplot 函数将两个图表并排地放到一起,函数的参数指定了子图的行数、列数和索引。figure() 函数在调用时传入了 “figsize” 参数,绘制尺寸更大的图纸,以便其中可以包含更多的子图。
其他方法
seaborn 函数 distplot 也可以用于绘制直方图,该函数集成了一些其他的单变量绘图函数
sb.distplot(df['num_var'])
注意,第一个参数_必须_是 Series 或数组,其中包含要绘制的数据点。这与我们之前看到的 countplot 和 hist 函数不同,后面两个函数需要分别指定数据源和列两个参数。
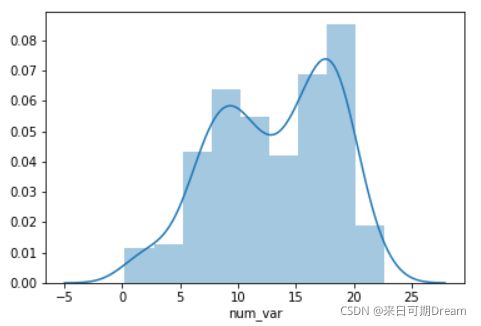
distplot 函数具有绘制直方图的内置规则,默认情况下,会在数据上绘制一个 核密度估计(KDE)。纵轴基于 KDE,而不是直方图:长条的高度之和不一定等于 1,但是曲线下方的面积应该等于 1。如果你想详细了解 KDE,请参阅这节课最后 的补充内容。
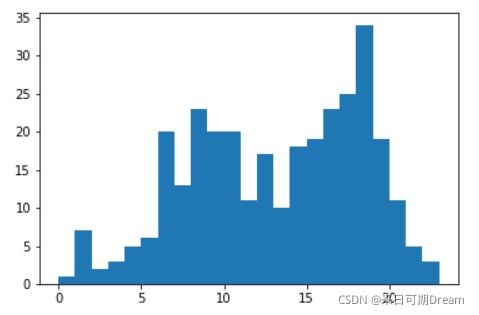
虽然默认的 distplot 的分组形式比 .hist 固定的 10 个分组更好,但是你依然可能需要对它进行调整,使分组的边界值为“四舍五入”后的值。你可以使用其他参数自定义直方图,或者像之前那样指定分组:
bin_edges = np.arange(0, df['num_var'].max()+1, 1)
sb.distplot(df['num_var'], bins = bin_edges, kde = False,
hist_kws = {'alpha' : 1})
alpha(透明度)的设置必须在参数 “hist_kws” 的字典里,因为还有其他底层绘图函数(例如 KDE)具有自己的可选关键字参数。
总之,如果你只想了解数据的直方图分布情况,而不想要 distplot 提供的额外信息,为了简便,建议只使用 Matplotlib 的 hist 函数。另一方面,如果你想快速了解如何为直方图选择代表性的分组组距,建议在自定义之前,先快速查看下 一下distplot。