细读Autoformer—空间计量分析
文章目录
- 摘要
- 一. 细读Autoformer
-
- 1.1 论文摘要
- 1.2 研究内容
- 1.3 Autoformer模型框架
-
- 1.3.1 Series Decomp Block
- 1.3.2 Model inputs
- 1.3.3 Encoder
- 1.3.4 Decoder
- 1.3.5 Auto-Correlation Mechanism
- 二. 空间计量分析理论部分
-
- 2.1 空间计量经济学概述
- 2.2 空间权重矩阵得设定与选择
-
- 2.2.1 空间权重矩阵的设定
- 2.2.2 如何选择合适的空间权重矩阵
- 2.2.3 空间权重矩阵的标准化处理
- 2.3 空间自相关检验
-
- 2.3.1 全局莫兰指数与局部莫兰指数
- 2.4 空间计量模型得设定与选择
-
- 2.4.1 空间计量模型
- 2.4.2 如何去选择合适的空间模型
- 三. pytorch框架基础
-
- 3.1 nn.Model
- 3.2 CONV2D 是如何计算的
- 3.3 卷积层的具体简单代码实现
- 3.4 查看VGG16 model 卷积神经网络怎么去写
- 3.5 Pooling layer MaxPool2(最大池化的作用)
- 3.6 非线性激活操作Non-Linear Activations
- 3.7 线性层网络
- 3.8 神经网络实战小举例
- 毕设
- 总结
摘要
本周一是重新细读了Autoformer模型,对Autoformer的组成部分:序列分解模块(decompostion block),自相关机制(Auto-Correlation mechanism),编码和解码器(Encoder和Decoder),其输入输出有着详细理解。尤其是该论文的自相关机制如何去取代原来的自注意力机制,以及结合长时间预测的实际需要,说明了为什么需要这样做与自相关机制的独特优势。
二是对空间计量分析相关的理论部分进行了较为系统的学习,从空间计量概述,到空间权重矩阵的介绍与设定,以及应该如何选择;再到空间自相关检验莫兰指数等的公式介绍;以及空间计量模型的介绍与设定,如何去选择一个合适需求的计量模型。
三是对 pytorch框架基础的简单实践,都是基础内容。
一. 细读Autoformer
1.1 论文摘要
本文研究时间序列的长期预测问题,先前基于Transformer的模型都是采用各种自我注意机制来发现长期依赖关系,但对于长期预测来说表现并不是很好,难以发现可靠的依赖关系。并却由于Transformer都必须采用逐点稀疏版的self-attention以提高长序列效率,从而导致信息利用缺失。该文提出的Autoformer 设计为一种具有自相关机制的新型分解架构。该模型的大体框架是与Transformer相似的,但是Autoformer尝试将分解序列和预测序列都合在一个模型里面看,新添加了decomposition block序列分解模块,与用Auto-Correlation去替代自注意力机制。
1.2 研究内容
本文主要探索长期时间序列预测问题:待预测的序列长度(O)远远大于输入长度(I),即基于有限的信息预测更长远的未来。对于长时间预测来说,模型的预测能力及计算效率有着很强的要求。然而Transformer在长序列的 O ( L 2 ) O(L^2) O(L2)时间复杂模式下很难发现可靠的时序依赖;基于Transformer的改进模型主要着力于稀疏注意力特征图 ( Q K T QK^T QKT) 来降低模型复杂度,而这些模型仍使用以节点为最小单位进行消息汇聚,这样将造成信息的丢失,这成为了长时间时序预测的性能瓶颈。
为了突破之前的困境,Autoformer的模型将从序列分解出发,提出Auto-Correlation机制替代self-attention,其考虑sub-series(子序列)间的相似度能更好的捕捉到趋势性,更多的关注序列,而不是节点。不仅要保证时间复杂度,也需要防止信息的丢失。
1.3 Autoformer模型框架
Autoformer主要由三部分组成:
● 序列分解模块(decompostion block);
● 自相关机制(Auto-Correlation mechanism);
● 编码和解码器(Encoder和Decoder)。

编码解码架构同时由Auto-Correlation、Series Decomp、Feed Forward三个模块组成每一层,同时使用残差结构。因为模型的输入会用的Series Decomp Block,因此先介绍这个模块。
1.3.1 Series Decomp Block
Series Decomp Block使用传统的decomposition分解操作可以将序列分解为trend趋势项和seasonal季节项这两个部分,关于这两个部分的理解是一个可以反应短期的波动另一个则反应长期的季节性。
其中padding是为了保证序列长度不变,avgpool是移动平均。获取趋势项后,序列-趋势=季节。

X t X_t Xt存储的是每个滑动窗口的均值,而 X s X_s Xs则是保留季节性的平滑序列。
1.3.2 Model inputs
编码器的输入为已知历史 I I I个时间点长度的序列,解码器的输入包括季节项 和周期项 ;一个是季节项 [ X d e s ∈ R ( I / 2 + O ) ∗ d X_{des}\in\R^{(I/2+O)*d} Xdes∈R(I/2+O)∗d],另一个是周期项[ X d e t ∈ R ( I / 2 + O ) ∗ d X_{det}\in\R^{(I/2+O)*d} Xdet∈R(I/2+O)∗d]。前 I / 2 I/2 I/2 部分由 X e n X_{en} Xen 分解得到,后面的 O O O长度序列分别由0与均值mean补齐。d为时序条数,O为未来时间长度。
公式表示如下:


上图来源知乎机器学习社区,上图清晰的反应了编码器与解码器的输入。
1.3.3 Encoder
关注季节部分建模的编码器,输出的是过去季节性信息,它将被用做互信息,帮助解码器调整预测结果。只保留平滑的seasonal part, 每一层的处理公式如下:

假设我们有 N 个编码器层。 第 l 个编码器层的整体方程总结为:
![]()
1.3.4 Decoder
假设我们有M个解码层,第l个解码层 的内部细节如下;
解码器包括两个部分:
● 上路是对seasonal季节项成分使用堆叠自相关机制;
● 对trend-cyclical周期项成分使用累加操作。

对于季节项,自相关机制利用序列的周期性质,聚合不同周期中具有相似过程的子序列;对于趋势项,使用权重累积的方式,逐步从预测的隐变量中提取出趋势信息。。其中, [ X e n N X_{en}^N XenN] 是encoder中的潜在变量,第l个decoder layer的方程可以看作 X d e l = D e c o d e r ( X d e l − 1 ) , X e n N ) X_{de}^l=Decoder(X_{de}^{l-1}),X_{en}^N) Xdel=Decoder(Xdel−1),XenN) 。
模型最终的输出结果为:
![]()
1.3.5 Auto-Correlation Mechanism
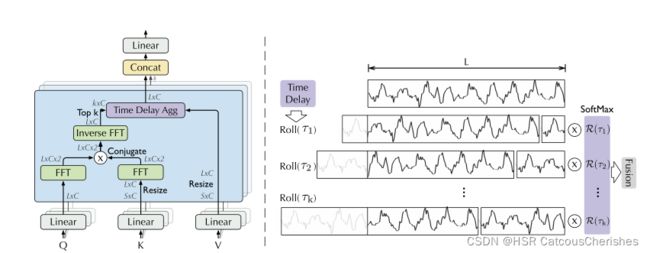
自相关机制模块关键是如何高效计算自相关系数:通过计算序列自相关系数,发现周期依赖项(Period-based dependencies),然后再平移时间做相似子序列的聚合(Time delay aggregation)。
如上图所示,Q,K,V和Transformer一样通过映射输入得到,首先注意到对Q和K分别执行快速傅里叶变换操作 (FFT),K还执行了共轭操作,公式如下(基于Wiener–Khinchin theorem ):
τ τ τ 是从1取到L,然后分别算出前K个最大的TOPK,取为K个 τ 1 , . . . . . τ k τ_1,.....τ_k τ1,.....τk做周期长度。
当使用FFT高效求解出 τ τ τ 从 1 1 1 到 L − 1 L-1 L−1 的所有 R X X ( T ) R_{XX}(T) RXX(T) 后,然后本文将只取出最大的 t o p k top k topk 个 R X X ( T ) R_{XX}(T) RXX(T),并且对取出的 k k k个 R X X ( T ) R_{XX}(T) RXX(T)执行 s o f t m a x softmax softmax 操作转换为概率,最后将 k k k个概率与对应的进行 R O L L ( ) ROLL() ROLL()操作之后的 V V V 相乘后相加得到最后的结果,如下所示:

其中 R O L L ( ) ROLL() ROLL()操作是将 V V V 按相同相位移动(前面得部分移动到后面对齐),具体图解如下:
二. 空间计量分析理论部分
2.1 空间计量经济学概述
所谓空间数据,就是在原来得横截面或者面板数据上,加上横截面单位的位置信息(或者相互距离)。研究如何处理空间数据的计量经济学分支,称为“空间计量经济学”。
传统的计量只是研究了个体的自变量对个体的因变量的影响,而空间计量在传统计量的基础上,进一步研究个体的自变量对其他个体的因变量的影响。因此空间计量经济学最大的特色在于充分考虑横截面单位(地理区域)之间的空间依赖性。
空间相关性,也称空间依赖性,是指不同区域的事物和现象之间在空间上的互相依赖、互相制约、互相影响和互相作用,是事物和现象本身固有的空间经济属性,是地理空间现象和空间过程的本质属性。
空间依赖可以定义为观测值及区位之间的依赖性。当相邻区域特征变量的高值或低值在空间上呈现集聚倾向时为正的空间自相关,反之,当相邻区域特征变量取值与本区域变量取值高低相反时则为负的空间自相关。
为什么会存在空间相关性!
原因1:观测数据地理位置邻近
原因2:截面层个体的相互竞争与合作
原因3: 模仿行为
原因4:溢出效应
原因5:测量误差
2.2 空间权重矩阵得设定与选择
如何将经济变量的空间效应纳入回归方程中,这便需要根据某种标准建立空间权重矩阵。
2.2.1 空间权重矩阵的设定
之前也学习了三种空间权重矩阵,还有一个综合距离,以及它们应该如何去获取与创建。下面再简单复习一下:
一般的经济指标是应用人均GDP,再按如下的公式去计算经济距离矩阵:

对于如何创建经济距离权重矩阵,在之前的文章中有相关介绍。
- 综合距离矩阵

由于选取的距离形式不同,对于空间相似度的度量也会造成不同的结果。所以需要根据不同的需求,对距离进行加权处理。但具体怎么做还不是很清楚?
2.2.2 如何选择合适的空间权重矩阵
尽管二进制的空间邻近权值矩阵并非适用于所有的空间计量经济模型,但是,处于某些情况下的实用性,在构建空间计量模型时的首选就是从二进制的邻近矩阵开始的。
一般是先从空间邻近的最基本二进制矩阵开始,逐步选择确定空间权值。
关于各种权值矩阵的选择,没有现成的理论根据,一般可考虑空间计量模型对各种空间权值矩阵的适用程度,检验估计结果对权值矩阵的敏感性,最终的依据实际上就是结果的客观性和科学性。
2.2.3 空间权重矩阵的标准化处理
下面说明一下需要标准化的原因,以及处理的公式:


空间权重矩阵标准化的优缺点:
具体执行过程在Stata软件分析中使用代码可轻松实现这一操作。
2.3 空间自相关检验
在确定好空间权重矩阵之后,我们需要对判断数据做是否存在空间自相关性。
“空间自相关”可以理解为位置相近的区域具有相似的变量取值。如果高值与高值集聚在一起,低值与低值集聚在一起,则为“正空间自相关”;反之,如果高值与低值相邻,则为“负空间自相关”;如果高值与低值完全随机地分布,则不存在空间自相关。
目前常用来考察数据空间自相关的指标为莫兰指数I和吉尔里指数C,其中莫兰指数是最常用的。
2.3.1 全局莫兰指数与局部莫兰指数

莫兰指数I如果接近于0,则说明该空间分布是随机的,不存在空间自相关。

它们的具体实现,之前也有demo做了执行代码,结果展示,这里是再次理清它们的概念与判断。
2.4 空间计量模型得设定与选择
2.4.1 空间计量模型
再次理解一下空间计量模型表示与含义:
1. SAR
在空间自回归模型(空间滞后模型)中,被解释变量间存在较强的空间依赖性,进而邻地被解释变量会通过空间传导机制影响到本地的被解释变量。(比如技术扩散)
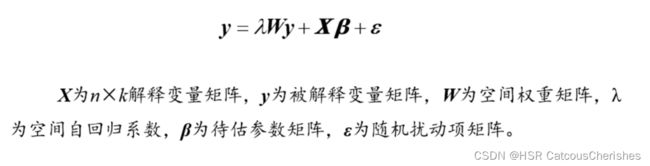
2.SEM
2.4.2 如何去选择合适的空间模型
对一般性空间计量模型进行拉格朗日乘数检验**(LM检验**)、稳健的拉格朗日乘数检验(RLM检验)和似然比检验(LR检验),根据检验结果来选择合适的模型。
具体过程可参考空间计量领域经典论文:如【中国东部沿海五大城市创新效率,影响因素及空间溢出效应】
三. pytorch框架基础
3.1 nn.Model
神经网络的基本骨架-nn.Module
import torch
from torch import nn
class Tudui(nn.Module):
def __init__(self):
super(Tudui, self).__init__()
## 调用父类初始化函数
def forward(self,input):
output = input+1 # 最简单的自定义
return output ## 自定义输出
y=Tudui() # 实例化类
x = torch.tensor(1.1) # 注意: Tensor是class,tensor是function,将数据类型转换为Tensor
output = y(x)
print(output)
# tensor(2.1000)
3.2 CONV2D 是如何计算的
详细计算过程可见:torch.nn.functional.conv卷积模块详解模块
torch.nn.functional.conv2d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1) → Tensor
functional.conv2d函数的使用
import torch
import torch.nn.functional as F
# 输入:5x5矩阵
input = torch.tensor([[1, 2, 0, 3, 1],
[0, 1, 2, 3, 1],
[1, 2, 1, 0, 0],
[5, 2, 3, 1, 1],
[2, 1, 0, 1, 1]])
# 卷积核3x3矩阵
kernel = torch.tensor([[1, 2, 1],
[0, 1, 0],
[2, 1, 0]])
# 尺寸变换,要对应conv2d input的要求(minibatch=1,channel=1,h,w)
input = torch.reshape(input, (1, 1, 5, 5))
kernel = torch.reshape(kernel, (1, 1, 3, 3))
# stride:每次(在哪个方向)移动几步
output = F.conv2d(input, kernel, stride=1)
print(output)
output1 = F.conv2d(input, kernel, stride=2)
print(output1)
output2 = F.conv2d(input, kernel, stride=1, padding=1) # padding=1是一般默认为全零填充一圈
print(output2)
# output
# tensor([[[[10, 12, 12],
# [18, 16, 16],
# [13, 9, 3]]]])
# tensor([[[[10, 12],
# [13, 3]]]])
# tensor([[[[ 1, 3, 4, 10, 8],
# [ 5, 10, 12, 12, 6],
# [ 7, 18, 16, 16, 8],
# [11, 13, 9, 3, 4],
# [14, 13, 9, 7, 4]]]])
3.3 卷积层的具体简单代码实现
GitHub上可视化卷积过程 卷积层动图理解(蓝色input,绿色output,深色kernel)。
dilation:设置了的话就是空洞卷积(可见上面链接中的可视化)。
#CLASS torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)
# 卷积层的具体代码实现
# 先理解参数:
# in_channels (int) – 输入图像中的通道数
#
# out_channels (int) – 卷积产生的通道数
#
# kernel_size (int 或元组) – 卷积核的大小(3代表3*3,或者(1,2)
#
# stride (int 或元组,可选) – 卷积的步幅。默认值:1
#
# padding(int、元组或 str,可选) – 填充添加到输入的所有四个边。默认值:0
#
# padding_mode (字符串, 可选) – , , 或 .违约:'zeros''reflect''replicate''circular''zeros'
#
# dilation(int或元组,可选)——核元素之间的间距。默认值:1
#
# groups(int,可选) – 从输入通道到输出通道的阻塞连接数。默认值:1
#
# bais(bool,可选) – 如果 ,向输出添加一个可学习的偏差。默认:TrueTrue
import torch
import torchvision
from torch import nn
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
dataset = torchvision.datasets.CIFAR10("./dataset", train=False, transform=torchvision.transforms.ToTensor(),
download=True)
dataloader = DataLoader(dataset=dataset, batch_size=64, shuffle=True, drop_last=False)
class test(nn.Module):
def __init__(self):
super(test, self).__init__()
self.conv1 = nn.Conv2d(in_channels=3, out_channels=6, kernel_size=3, stride=1, padding=0) ## 注意这里必须配置正确nn.Conv2d()
def forward(self, x):
x = self.conv1(x)
return x
writer = SummaryWriter("../log1")
test1 = test()
step = 0
for data in dataloader:
imgs, t = data
output = test1(imgs)
print(imgs.shape)
# torch.size([64,3,32,32]) ([B,C,H,W])
print(output.shape)
# torch.Size([64, 6, 30, 30])
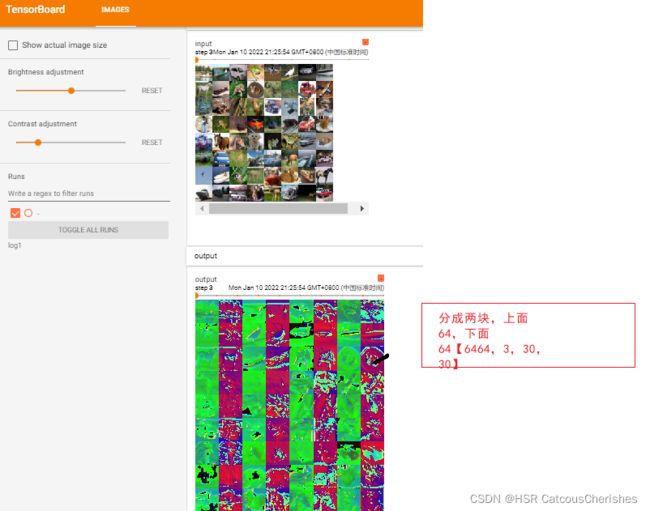
writer.add_images("input", imgs, step)
# 由于图片只能以三个通道显示,因此要把6个channel改成3个
# torch.size([64,6,30,30])->[???,3,30,30]
# 注意这个 batch_size不知道写多少的时候就写-1,它会自动计算
output = torch.reshape(output, (-1, 3, 30, 30))
## 需要转换shape(如上)
writer.add_images("output", output, step)
step = step + 1
writer.close()
## 查看VGG16 model 卷积神经网络怎么去写
3.4 查看VGG16 model 卷积神经网络怎么去写
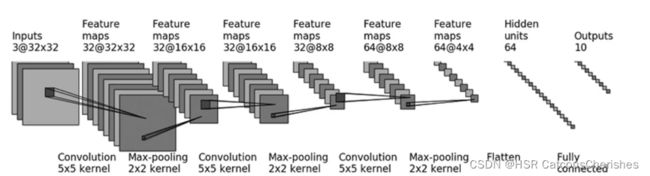
如下图一个经典案例:
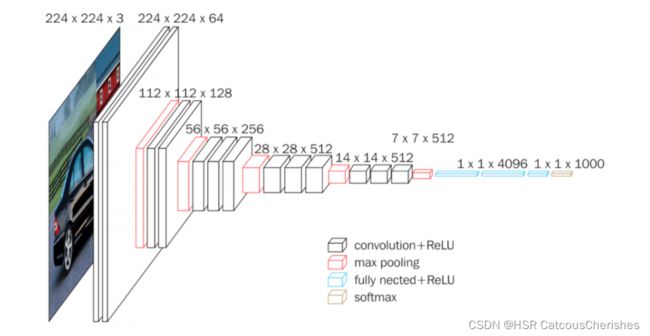
可见其input是 3通道,224224;然而其卷积之后是(224224*64),可知是维持了图片的尺寸,定是padding 进行了填充,所以我们可以将 【上个案例中卷积操作:nn.Conv2d(in_channels=3, out_channels=6, kernel_size=3, stride=1, padding=0)】
那么本图中可知:(in_channels=3,out_channels=64,…)

由上面公式可推导出padding 等参数。
3.5 Pooling layer MaxPool2(最大池化的作用)
上官网查看具体的知识:Maxpooling
参数有:
kernel_size – 窗口的大小,以达到最大值
stride – 移动窗户的步幅。默认值为kernel_size
padding– 要在两侧添加的隐式零填充
dilation– 控制窗口中元素步幅的参数(空洞卷积)
return_indices – if 将返回最大指数和输出。对torch.nn.MaxUnpool2d稍后有用True
ceil_mode – 当为 True 时,将使用ceil而不是floor来计算输出形状(ceil向上取整,floor向下取整)
import torch
import torchvision
from torch import nn
from torch.nn import MaxPool2d
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
dataset = torchvision.datasets.CIFAR10("./dataset", train=False, transform=torchvision.transforms.ToTensor(),
download=True)
dataloader = DataLoader(dataset=dataset, batch_size=64, shuffle=True, drop_last=False)
# #输入:5x5矩阵
# input=torch.tensor([[1,2,0,3,1],
# [0,1,2,3,1],
# [1,2,1,0,0],
# [5,2,3,1,1],
# [2,1,0,1,1]],dtype=torch.float32) #dtype:将数据类型更改为浮点数
# ## 由于方法规定,必须转换形状
# input=torch.reshape(input,(-1,1,5,5))
# print(input.shape)
class Test(nn.Module):
def __init__(self):
super(Test, self).__init__()
self.maxpool1 = MaxPool2d(kernel_size=3,ceil_mode=True)
self.maxpool2 = MaxPool2d(kernel_size=3,ceil_mode=False)
def forward(self,input):
output1 = self.maxpool1(input)
output2 = self.maxpool2(input)
# return output1
return output1,output2
test = Test()
# 与之前的input 对应输出
# output = test(input)
# print(output)
# 输出结果 两种情况
# (tensor([[[[2., 3.],
# [5., 1.]]]]), tensor([[[[2.]]]]))
writer = SummaryWriter("../log1")
step= 0
for data in dataloader:
imgs,targets = data
writer.add_images("input",imgs,step)
# 注意,最大池化不会改变channel(input是3通道,output也是3通道)
output1,output2 = test(imgs)
writer.add_images("output1",output1,step)
writer.add_images("output2",output2,step)
step=step+1
writer.close()
输出池化之后的结果图片:

最大池化的作用:在保留原有数据特征的情况下 减小数据量。
3.6 非线性激活操作Non-Linear Activations
看官方文档:官方非线性激活文档
import torchvision
from torch import nn
from torch.nn import ReLU, Sigmoid
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
dataset = torchvision.datasets.CIFAR10("./dataset", train=False, transform=torchvision.transforms.ToTensor(),
download=True)
dataloader = DataLoader(dataset=dataset, batch_size=64, shuffle=True, drop_last=False)
class test(nn.Module):
def __init__(self):
super(test, self).__init__()
# inplace:是否将 input 替换成output (一般默认为False,不会取代原来的input)
self.relu1 = ReLU(inplace=False)
self.sigmoid1 = Sigmoid()
def forward(self, input):
output = self.relu1(input)
output = self.sigmoid1(output)
return output
test1 = test()
writer = SummaryWriter("../log1")
step = 0 # 每一个循环是一个batch=64,drop_last为False是不舍弃不足的
for data in dataloader:
imgs, t = data
writer.add_images("input", imgs, step)
output = test1(imgs)
writer.add_images("output", output, step)
step = step + 1
writer.close()
经过ReLU与Sigmoid非线性激活的操作后:

非线性激活的作用是:提升模型的泛化能力
3.7 线性层网络
正则化的官方文档:BATCHNORM2D
查看官网线性层的文档: Linear Layers
torch.nn.Linear(in_features, out_features, bias=True, device=None, dtype=None)
-
in_features – 每个输入样本的大小
-
out_features – 每个输出样本的大小
-
bias – If set to False, the layer will not learn an additive bias. Default: True
下面是经典的VGG16 model :
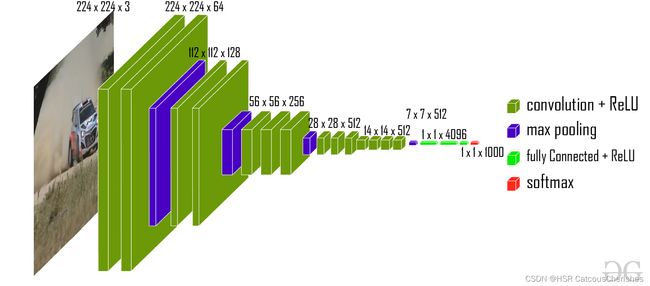
可见图上后两层是由( 1 ∗ 1 ∗ 4096 1*1*4096 1∗1∗4096)–线性层->( 1 ∗ 1 ∗ 1000 1*1*1000 1∗1∗1000),那这里是如何实现的?
线性层的简单实现:
import torch
import torchvision
from torch import nn
from torch.nn import Linear
from torch.utils.data import DataLoader
dataset = torchvision.datasets.CIFAR10("./dataset", train=False, transform=torchvision.transforms.ToTensor(),
download=True)
# 这里不droplast=True 后面会报错,因为linear1的定义是 196608,而最后一组图片不够64张, 最后的大小也不足 196608
dataloader = DataLoader(dataset, batch_size=64, drop_last=True)
class test(nn.Module):
def __init__(self):
super(test, self).__init__()
self.linear1 = Linear(196608, 10) ## 线性层(输入 feature,输出 feature)
def forward(self, input):
output = self.linear1(input)
return output
test1 = test()
for data in dataloader:
imgs, t = data
print(imgs.shape)
# 将图片线性化
output = torch.reshape(imgs, (1, 1, 1, -1))
# flatten也可以用
#output=torch.flatten(imgs)
print(output.shape)
output = test1(output) # 经过linear层之后变成10维
print(output.shape)
# torch.Size([64, 3, 32, 32])
#torch.Size([1, 1, 1, 196608])
# torch.Size([1, 1, 1, 10])
3.8 神经网络实战小举例
我们应用CIFAR10数据集做一个十分简单的分类,根据图片的内容识别属于哪一个类即可。
import torch
from torch import nn
class test(nn.Module):
def __init__(self):
super(test, self).__init__()
#因为size_in和size_out都是32,经过计算得出padding=2,stride=1
self.conv1=nn.Conv2d(3,32,5,padding=2,stride=1)
self.pool1=nn.MaxPool2d(2)
#尺寸不变,和上面一样
self.conv2=nn.Conv2d(32,32,5,stride=1,padding=2)
self.pool2=nn.MaxPool2d(2)
# 尺寸不变,和上面一样
self.conv3=nn.Conv2d(32,64,5,stride=1,padding=2)
self.pool3 = nn.MaxPool2d(2)
self.flatten=nn.Flatten()
#in_feature:64*4*4,out_feature:64
self.linear1=nn.Linear(1024,64)
self.linear2=nn.Linear(64,10)
def forward(self,x):
x=self.conv1(x)
x = self.pool1(x)
x = self.conv2(x)
x = self.pool2(x)
x = self.conv3(x)
x = self.pool3(x)
x=self.flatten(x)
x=self.linear1(x)
x=self.linear2(x)
return x
test1=test()
#对网络结构进行检验
input=torch.ones((64,3,32,32))
output=test1(input)
print(output.shape)
output:
#torch.Size([64, 10])
用nn.Sequential将代码变得更简洁:
class test(nn.Module):
def __init__(self):
super(test, self).__init__()
self.model1=nn.Sequential(
nn.Conv2d(3, 32, 5, padding=2, stride=1),
nn.MaxPool2d(2),
nn.Conv2d(32, 32, 5, stride=1, padding=2),
nn.MaxPool2d(2),
nn.Conv2d(32, 64, 5, stride=1, padding=2),
nn.MaxPool2d(2),
nn.Flatten(),
nn.Linear(1024, 64),
nn.Linear(64, 10)
)
def forward(self,x):
x=self.model1(x)
return x
毕设
学弟初稿已交,项目正在搭建,保持联系。
总结
一是:对于Transformer类模型应用于时序任务,主要分为网络模型的修改以及应用领域两个角度:
-
网络的修改:主要围绕着位置编码、注意力机制以及模型层级设计进行展开;
-
应用领域:主要围绕着时序预测、时序分类以及异常值检测进行展开。
具体的关于Transformer类模型应用在时序预测文献可详见:Transformer应用于时序任务的综述
二是:对于空间计量分析,需要重新考量解释变量与被解释变量,如何建立合适的面板数据,合适的权重矩阵等,以及之间应该如何去建立空间计量模型,如何优化生态环境与经济环境的相关关系。
三是: 抓紧学习模型框架代码,从最基础的模型与利用现有数据集,到搭建自己的模型与利用自己的时序数据去做一些预测实现是近期的任务。