一篇博客搞定深度学习基本概念与反向传播

目录

• 深度学习的发展过程

• 深度学习的步骤

  • • 定义Neural NetWork

      • 全前向连接

      • softmax介绍

    • 定义loss函数

    • 定义优化器选择最优参数optimization

      • 反向传播Backpropagation

深度学习介绍

反向传播视频

深度学习的发展过程

• perceptron(liner model)感知机——线性模型

• perceptron is limited 线性模型是有限的，不能表示一些复杂的折线变化或者一些曲线变化

• multi layer perceotron 利用多个隐含层去贴合复杂的折现变化或者曲线

• backpropagation 反向传播，用于更新参数

• a layer can solve everthing 只用一层，这层无限宽即可解决所有问题——wide learning

• RBM initialization 用于optimization时的设置参数初始化值

• GPU加速

• 用于语音识别方面

• 用于图像处理

深度学习的步骤

同机器学习一样，仍包括 定义带有未知参数的函数（Neural Network）、定义损失函数与选择最优参数三个步骤。

定义Neural NetWork

全前向连接

下面以激活函数为sigmoid为例

$$z=W\times x+b,a=f_A(z),之后z^{\prime }=W^{\prime }\times a+b^{\prime },a^{\prime }=f_A(z^{\prime })$$

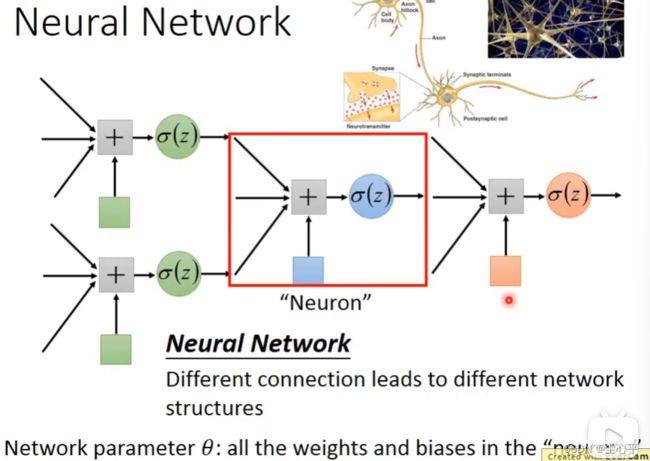
给定神经网络network structure不同的参数，会产生不同的函数（这些函数对于同一个向量的输 入会有不同的向量输出）。也就是说我们可以用network定义一个函数集

• 神经网络大致包含输入层、隐含层、输出层。其中隐含层和输出层都是由若干个神经元（利用激活函数计算一次）组成。输入层无神经元，只是输入的向量。

• 含有多个隐含层的神经网络即称之为深度学习Deep Learning

• 输出层做Multi-class Classifier进行多级分类。输出层利用前一个隐含层的输出结果，通过SoftMax函数得到最后的输出。

• 需要定义的超参数有：输入层的维度，隐含层的个数，隐含层内神经元的个数，输出层的维度，用什么样的激活函数

softmax介绍

https://zhuanlan.zhihu.com/p/105722023

softmax函数是与hardmax相对应的。我们一般找数组中最大的元素值即用到的是hardmax。hardmax最大的特点就是只选出其中一个最大的值，即非黑即白。而softmax则是对每一个结果都赋予可能的概率值(0~1)，表示属于每个类别的可能性。一般选取所有结果中概率值最大的为预测结果。其基本公式如下：

$$softmax(z_i)=\frac{e^{(}{z}_i)}{{\sum }_{j=1}^n{e}^{(}{z}_j)},z_i为第i个结点的最后一个隐含层的输出值$$

定义loss函数

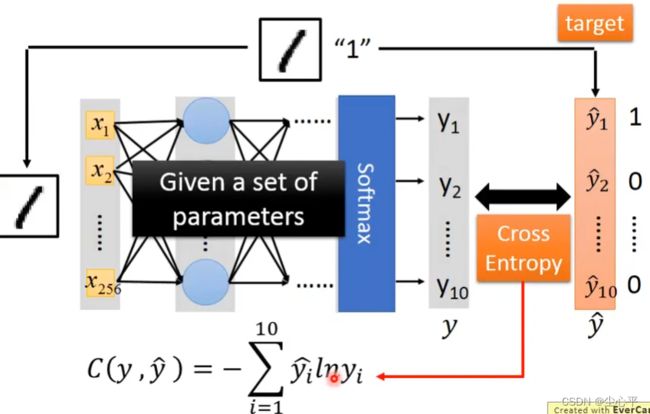
采用softmax，一般的loss函数定义为交叉熵损失函数。将某个样本对应得到的分类结果与相对应的hardmax所得到的结果作交叉熵。其中hardmax的结果为y’，softmax的结果为y，求单个样本的交叉熵公式如下：

$$C(y,y^{\prime })=-\sum _{i=1}^n(y_i^{\prime }ln{y}_i),n为共多少个类别$$

那么一次batch的loss即是

$$tota{l}_{loss}=\sum _{i=1}^n{C}_i(y,y^{\prime }),n为batch内样本数目$$

定义优化器选择最优参数optimization

仍采用gradient方法：

$${\theta }_{i+1}={\theta }_i-\eta \times \frac{\partial Loss}{\partial {\theta }_i}$$

反向传播Backpropagation

https://zhuanlan.zhihu.com/p/115571464

反向传播仍是采用Gradient Descent。它只是一种利用链式求导法则快速计算未知参数对loss偏导的方法

• 链式求导法则

  $$z=h(y),y=g(x)则\frac{dz}{dx}=\frac{dz}{dy}\times \frac{dy}{dx}$$

  $$z=k(x,y),y=h(s),x=g(s)则\frac{dz}{ds}=\frac{\partial z}{\partial x}\times \frac{dx}{ds}+\frac{\partial z}{\partial y}\times \frac{dy}{ds}$$

• 计算未知参数对loss的偏导

也就是要求每个样本的参数对该样本结果的交叉熵的偏导

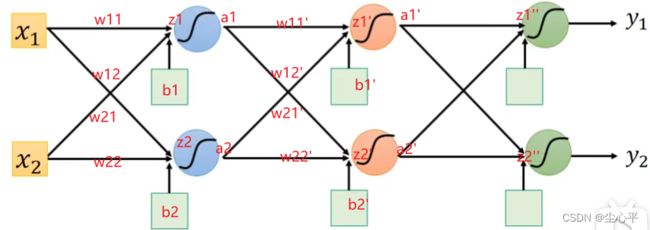
根据链式求导法则，参数w11，w21对交叉熵C的偏微分如下：

$$\frac{\partial C}{\partial w_{11}}=\frac{\partial C}{\partial z_1}\times \frac{\partial z_1}{\partial w_{11}},\frac{\partial C}{\partial w_{21}}=\frac{\partial C}{\partial z_1}\times \frac{\partial z_1}{\partial w_{21}}$$

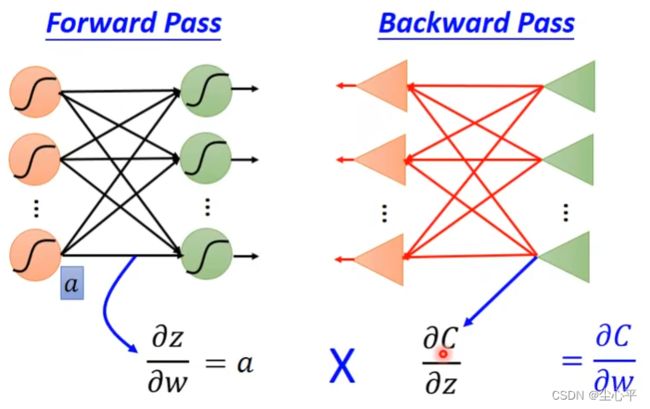
前向传播:

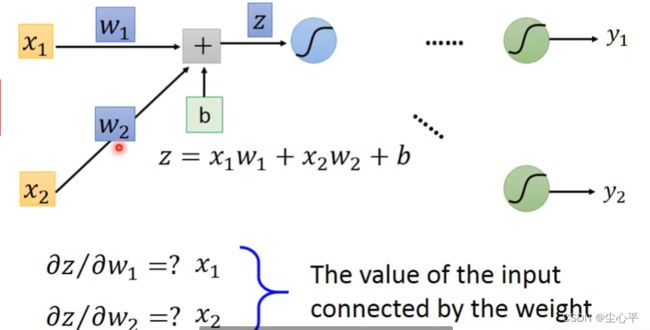
求导参数w11,w21对z的微分，这很简单，因为

$$z=x_1\times w_{11}+x_2\times w_{21}+b_1,则\frac{\partial z_1}{\partial w_{11}}=x_1,\frac{\partial z_1}{\partial w_{21}}=x_2$$

因偏导结果为参数所接的输入值，按照既定方向即可得到，故称为前向传播

反向传播

求导z1对C的偏微分，则需要再进行链式求导

$$\frac{\partial C}{\partial z_1}=\frac{\partial C}{\partial a_1}\times \frac{\partial a_1}{\partial z_1},而\frac{\partial a_1}{\partial z_1}根据确定的激活函数即可得到该值——常数$$

$$\frac{\partial C}{\partial a_1}=\frac{\partial C}{\partial z_1^{\prime }}\times \frac{\partial z_1^{\prime }}{\partial a_1}+\frac{\partial C}{\partial z_2^{\prime }}\times \frac{\partial z_2^{\prime }}{\partial a_1},z_1^{\prime }=w_{11}^{\prime }\times a_1+w_{21}^{\prime }\times a_2,\frac{\partial z_1^{\prime }}{\partial a_1}=w_{11}^{\prime }$$

$$\frac{\partial C}{\partial z_1}={\sigma }^{\prime }(z_1)\times (w_{11}^{\prime }\frac{\partial C}{\partial z_1^{\prime }}+w_{12}^{\prime }\frac{\partial C}{\partial z_2^{\prime }})$$

$$而\frac{\partial C}{\partial z_1^{\prime }}=\frac{\partial C}{\partial a_1^{\prime }}\times \frac{\partial a_1^{\prime }}{\partial z_1^{\prime }},后者即又是根据激活函数的导数求得的常数，前者又递推$$

因此为了求z1对C的偏导，可以反向传播，利用前向传播求出的每个z值，根据所选定的激活函数的导函数求出相对应的导函数值，以及最后隐含层输出的值对应的loss函数导函数的导函数值即可链式乘法算出z1对C的偏导

下面进行两种反向传播情况的介绍：

情况一：只有一层隐藏层

情况二：中间包含多个隐藏层

按照情况一的过程，多次递推，下面以中间包含两层的隐含层为例