【西瓜书】第5章神经网络---学习笔记

1.神经元模型

广泛定义：由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。
最基本的成分：神经元模型

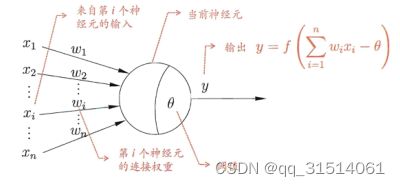
M-P神经元模型
神经元接收到来自$N$ 个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接)进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过激活函数处理以产生神经元的输出.

激活函数为模型添加非线性因素，使模型具有拟合非线性函数的能力，典型的激活函数有Sigmoid，tanh，Relu
1.Sigmoid函数：$sigmoid(x)=\frac{1}{1+e^{-x}}$

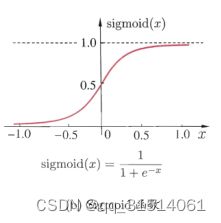
将任意输入映射到0-1之间。函数值连续，可导
缺点：
1.计算耗时，包含指数运算
2.非0均值，会导致收敛慢
3.易造成梯度消失

2.tanh函数：$tanh(x)=\frac{sinh(x)}{cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

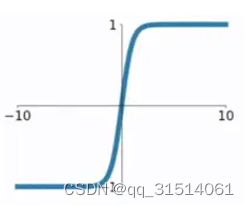
以0为均值，解决了sigmoid的一定缺点
但是依然存在梯度消失问题
计算同样非常耗时
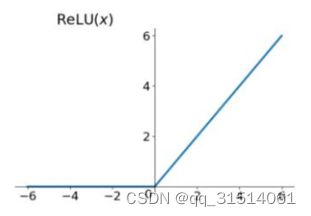
3.Relu函数：$Relu = max(0,x)$

在正区间不易发生梯度消失
计算速度非常快
一定程度上降低过拟合的风险

2.感知机与多层网络

感知机：由两层神经元组成，输入层接收外界输入信号后传递给输出层，输出层是M-P神经元

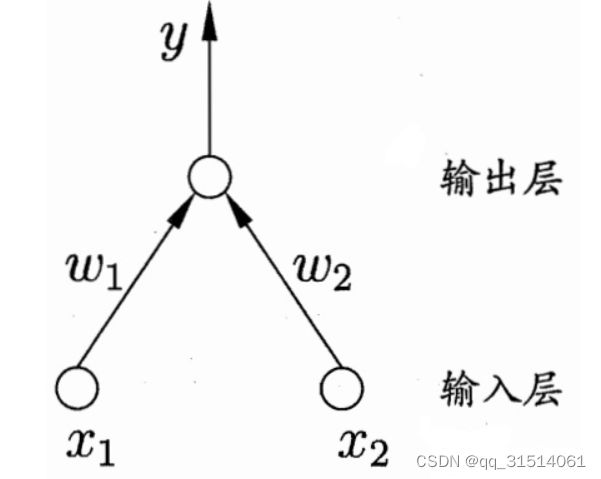
感知机能容易地实现逻辑与、或、非运算。
需注意的是，感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元，其学习能力非常有限。要解决非线性可分间题，需考虑使用多层功能神经元。

3.误差逆传播算法

BP神经网络算法它是迄今最成功的神经网络学习算法 . 现实任务中使用神经网络时， 大多是在使用BP算法进行训练 .
一个基于
手动实现梯度计算和反向传播
加入激活函数
pytorch的bp网络例子：

#coding:utf8

import torch
import torch.nn as nn
import numpy as np
import copy

class TorchModel(nn.Module):
    def __init__(self, hidden_size):
        super(TorchModel, self).__init__()
        self.layer = nn.Linear(hidden_size, hidden_size, bias=False)
        self.activation = torch.sigmoid
        self.loss = nn.functional.mse_loss  #loss采用均方差损失

    #当输入真实标签，返回loss值；无真实标签，返回预测值
    def forward(self, x, y=None):
        y_pred = self.layer(x)
        y_pred = self.activation(y_pred)
        if y is not None:
            return self.loss(y_pred, y)
        else:
            return y_pred


#自定义模型，接受一个参数矩阵作为入参
class DiyModel:
    def __init__(self, weight):
        self.weight = weight

    def forward(self, x, y=None):
        y_pred = np.dot(self.weight, x)
        y_pred = self.diy_sigmoid(y_pred)
        if y is not None:
            return self.diy_mse_loss(y_pred, y)
        else:
            return y_pred

    #sigmoid
    def diy_sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    #手动实现mse，均方差loss
    def diy_mse_loss(self, y_pred, y_true):
        return np.sum(np.square(y_pred - y_true)) / len(y_pred)

    #手动实现梯度计算
    def calculate_grad(self, y_pred, y_true, x):
        #前向过程
        # wx = np.dot(self.weight, x)
        # sigmoid_wx = self.diy_sigmoid(wx)
        # loss = self.diy_mse_loss(sigmoid_wx, y_true)
        #反向过程
        # 均方差函数 (y_pred - y_true) ^ 2 / n 的导数 = 2 * (y_pred - y_true) / n
        grad_loss_sigmoid_wx = 2/len(x) * (y_pred - y_true)
        # sigmoid函数 y = 1/(1+e^(-x)) 的导数 = y * (1 - y)
        grad_sigmoid_wx_wx = y_pred * (1 - y_pred)
        # wx对w求导 = x
        grad_wx_w = x
        #导数链式相乘
        grad = grad_loss_sigmoid_wx * grad_sigmoid_wx_wx
        grad = np.dot(grad.reshape(len(x),1), grad_wx_w.reshape(1,len(x)))
        return grad

#梯度更新
def diy_sgd(grad, weight, learning_rate):
    return weight - grad * learning_rate

#adam梯度更新
def diy_adam(grad, weight):
    #参数应当放在外面，此处为保持后方代码整洁简单实现一步
    alpha = 1e-3  #学习率
    beta1 = 0.9   #超参数
    beta2 = 0.999 #超参数
    eps = 1e-8    #超参数
    t = 0         #初始化
    mt = 0        #初始化
    vt = 0        #初始化
    #开始计算
    t = t + 1
    gt = grad
    mt = beta1 * mt + (1 - beta1) * gt
    vt = beta2 * vt + (1 - beta2) * gt ** 2
    mth = mt / (1 - beta1 ** t)
    vth = vt / (1 - beta2 ** t)
    weight = weight - (alpha / (np.sqrt(vth) + eps)) * mth
    return weight

x = np.array([1, 2, 3, 4])  #输入
y = np.array([3, 2, 4, 5])  #预期输出

#torch实验
torch_model = TorchModel(len(x))
torch_model_w = torch_model.state_dict()["layer.weight"]
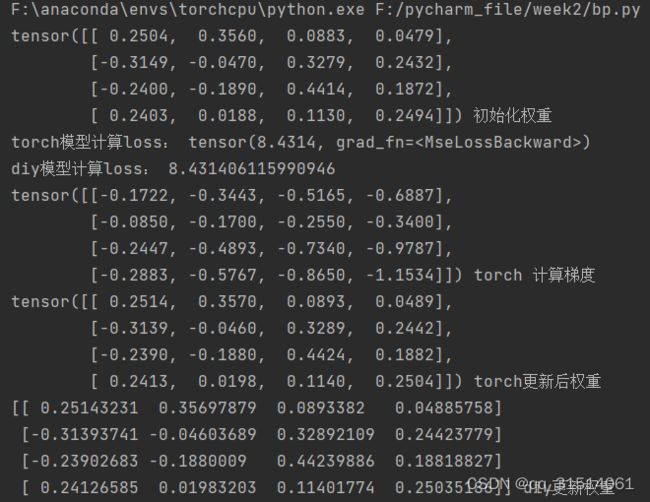
print(torch_model_w, "初始化权重")
numpy_model_w = copy.deepcopy(torch_model_w.numpy())

torch_x = torch.FloatTensor([x])
torch_y = torch.FloatTensor([y])
#torch的前向计算过程，得到loss
torch_loss = torch_model.forward(torch_x, torch_y)
print("torch模型计算loss：", torch_loss)
# #手动实现loss计算
diy_model = DiyModel(numpy_model_w)
diy_loss = diy_model.forward(x, y)
print("diy模型计算loss：", diy_loss)
#
# #设定优化器
learning_rate = 0.1
# optimizer = torch.optim.SGD(torch_model.parameters(), lr=learning_rate)
optimizer = torch.optim.Adam(torch_model.parameters())
optimizer.zero_grad()
#
# #pytorch的反向传播操作
torch_loss.backward()
print(torch_model.layer.weight.grad, "torch 计算梯度")  #查看某层权重的梯度

# #手动实现反向传播
grad = diy_model.calculate_grad(diy_model.forward(x), y, x)
# print(grad, "diy 计算梯度")
#
# #torch梯度更新
optimizer.step()
# #查看更新后权重
update_torch_model_w = torch_model.state_dict()["layer.weight"]
print(update_torch_model_w, "torch更新后权重")
#
# #手动梯度更新
# diy_update_w = diy_sgd(grad, numpy_model_w, learning_rate)
diy_update_w = diy_adam(grad, numpy_model_w)
print(diy_update_w, "diy更新权重")

4.全局最小与局部最小

全局最小(global minimum)解：参数空间中所有点的误差函数值均不小于该点的误差函数值
参数空间内梯度为零的点，只要其误差函数值小于邻点的误差函数值 ，就是局部极小点 ;可能存在多个局部极小值 ，但却只会有一个全局最小值. 也就是说 “全局最最小” 一定是局部极小，有两个局部极小但只有其中之一是全局最小 .显然，我们在参数寻优过 程中是希望找到全局最小。

5.常见神经网络

5.1RBF神经网络

RBF是一种单隐层前馈神经网络，它使用径向基函数作为隐层神经元激活函数，而输出层则是对隐层神经元输出的线性组合
$\phi (x)={\Sigma }_{i=1}^q{w}_i\rho (x_i,c_i)$
其中q为隐层神经元个数，$c_i和w_i$为中心和权重，$\rho (x_i,c_i)$是径向基函数。
训练RBF网络：
1.确定神经元中心，常用的方式包括随机采样、聚类等
2.利用 BP 算法等来确定参数连接权和阈值

5.2ART网络

竞争型学习采用无监督学习策略：
比较层：负责接收输入样本，并将其传递给识别层神经元
识别层：识别层每个神经元对应一个模式类
识别阈值：若输入向量与获胜神经元所对应的代表向量之间的相似度大于识别阈值，则当前输入样本将被归为该代表向量所属类别，同时，网络 连接权将会更新，使得以后在接收到相似输入样本时该模式类会计算出更大的相似度，从而使该获胜神经元有更大可能获胜
若相似度不大于识别阈值，则重置模块将在识别层增设一个新的神经元，其代表向量就设置为当前输入向量。

5.3SOM网络

自组织映射网络SOM：能将高维输入数据映射到低维空间，同时保持输入数据在高维空间的拓扑结构，即将高维空间中相似的样本点映射到网络输出层中的邻近神经元。
训练过程：
1.接收到一个训练样本后，每个输出层神经元会计算该样本与自身携带的权向量之间的距离，
2.距离最近的神经元成为竞争获胜者，称为最佳匹配单元
3.最佳匹配单元及其邻近神经元的权向量将被调整，以使得这些权向量与当前输入样本的距离缩小
4.这个过程不断迭代，直至收敛

5.4级联相关网络

级联相关网络是结构自适应网络的代表
级联：建立层次连接的层级结构
相关：通过最大化新神经元的输出与网络误差之间的相关性来训练相关的参数

5.5Elman网络

递归神经网络（允许网络中出现环形结构，从而可让一些神经元的输出反馈回来作为输入信号）

5.6Boltzmann机

基于能量的模型（能量最小化时网络达到理想状态）
其神经元分为两层：显层与隐层
显层：表示数据的输入与输出
隐层：数据的内在表达
Boltzmann 机中的神经元都是布尔型的，只能取0，1两种状态。

6.深度学习

基于pytorch手动实现CNN与torch做对比

#coding:utf8

import torch
import torch.nn as nn
import numpy as np


"""
使用pytorch实现CNN
手动实现CNN
对比
"""

class TorchCNN(nn.Module):
    def __init__(self, in_channel, out_channel, kernel):
        super(TorchCNN, self).__init__()
        self.layer = nn.Conv2d(in_channel, out_channel, kernel, bias=False)

    def forward(self, x):
        return self.layer(x)

#自定义CNN模型
class DiyModel:
    def __init__(self, input_height, input_width, weights, kernel_size):
        self.height = input_height
        self.width = input_width
        self.weights = weights
        self.kernel_size = kernel_size

    def forward(self, x):
        output = []
        for kernel_weight in self.weights:
            kernel_weight = kernel_weight.squeeze().numpy() #shape : 2x2
            kernel_output = np.zeros((self.height - kernel_size + 1, self.width - kernel_size + 1))
            for i in range(self.height - kernel_size + 1):
                for j in range(self.width - kernel_size + 1):
                    window = x[i:i+kernel_size, j:j+kernel_size]
                    kernel_output[i, j] = np.sum(kernel_weight * window) # np.dot(a, b) != a * b
            output.append(kernel_output)
        return np.array(output)


x = np.array([[0.1, 0.2, 0.3, 0.4],
              [-3, -4, -5, -6],
              [5.1, 6.2, 7.3, 8.4],
              [-0.7, -0.8, -0.9, -1]])  #网络输入

#torch实验
in_channel = 1
out_channel = 3
kernel_size = 2
torch_model = TorchCNN(in_channel, out_channel, kernel_size)
print(torch_model.state_dict())
torch_w = torch_model.state_dict()["layer.weight"]
# print(torch_w.numpy().shape)
torch_x = torch.FloatTensor([[x]])
output = torch_model.forward(torch_x)
output = output.detach().numpy()
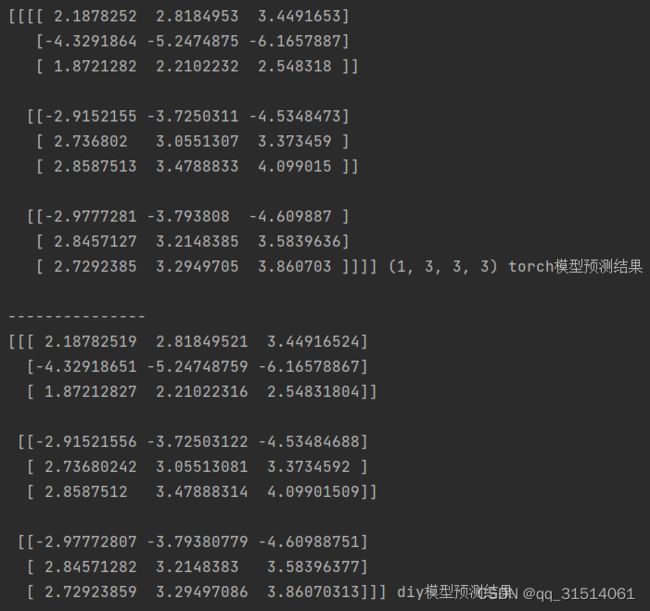
print(output, output.shape, "torch模型预测结果\n")
print("---------------")
diy_model = DiyModel(x.shape[0], x.shape[1], torch_w, kernel_size)
output = diy_model.forward(x)
print(output, "diy模型预测结果")

可以看出两个模型的输出基本一致。
DNN

#coding:utf8

import torch
import torch.nn as nn
import numpy as np


"""
手动实现简单的神经网络
用两种框架实现单层的全连接网络
不使用偏置bias
"""

class KerasModel:
    def __init__(self, input_size, hidden_size1, hidden_size2):
        self.model = Sequential()
        self.model.add(keras.layers.Dense(hidden_size1, use_bias=False))
        self.model.add(keras.layers.Dense(hidden_size2, use_bias=False))
        self.model.compile(optimizer="adam")
        self.model.build((1, input_size))

    def forward(self, x):
        return self.model.predict(x)

class TorchModel(nn.Module):
    def __init__(self, input_size, hidden_size1, hidden_size2):
        super(TorchModel, self).__init__()
        self.layer1 = nn.Linear(input_size, hidden_size1, bias=False)
        self.layer2 = nn.Linear(hidden_size1, hidden_size2, bias=False)

    def forward(self, x):
        hidden = self.layer1(x)
        # print("torch hidden", hidden)
        y_pred = self.layer2(hidden)
        return y_pred

#自定义模型
class DiyModel:
    def __init__(self, weight1, weight2):
        self.weight1 = weight1
        self.weight2 = weight2

    def forward(self, x):
        hidden = np.dot(x, self.weight1.T)
        y_pred = np.dot(hidden, self.weight2.T)
        return y_pred


x = np.array([1, 0, 0])  #网络输入

#torch实验
torch_model = TorchModel(len(x), 5, 2)
print(torch_model.state_dict())
torch_model_w1 = torch_model.state_dict()["layer1.weight"].numpy()
torch_model_w2 = torch_model.state_dict()["layer2.weight"].numpy()
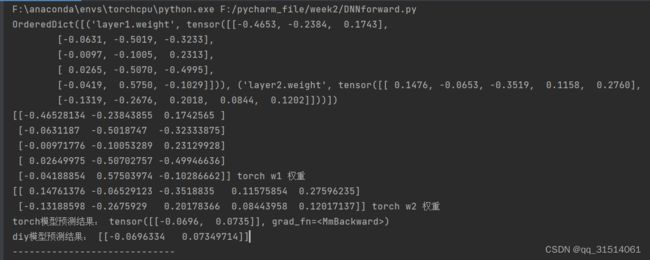
print(torch_model_w1, "torch w1 权重")
print(torch_model_w2, "torch w2 权重")
torch_x = torch.FloatTensor([x])
y_pred = torch_model.forward(torch_x)
print("torch模型预测结果：", y_pred)

diy_model = DiyModel(torch_model_w1, torch_model_w2)
y_pred_diy = diy_model.forward(np.array([x]))
print("diy模型预测结果：", y_pred_diy)
print("-----------------------------")