西瓜书第五章神经网络笔记
神经网络
根据是 T.Kohonen 1988 年在 ur Networks 创刊给出的定义,神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能模拟生物神经系统对真是世界物体所作出的交互反应。一个经典问题是神经网络与机器学习的区别在于什么?具体可参考这篇博客
下面我给出结论:
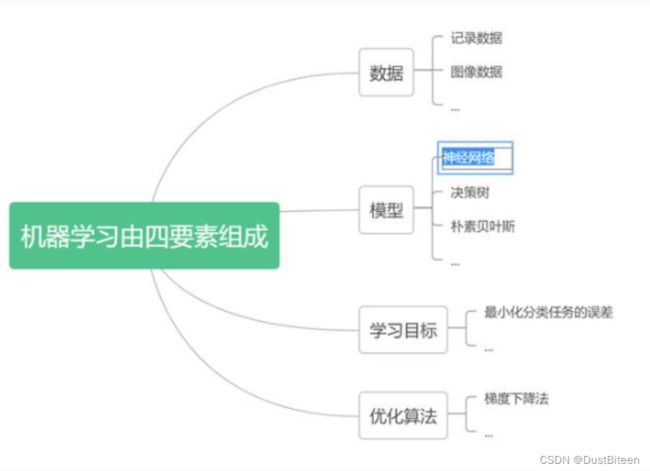
机器学习是计算机程序基于给定的有限的数据,选定某个学习目标,建立模型学习,并通过优化算法优化参数,直到满足指标要求的整个过程,最后这个模型将被用于实际的数据分析与预测。由此我们观察到机器学习有以下关键要素:
- 数据
- 模型
- 优化算法
- 学习目标
而我们说的神经网络仅是隶属于模型一类
神经元模型
生物神经网络做出反应的整个过程:当某个神经元处于兴奋状态,他会向与他相连的神经发送化学物质,改变这些神经元的电位,而当神经元的电位超过某个阈值(bias),他就会被激活并进入兴奋状态。
于这样的思想,[McCulloch and Pitts, 1943] 提出了‘M-P神经元模型’。在这个模型中,化学物质抽象成了输入信号,不同的神经连接拥有不同的权重 。整体过程是:神经元接收其他n个神经元的输入信号,这些输入信号通过带有不同权重的神经连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,并通过激活函数处理产生神经元的输出。
 在这里比较需要关注的是激活函数。我们需要回答这几个问题:1 激活函数的意义 2 激活函数的种类有哪些
在这里比较需要关注的是激活函数。我们需要回答这几个问题:1 激活函数的意义 2 激活函数的种类有哪些
对于第一个问题,我们首先设想如果没有激活函数,那么输入值的总和将直接与阈值进行比较来判断神经元是否兴奋,这其实是不合理的。这样子是默认神经元的状态与输入值呈线性关系。无论神经网络有多少层,都只是线性模型的叠加,而现实中非线性模型远多于线性模型。因此为了引入非线性因素,我们需要一个函数将输入值总和映射至一个平滑连续的非线性函数。
感知机与多层网络
感知机由两层神经元组成,如图、
:

输入层接收外界输入,第二层为M-P神经元,亦称“阈值逻辑单元”给个各神经连接的权重 w i ( i = 1 , 2 , … , n ) w_i(i=1,2,\dots,n) wi(i=1,2,…,n)以及阈值 θ \theta θ可通过训练得到。
为了统一形式, θ \theta θ视为一个权重 w n + 1 w_{n+1} wn+1,这各权重乘以固定输入-1.0。这样权重与阈值的学习统一为权重学习。
算法是怎么样的?
对训练样例 ( x , y ) (x,y) (x,y),设当前感知机输出为 y p y^{p} yp,则感知机权重这么调整
η \eta η:学习率,代表算法对每个“错误”的在意程度
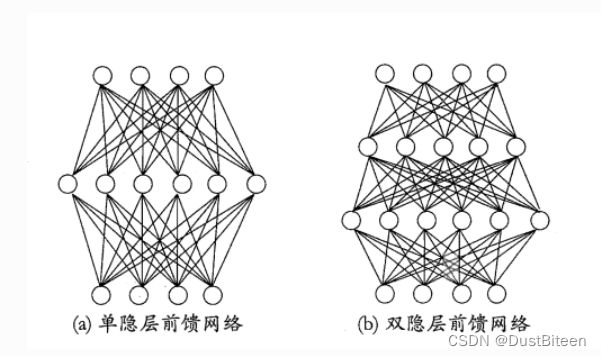
一般来说,神经网络的层数不仅只有两层,加载输入层与输出层之间的神经曾称为“隐藏层”,隐藏层与输出层都是具有激活函数的功能神经元
下面我们来探讨神经网络的一般形式
特点:
- 每一层神经单元与下一层神经单元完全互连
- 同层神经元之间不互连,也不存在跨层连接
这样的神经网络结构叫做“多层前馈神经网络”
工作流程为:
输入层神经元接收外界输入,隐藏层与输出层神经元对信号进行加工。最终在输出层神经元输出结果。
在这过程中不断调整的是神经元之间的“连接权”与每个功能神经元的阈值
误差逆传播算法(BP算法)
这节是重点,对神经网络的整个训练过程的重点就在于采用什么样的算法不断调整参数。
对于多层神经网络,公式(5.1)所采取的算法显然不再适合。误差逆传播算法(BackPropagation)算法是迄今最成功的神经网络学习算法,见名称BP算法,使用BP算法进行训练的神经网络一般叫“BP网络”
BP算法详解
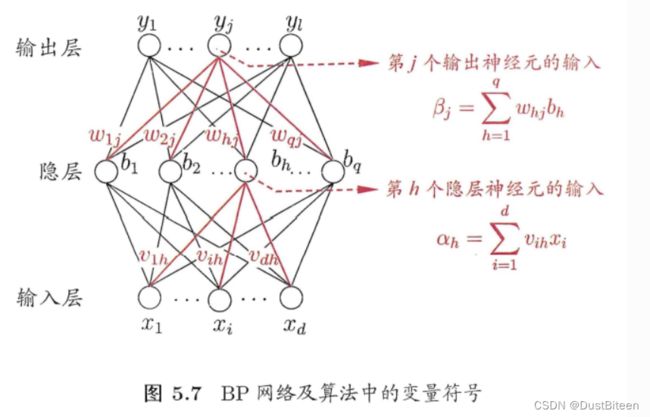
参数说明;
D:数据集,形如 ( x 1 , y 1 ) , … ( x n , y n ) {{(x_1,y_1)},\dots{(x_n,y_n)}} (x1,y1),…(xn,yn)
d ,样本的属性个数, x i ∈ R d d,样本的属性个数,x_i\in R^d d,样本的属性个数,xi∈Rd:
l ,结果的种类个数, y i ∈ R l l,结果的种类个数,y_i\in R^l l,结果的种类个数,yi∈Rl:
q : 隐藏神经元的个数 q:隐藏神经元的个数 q:隐藏神经元的个数
θ j \theta_j θj:输出层第j个神经元的阈值
γ h \gamma_h γh:隐藏层第h个神经单元的阈值
v i h v_{ih} vih:输入层第i个神经元与隐藏层第h个神经单元的来凝结权重
w h j : 隐藏层第 h 个神经元和输出层第 j 个神经元之间的连接权 w_{hj}:隐藏层第h个神经元和输出层第j个神经元之间的连接权 whj:隐藏层第h个神经元和输出层第j个神经元之间的连接权
α h = ∑ i = 1 d v i h x i \alpha_h=\sum_{i=1}^{d}v_{ih}x_{i} αh=∑i=1dvihxi 隐藏层第h个神经元接收到的输入
b h b_h bh:隐藏层第h个神经元的输出A
β j = ∑ i = 1 q w h j b h \beta_j=\sum_{i=1}^{q}w_{hj}b_{h} βj=∑i=1qwhjbh:输出层第j个神经元接收到的输入
$y^p_{k} :对于训练例 :对于训练例 :对于训练例(x_k,y_k)的输出 , 形如 ,形如 ,形如(y_1{pk},y_2{pk},y_3{pk},\dots,y_l{pk})$
y j p k = f ( β j − θ j ) (5.3) y_j^{pk}=f(\beta_j-\theta_j)\tag{5.3} yjpk=f(βj−θj)(5.3)
网络早 ( x k , y k ) (x_k,y_k) (xk,yk)上 的均方误差为
E k = 1 2 ∑ j = 1 l ( y j p k − y j k ) 2 (5.4) E_k=\frac{1}{2}\sum_{j=1}{l}(y_j^{pk}-y_j^k)^2\tag{5.4} Ek=21j=1∑l(yjpk−yjk)2(5.4)
我们需要学习的参数有
- 输入层到隐藏层的dxq个权重
- 隐藏层到输出层的qxl个权重
- 隐藏层与输出层的q+l个阈值
对于任意参数v,我们的算法为
v ← v + Δ v (5.5) v\leftarrow v+\Delta v\tag{5.5} v←v+Δv(5.5)
接下来便是BP算法的具体数学推导,由于篇幅问题在这里不做赘述
1标准BP算法与累积BP算法
在这里是针对每个训练样例的误差对参数进行调整,这样称为“标准BP算法”。如果是遍历整个数据集D一遍后再更新参数,以累积误差最小为目标,这样的算法叫做累计BP算法。它们之间的区别在于:
- 标准BP算法每次针对单个样例更新,因此一些更新的效果由于样例的影响可能被抵消掉,为了答案都同样的累计误差极小点,便准BP算法需要更多次的训练
- 但累计BP算法“后劲不足”,当累计程度到达一定程度后,累计误差的下降会变得很慢,效果不如BP算法,尤其当数据集D特别大时
2 过拟合问题
当模型对训练集训练效果特别好,对测试集效果很差时我们称之发生了“过拟合”,我们有两种策略解决过拟合问题
-
早停:将数据分成训练集和验证集,训练、集用来计算梯度、更新连接权和阔值?验证集用来估计误差,若训练集误差降低但验证集误差升高,则停止训练,同时返回具有最小验证集误差的连接权和阑值
-
第二种策略是"正则化" (regularization) [Barron, 1991; Girosi et al., 1995],其基本思想是在误差目标函数中增加一个用于描述网络复杂度的部分,例如连接权与阔值的平方和.仍令 Ek 表示第 个训练样例上的误差?叫表示连接权和阙值,则误差目标函数 改变为
全局最小与局部最小
全局最小:
参数空间中所有点的误差函数值均不小于该点的误差函数值
局部最小:
参数空间中的某个点,其邻域点的误差函数值均不小于该点的误差函数值
两者对应的 E ( w ∗ ; θ ∗ )就是对应的取值点 E(w^*;\theta^*)就是对应的取值点 E(w∗;θ∗)就是对应的取值点
基于梯度的搜索
显然,可能存在多个局部最小值,但往往只有一个全局最小值。在参数搜寻过程中,我们从某些初始解触发,每次迭代计算误差函数在当前的梯度,然后沿着负梯度方向(函数值下降最快的方向)搜寻最优解。当某一时刻当前误差函数的梯度为0,则代表着达到了局部最小,参数迭代停止。我们期望这个局部最小就是全局最小,但现实往往并非如此
对于这种不幸的情况,我们称参数陷入了局部最小。
相应的应对方法有
* 以多组不同的参数值初始化神经网络,取求得误差最小的解作为最终参数
* 使用"模拟退火"算法 ,该算法每次以一定概率接受比当前解更差的结果。
* 使用随机梯度下降,这样计算出来的梯度增加了随机因素,可能跳出局部最优解
上述方法大部分都为启发式算法,不能保证找到最优解
其他常见神经网络
在这里书上只给了简单介绍,可自行查资料进行深入的阅读
- RBF网络
- ART网络
- SOM网络
- 级联网络
- Elman网络
- Boltzmann机