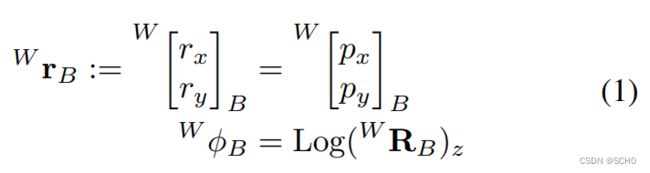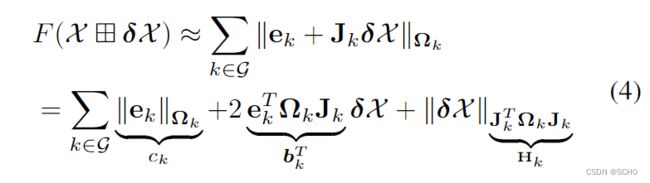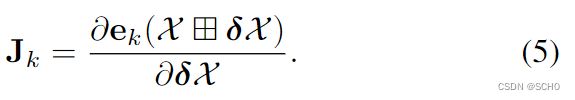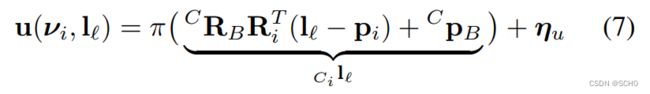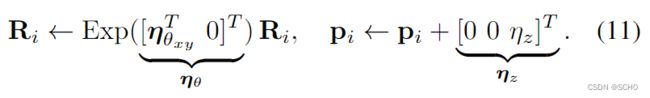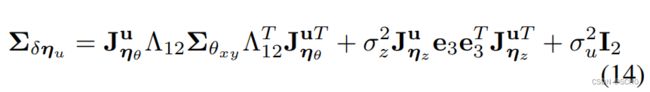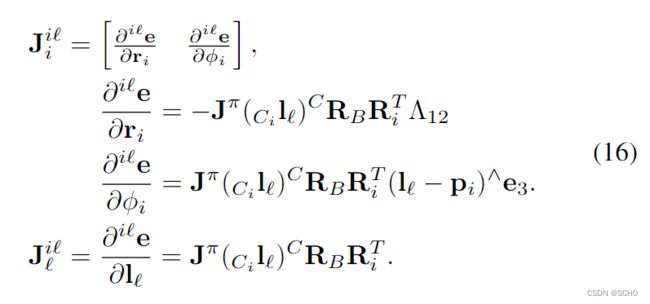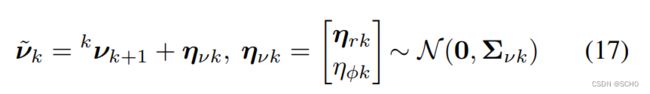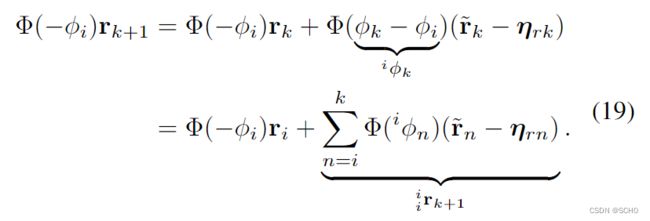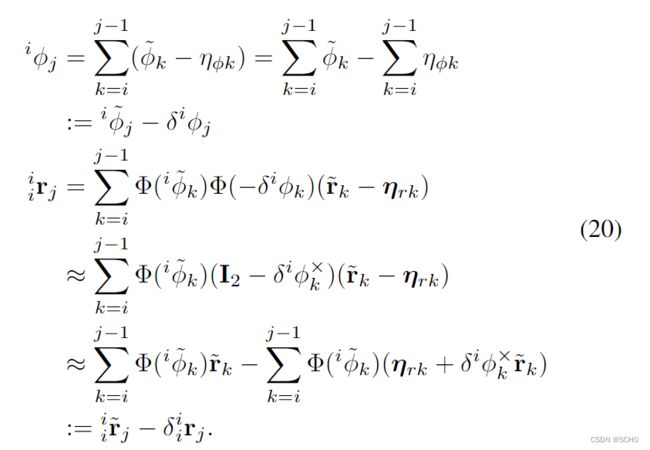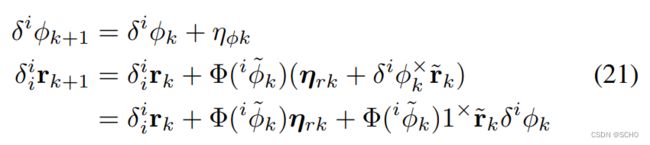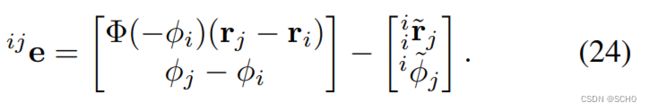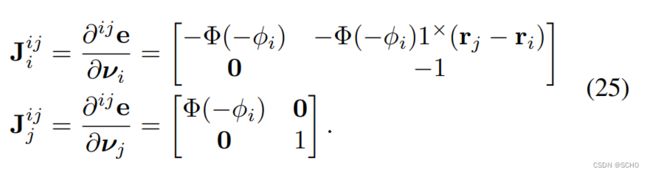se2lam翻译：基于 SE (2)-XYZ 约束的地面车辆视觉-轮速计定位与建图
摘要-本文关注的是地面车辆使用轮速计和单目视觉传感器的SLAM问题，为了改进基于视觉的地面车辆估计精度，研究人员利用了近似平面运动的约束，通常将其作为 SE (3)位姿的随机约束来实现，在本文中提出了一个更简单的算法，直接使用 SE (2)参数化地面车辆的位姿。超出 SE (2)的运动扰动并未被忽略，而是被纳入一个新的 SE (2)-XYZ 约束的综合噪声项中，该约束通过图像特征测量将 SE (2)位姿与三维地标相关联。对于里程测量的处理，我们还提出了一种有效的 SE (2)预积分算法。利用这些约束在一个图优化结构中开发了一个完整的视觉-轮速计定位和建图系统，在工业室内环境中的实际测试验证了该算法在精度和鲁棒性方面的优越性能。
一、引言
在未知环境中对移动车辆进行定位和绘制地图是自主机器人导航的基本任务。在过去20年里，在开发移动机器人定位的视觉方面已经做出了广泛的努力。然而，高精度和鲁棒的视觉定位和建图仍然具有挑战性。同时，具有特殊几何结构的机器人平台的视觉状态估计问题有待进一步研究滤波视觉。
视觉SLAM的主流方法可以分为滤波和优化两块，像 MonoSLAM [2]这样的滤波方法通过运动模型迭代地预测机器人的状态，并使用传感器测量来更新它。优化方法最小化所有来自运动和测量约束形成的代价函数，如PTAM[3]和ORB-SLAM[4][5]，依赖于图像特征和最小化重投影误差。还提出了对像素强度进行处理和最小化光度误差的直接法。
单目视觉经常和IMU或者轮速计融合实现鲁棒和真实尺度的估计，MSCKF 是一个经典的基于滤波的视觉惯性导航系统（VINS），他维持滑动窗口内几帧的位姿以提高准确性，对于基于优化的 VINS，Forster 等[8]引入了预积分理论来迭代生成两个关键帧之间的惯性约束。最先进的VINS方法包括[9][10][11]，[9]使用非线性优化进行视觉惯性估计，[10][11]添加了回环检测和地图融合，像车轮编码器这样的轮速传感器通常可以在轮式机器人中使用，并且可以在优化框架中相似的与视觉融合[12][13]。一些工程融合惯性传感器和车轮编码器与视觉[14][15]。
上述方法用于3D空间的导航，对于地面导航通常只对SE(2)位姿感兴趣，车辆平面运动（或接近平面）的约束可以用来帮助状态估计。Lategahn等[16]提出了一种基于滤波的地面车辆解决方案，其中 SE (2)姿态表示为3自由度矢量。Scaramuzza [17]进一步考虑了轮式机器人的瞬时旋转中心(ICR)约束，表明视觉估计可以用一个点来完成。确定性 SE (2)约束的主要问题是，在现实环境中，由于地形的粗糙或运动的摇晃，车辆的运动往往超出了约束模型。这可能会降低视觉估计的性能，因为所有的SE(3)的6自由度是和视觉观测到的路标点高度耦合的。在[18]中的实验表明，虽然约束模型在异常点去除后可能是良好的，但一般模型提供了更好的估计结果。
为了更有效地利用平面运动约束，随机 SE (2)-约束已经在一些最近的工作[15][13][19]中提出。随机约束通常被实现为一元约束的 SE (3)车辆姿态，允许小扰动的 SE (2)。与这些方法不同的是，本文提出的地面车辆的位姿可以直接在SE (2) 进行参数化 ，而不忽略超出 SE (2)的运动扰动。这是由于考虑到SE（2）以外的扰动通常只会显著影响视觉测量，因此，可以纳入到视觉约束。我们通过提出一个新的 SE (2)-XYZ 约束来实现这一点。
我们的贡献可以概括如下：首先，为了基于SE(2)的位姿估计，提出了一个新颖的SE(2)-XYZ约束，其中包括图像特征测量和超出 SE (2)运动扰动。第二，为轮速计测量提出了一个预积分算法，他直接基于SE(2)，不像之前基于SE(3)的方法[13]，最后，基于这些约束条件，提出了一个完整的定位与建图系统，证明了该系统在精度和鲁棒性方面的优越性能。实现开源在GitHub - izhengfan/se2lam: (ICRA 2019) Visual-Odometric On-SE(2) Localization and Mapping
接下来，2，3，4章从原理上介绍提出的系统，提出新的约束条件，并进行了系统实现。第5章展示实验分析，第六章总结。
二、预备知识
A.坐标系和符号
多坐标系定义如图2。
使用
分别表示从机体系B到世界系W的3D旋转矩阵和位置，![{ }^W \boldsymbol{\nu}_B=W\left[\mathbf{r}^{\prime} \phi\right]_B^{\prime}](http://img.e-com-net.com/image/info8/4e4e3f2bfed84450b0453f4f395ba46f.gif){kind=small}
表示对应的SE(2)位姿：
这里使用
表示一个三维向量的x,y,z分量，
是旋转向量和旋转矩阵的对应关系， 相反有
[8][20]，由于坐标系B相对于世界系W的状态是主要关心的，在下面简单的写为
。（二维只能绕z轴旋转，因此这里只取旋转向量的z分量）
路标点的位置被表示为l，转换到相机系C后写为cl，
。
B.非线性图优化
图优化[21]将状态估计问题表示为一个图 
，通过最小化类似下面这个代价函数寻找状态值来进行求解，
其中
中的状态参数块
表示为节点或顶点，状态的每个约束是一条边，误差函数是
，信息矩阵
作为
的加权因子，通常取决于约束的协方差矩阵的逆。
通过线性化广义增量模型（表示为田），代价函数可以被近似为：
ek的约束雅可比矩阵
将所有约束的信息矩阵、雅可比矩阵和误差放在一起
，可以构造一个高斯牛顿系统来解决增量状态
：
可以迭代的更新状态直到收敛。（这些就是解释了非线性优化过程）
3.基于SE (2)-XYZ 约束的图优化
提出的图系统包括关键帧和路标点组成的节点，从连续的帧中选出关键帧，丢弃其他帧以确保实时效率。
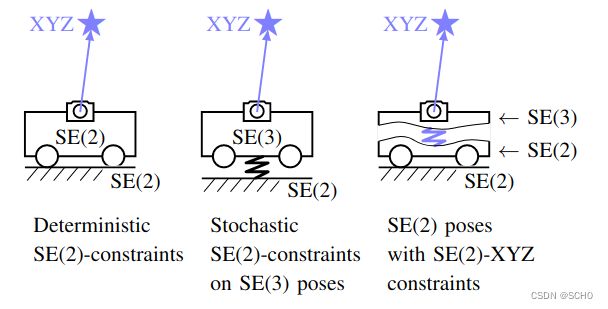
关键帧位姿直接在 SE (2)上参数化。在现实环境中，车辆可能会遇到崎岖的地形、负载变化和运动中的摇晃。这些超出SE(2)的扰动被表述为视觉测量约束，称为SE (2)-XYZ 约束，如图1所示。轮速计测量使用 SE (2)上的预积分技术进行处理。图3显示了图中提出的约束条件。
图1.SE (2)-XYZ 约束与以前模型比较的说明。确定性 SE (2)-约束在粗糙地形或地面车辆运动时不精确; 随机 SE (2)-约束在 SE (3)姿态上足够精确，但是是冗余的; SE (2)-XYZ 约束有助于保留 SE (2)姿态和非 SE (2)扰动信息。
A.基于特征的 SE (2）- XYZ 约束
基于特征的重投影误差是常见的视觉SLAM 方法中较为标准的术语。不像常规的SE3-XYZ约束，这里的关键帧使用SE2位姿参数化，提出了一种新的 SE (2)-XYZ 约束。为了防止确定性平面运动约束可能导致的精度下降，超出se2的运动不确定性也封装在 SE (2)-XYZ 约束中，并结合图像特征测量噪声来表达约束协方差。
考虑被关键帧i观察到的路标点l，给定事先标定
[22]，相关图像特征坐标的测量模型是：
是特征测量噪声，(Ri，pi)可以从 SE (2)变量中提取出来：
（二维的旋转只绕z轴，平移只有xy,这里都用三维向量表示） 
代表相机的投影方程：
其中(fx，fy)是相机的焦距，(cx，cy)是主点。很容易知道投影雅可比矩阵是：
然后把超出se2的扰动作为噪声加入公式7，假设垂直平移扰动服从
，旋转扰动是
，位姿扰动如：
测量模型(7)变成：
其中我们使用一阶近似来线性化噪声项，u关于
的雅可比计算如下：
∧表示一个反对称映射。
制定一个合成的零均值噪声
，可以近似它的协方差
由于ηθ,ηz,ηu是相互独立的，这里ei可以表示I3中的第i列![\Lambda_{12}=\left[\begin{array}{ll} \mathbf{e}_1 & \mathbf{e}_2 \end{array}\right]](http://img.e-com-net.com/image/info8/af263b0e809e4bee85831ee79c77149b.gif){kind=small}
。
我们现在可以构造 SE (2)-XYZ 约束的重投影剩余误差项，给的检测到的特征坐标
，
它的信息矩阵是 
，误差关于位姿和特征点的雅可比为
注意
代表省略
中的
，因此它可以与一起计算，而且由于计算
所带来的额外计算代价是有限的。
B.预积分轮速计约束
类似于 [8]的IMU 预积分，我们使用预积分技术在这里推导一个里程约束。类似的轮速计预积分也在[13]中提出。虽然[13]在 SE (3)上执行预积分，但我们在 SE (2)上公式化它，从而导致一个更简洁的算法。
为了达到一个更一般的公式，没有指定任何特定类型的里程传感器或任何运动学模型，我们假设里程测量提供了在两个连续的帧k 和 k+1之间的离散的时间测量：
其中
是k+1 到k时刻真实的se2位姿，带有波浪线的代表测量值，在se2上的状态传播类似于
注意，传播的
依赖于旋转状态
。 为了在不依赖于
的情况下生成两个关键帧 i 和 j 之间的测量值，我们可以在 左边乘上
，
然后，我们表示关键帧 i 和 j 之间的预积分测量和相应的噪声为：
为了预积分噪声项
的传播，考虑他们的迭代传播形式：
将（21）写出一个紧凑的形式：
因此，给定每个步长的里程测量噪声协方差
，
的协方差被传播为：
从初始条件
开始，可以与预积分测量项
一起递增地计算。
我们现在可以根据预积分的里程测量构造一个优化的误差项。给定两个带有 和
SE2位姿的关键帧，残差定义为：
根据(19)-(23)的推导，
的协方差矩阵应该是
， 关于
的雅可比分析计算为：
4.跟踪、建图和回环
受到 PTAM [3]和 ORB-SLAM [5]的启发，该系统在三个并行线程中进行估计: 跟踪、局部映射和闭环。
跟踪线程执行 III-B 中描述的里程计预积分，并使用轮速计测量初始猜测一个新帧的位姿，从帧中提取 ORB 特征[23] ，与最新关键帧中的特征相匹配，并进一步与局部地图中的地标相匹配，以获得更多的对应关系。当当前帧和最新关键帧之间有足够大的视差或时间差时，选择当前帧作为新的关键帧并插入到地图中。
局部建图管理一个局部地图
，一组后M个关键帧的集合
和他们观测到的路标点
，插入新的关键帧后，使用基于特征的 SE (2)-XYZ 约束和里程约束对地图进行优化。为了保持恒定时间的局部优化，这里最古老的关键帧被边缘化出 L地图并作为优化的先验。关键帧不在地图中，但其观测到的路标点在地图中，因此作为先验贡献于优化，则个策略的灵感来自于[10].
回环检测线程在所有关键帧之间搜索外观与当前关键帧相同场景的关键帧，基于可视化 Bags of Words [24]。如果检测到回环，两个匹配的关键帧之间的约束是基于它们的共可见路标点[19]生成的。这个约束是SE3的，根据公式1可以映射到SE2，在此之后，我们可以构造一个闭环约束，在数值上与 III-B 中的相同。利用闭环约束和里程约束对全局姿态图进行了优化。然后关于优化的关键帧调整路标点。
5.实验结论
A.实验设置
我们使用类似于[19]的实验装置。如图4-(a)所示的叉车 AGV 装有两个用于里程测量的编码器。一种编码器是 SICK DSK40增量式编码器，驱动轮上每圈分辨率为1000线程，另一种是 SICK ATM60绝对式编码器，每圈分辨率为2048线程，用于测量转向角度。在[19]中的光纤陀螺仪在这里没有使用。一个带有鱼眼镜头的 PointGrey Chameleon 2.0相机安装在车顶上，向上看，以30Hz 的频率收集640 × 480的图像。里程计和视觉传感器之间的校准和同步是离线进行的[22]。该系统使用英特尔 i7-6500U CPU 实时运行。为了收集实验数据，AGV 在两个工业室内场景中手动驱动，一个约8 × 20m2 × 3m 的小测试室名为 Dataset Room，一个约40 × 70m2 × 6m 的仓库名为 Dataset Warehouse (见图4-(b))。通过使用安装在车辆底部的二级向下观察摄像机来近似地面真实轨迹，以检测在地面上具有预先测量位置的一些标记[19]。
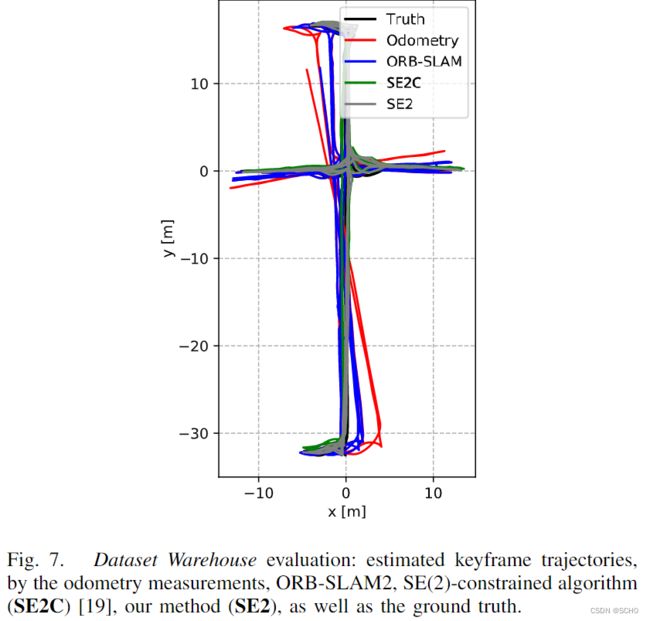
我们将我们的工作(在这里称为 SE2)与1)在[19]中的 SE (2)约束系统(称为 SE2C)和2)在两个数据集上的最先进的视觉评估系统 ORB-SLAM2[5]的里程计辅助版本。里程测量有助于 ORB-SLAM2的初始化和“运动模型跟踪”步骤。
B.结果和讨论
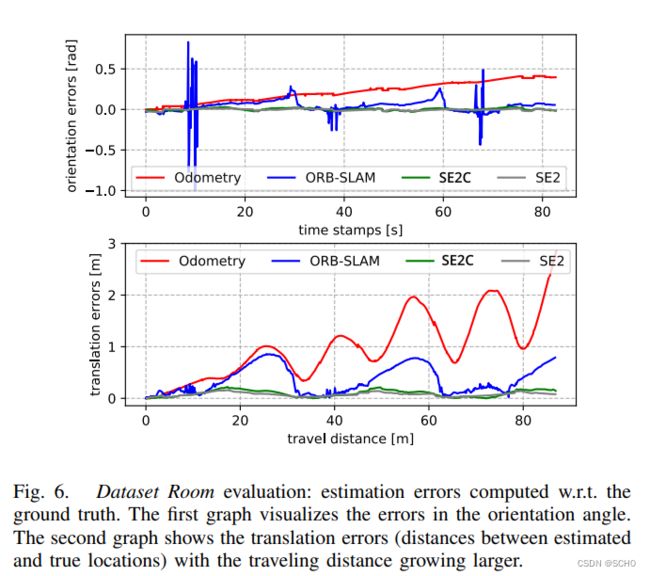
图5显示了由我们的系统 SE2估计的 Dataset Room 的轨迹，与传播的里程计，里程计辅助的 ORB-SLAM2，SE (2)约束的系统 SE2C 和地面真相相比较。
从图中可以看出，里程计辅助可视化 SLAM (ORB-SLAM2)提供的估计结果比 SE (2)约束系统和我们的 on-SE (2)方法都不准确。这说明了在车辆在平面上运动时，将平面运动约束引入状态估计问题的重要性。这种重要性也可以通过观察图9所示的估计 z 坐标来推断。ORB-SLAM2在 Dataset Room 上给出偏差和不稳定的 z 值; 类似的结果也可以在 Dataset Warehouse 上看到。由于 SE (3)姿态的所有6个自由度在涉及视觉测量时都是高度耦合的，不准确的 z 值自然会降低其他自由度的估计精度。
我们进一步研究了我们的系统相对于 SE2C 的改进。表1展示了两个数据集误差的的数值结果，我们在这里使用误差的均方根(RMSE) ，包括在 x，y，φ (偏航)坐标系下的误差，以及平移误差。在 RMSE 方面，我们的 SE2在数据仓库中的收益准确率分别为0.288% (0.085 m/29.5 m)和0.223% (0.328 m/147 m) ，均优于 SE2C (0.381% 和0.339%)。
与 SE2C 相比，我们系统的一个更重要的改进是鲁棒性。在 SE2C 的实验中，我们发现该估计对于随机 SE (2)-约束的参数设置非常敏感。有时需要相当多的手动参数调整，以使评估系统正常工作，这在实践中是不可取的。如图10中的例子所示，即使一些看起来正常的参数设置也可能导致估计的关键帧偏离地面。这可能是由于复杂系统的数值优化固有的不稳定性。我们的系统从来没有遭受这样的估计失败，由于优化图是直接在 SE (2)上公式化，导致了一个更简单的线性系统来解决。
6.结论
本文提出了一个基于里程和单目视觉传感器的地面车辆定位与建图框架。与一般SE (3)姿态参数化车辆状态视觉 SLAM 系统相比，或在SE3位姿随机应用SE2的近期作品相比。我们直接描述车辆在 SE (2)上的姿态，而不忽略现实环境中的 SE (2)外扰动，从而得到一个简单而鲁棒的估计算法。这是通过使用一种新的 SE (2)-XYZ 约束来实现的，它不仅涉及来自基于视觉特征的测量的信息，而且还将 SE (2)外的扰动合并到其集成噪声项中。我们将这些约束实施到多线程软件系统中，该系统可实时运行，以同时估计车辆位姿和地标点。与最先进的视觉SLAM系统相比，室内工业环境中的实验验证了我们系统的出色表现，以及最近提出的SE（2）估计系统，以精度和鲁棒性。
将来，将对公开可用的数据集进行更多测试，以验证拟议系统的性能。此外，在与不同传感器的更多估计问题中使用SE（2） - XYZ约束铺平了道路。我们考虑通过组合SE（2）-XYZ约束和IMU预积分技术来为地面车辆构建VINS。地面车辆的单目或双目声视觉SLAM也是一个很好的方向。