k-均值聚类算法总结

相关定义

聚类是一种无监督的学习，它将相似的对象归到同一个簇中。聚类方法几乎可以应用到所有的对象，簇内的对象越相似，聚类的效果越好。
K-均值（K-means）聚类是指将数据划分成k个不同的簇，且每个簇的中心采用簇中所含数据的均值计算而成。
聚类和分类最大不同在于，分类的目标事物已知，而聚类不一样。因为其产生的结果与分类相同，而只是类别没有预先定义，聚类有时候也被称为无监督分类。

K-均值聚类算法

K-均值是发现给定数据集的k个簇的算法。簇的个数k是用户给定的，每个簇通过其质心，即簇中所有点的中心来描述。
算法的工作流程如下：首先，随机确定k个初始点作为质心。然后将数据集中的每个点分配到一个簇中。这一步完成后，每个簇的质心更新为该簇所有点的平均值。流程的伪代码如下：

创建k个点作为初试质心
当任意一点的簇分配结果发生改变时：
	对数据集中的每个数据点：
		对每个质心：
			计算数据点与质心直接的距离
		将该数据点分配到距离最近的簇
	对每一个簇：
		更新质心坐标

该段代码涉及到的辅助函数如下：

def create_data(fname):     #导入数据
    datam=[]
    f=open(fname)
    for line in f.readlines():
        curline=line.strip().split('\t')
        floatarr=list(map(float,curline))
        datam.append(floatarr)
    return datam

def distEclud(va,vb):   #计算两点之间的距离
    return np.sqrt(np.power(va-vb,2).sum())

def randCen(datas,k):   #创建k个随机点当作质点
    n=datas.shape[1]    #获取数据特征数
    centP=np.mat(np.zeros((k,n)))   #创建k*n的质点矩阵
    for i in range(n):  #对于数据每一个特征值
        minp=min(datas[:,i])
        rangep=float(max(datas[:,i])-minp)
        centP[:,i]=minp+rangep*np.random.rand(k,1)      #通过k*1的随机向量来生成k个介于该特征值最大最小值之间的随机数
    return centP

辅助函数创建完毕后就可以写完整的k-means函数了。该算法会创建k个质心，然后将每个点分配到最近的质心，再重新计算质心。整个过程重复数次，直到数据点的簇分配结果不再发生改变为止，具体代码如下：

def k_means(dataset,k,disfun=distEclud,createP=randCen):    #普通k均值聚类
    m=dataset.shape[0]          #获取数据集的个数
    clusterAssment=np.mat(np.zeros((m,2)))  #创建矩阵，该矩阵共两列，第一列是每个数据点对应的簇的索引值，第二列是距离簇的距离
    centroids=createP(dataset,k)    #初始质心
    clusterChanged=True     #判断簇的分配是否变化
    cnt=0
    while clusterChanged:   #当分配发生变化时循环
        cnt+=1
        print(cnt)
        clusterChanged=False    #先置为false
        for i in range(m):      #对于每个数据
            minDist=np.inf      #初始化最小距离
            minIndex=-1         #初始化索引值
            for j in range(k):  #对于k个质心
                distJ=disfun(centroids[j,:],dataset[i,:])   #计算第i个数据到第j个质心之间的距离
                if distJ<minDist:       #如果当前值小于最小值，更新相关变量
                    minDist=distJ
                    minIndex=j
            #当前已经找到距离当前数据点数据最近的质点
            if clusterAssment[i,0]!=minIndex:   #如果索引值发生了改变
                clusterChanged=True
            clusterAssment[i,:]=minIndex,minDist**2 #存储当前数据点对应的簇的相关信息
        print(centroids)
        #所有数据都执行完毕后，要更新质心坐标
        for cent in range(k):   #对于k个质心
            ptsInclust=dataset[np.nonzero(clusterAssment[:,0].A==cent)[0]]      #获取全部数据集中对应当前质心的子集
            centroids[cent,:]=np.mean(ptsInclust,axis=0)        #取该簇族中所有数据的平均值来充当新的质心
    return centroids,clusterAssment

下面引入一组数据，分布如下：

可以看出该数据集大体分为4类，在执行k-means聚类代码后得到的结果如下：

1
[[ 4.47211349  2.54595758]
 [ 4.16590074  0.07622815]
 [ 1.73687885  2.83815469]
 [-0.48675348 -0.0258452 ]]
2
[[ 3.718828    3.72065725]
 [ 3.31153765 -2.50129665]
 [ 1.62862683  3.18453722]
 [-2.6530681  -0.6180039 ]]
...
6
[[ 2.6265299   3.10868015]
 [ 2.65077367 -2.79019029]
 [-2.46154315  2.78737555]
 [-3.53973889 -2.89384326]]

可以看出程序经过6次循环后收敛，得到了4个质心坐标，他们的分布如下：

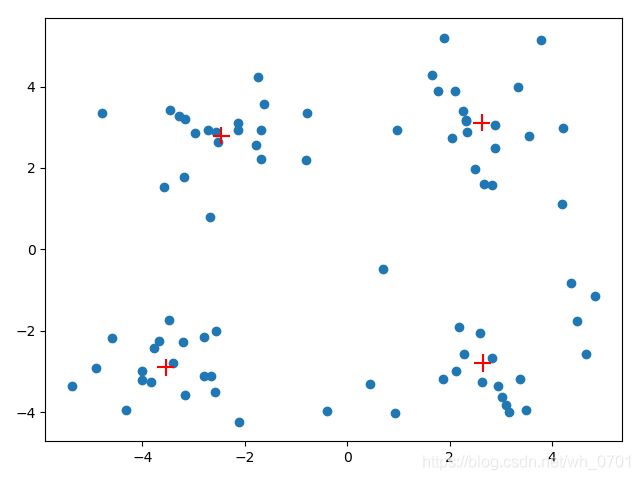
可以看出整体聚类效果较好，但这种算法仍存在一些问题。

算法不足与改进

由于k-means聚类一开始的质心选择是随机的，所以可能会出现一些问题，如下面的聚类结果：

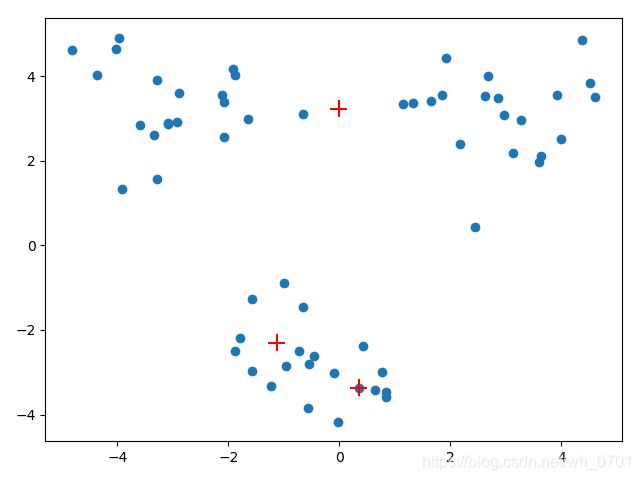
K-均值算法收敛但聚类效果差的原因是，该算法仅收敛到局部最小值，并非全局最小值（局部最小值结果还可以但不是最好结果，全局最小值是可能的最好结果）。
一种度量聚类效果好坏的指标是SSE（误差平方和），它对应的是上面算法中的clusterAssment矩阵中的第二列的平方和。SSE值越小表示数据点越接近它们的质心，聚类效果也越好。因为取了距离的平方，所以更加重视那些远离质心的点。一种可能可以降低SSE的方法就是增加簇的个数，但显然是违背目标的，聚类的目标就是不改变簇数目的前提下提高簇的质量。
另一种办法就是将具有最大SSE值的簇划分成两个簇。可以将最大簇包含的点过滤出来并在这些点上运行K-均值聚类，此时的k为2。
为了保证簇总数不变，可以将某两个簇进行合并。有两种量化方法：合并最近的质心，或者合并两个使得SSE增幅最小的质心。第一种通过计算所有质心之间的距离，然后合并距离最近的两个点。第二种方法需要合并两个簇然后计算中SSE值。必须在所有可能的两个簇上重复上述处理过程，直到找到合并最佳的两个簇为止。接下来将改进上面的方法。

二分K-均值算法

为了克服K-均值算法的收敛到局部最小值的问题，采用二分K-均值算法。首先将所有点作为一个簇，然后将簇一分为二。之后选择其中一个簇继续进行划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度的降低SSE的值。不断重复上面的划分过程，直到划分数目达到用户指定的簇数目为止。
该过程的伪代码如下：

将所有点看成一个簇
当簇数目小于k时：
	对于每一个簇：
		计算总误差
		在给定的簇上面进行K-均值聚类（k=2）
		计算将该簇一分为二后的总误差
	选择使得误差最小的那个簇进行划分操作

下面是具体的实现代码：

def biKmeans(dataset,k,distmeas=distEclud):     #二分K-均值算法
    m=dataset.shape[0]          #获取数据集行数
    clusterAssment=np.mat(np.zeros((m,2)))      #与上面的clusterAssment矩阵效果一样
    centP0=np.mean(dataset,axis=0).tolist()[0]  #将当前数据集所有点看成一个簇，计算质心坐标
    centlist=[centP0]       #将质心坐标加入到队列中
    for j in range(m):      #对于每一个数据点
        clusterAssment[j:1]=distmeas(np.mat(centP0),dataset[j,:])**2    #更新数据点到质心距离
    while (len(centlist))<k:        #当没有达到用户给定的簇数目时循环
        lowestSSE=np.inf            #初始化最小SSE
        for i in range(len(centlist)):  #对于每一个质心
            ptsInCurrCluster=dataset[np.nonzero(clusterAssment[:,0].A==i)[0],:]     #获取当前簇的所有数据构成的子集
            centroidMat,splitClustAss=k_means(ptsInCurrCluster,2,distmeas)          #对该子集进行划分
            sseSplit=sum(splitClustAss[:,1])    #划分后的新的两部分SSE值之和
            sseNoSplit=sum(clusterAssment[np.nonzero(clusterAssment[:,0].A!=i)[0],1])   #没有参加划分的数据点SSE总和
            if (sseNoSplit+sseSplit)<lowestSSE:     #如果两部分SSE相加小于当前最小值，更新相关变量
                bestCentToSplit=i
                bestNewP=centroidMat
                bestClustAss=splitClustAss.copy()
                lowestSSE=sseNoSplit+sseSplit
        #到此已经找到要划分的簇，下面进行更新簇的分配
        bestClustAss[np.nonzero(bestClustAss[:,0].A==1)[0],0]=len(centlist)
        bestClustAss[np.nonzero(bestClustAss[:, 0].A == 0)[0], 0] = bestCentToSplit
        #更新簇分配结束
        
        # 下面更新质心队列
        centlist[bestCentToSplit]=bestNewP[0,:].tolist()[0]
        centlist.append(bestNewP[1,:].tolist()[0])
        #队列更新结束
        
        # 下面更新矩阵
        clusterAssment[np.nonzero(clusterAssment[:,0]==bestCentToSplit)[0],:]=bestClustAss
        #矩阵更新结束
    return np.mat(centlist),clusterAssment

在更新簇分配的过程中，由于上面已经将要划分的簇一分为二，这时的bestClustAss矩阵中第一列只有01这两个索引。现在要更新到全局变量中，需要将01值替换，我们假定将1的索引值当做新的一个质心坐标加入进去（因为队列索引从0到n-1，新加入的索引值就是n，即数组长度），将0的索引值替换掉原来的索引值（原来的索引值就是划分前这个簇的质心索引值）。
在更新质心队列过程中。根据上面簇分配的结果，要划分的簇的质心坐标被划分后索引值为0的质心坐标替换。划分后质心坐标的索引值为1的当作新的执行坐标添加到队列中。因此按上面代码进行更新。
最后更新矩阵，因为已经没有了bestCentToSplit对应的相关数据，直接将质心索引为它的数据子集替换成上面更新好的bestClustAss矩阵。

至此新的二分K-均值算法已经完成，现在再用上面没有得到较好聚类效果的数据来做示范，发现聚类效果得到显著提升。

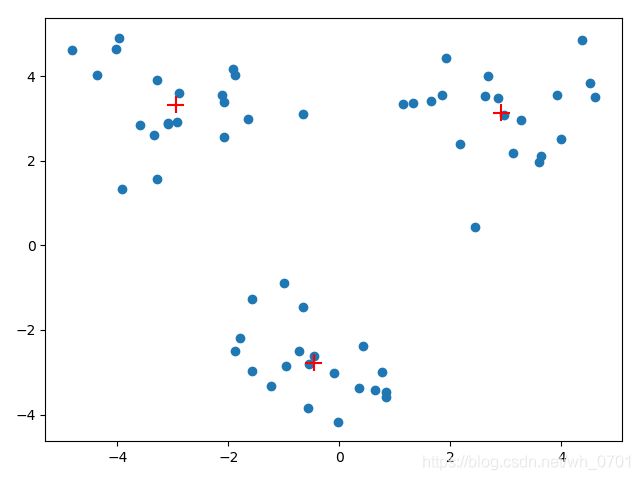
它具体的工作流程如下：