Matlab 模糊C均值聚类分析与因子分析实验报告

Matlab 模糊C均值聚类分析与因子分析实验报告

提示：数据资源在本CSDN号的上传资料中直接领取

---

1 引言

数据：gyzb.mat（按顺序对应每一列）为：31个省市区的国有控股企业的主要指标（包括：总利润（亿元）、总资产贡献率（%）、资产负债率（%）、流动资产周转次数（次/年）、工业成本费用利用率（%）和人均主营收入（万元/人））。需要使用数据分析方法对该数据进行分析，试着得到一些结论。这里使用的分析方法为：模糊C均值聚类分析、因子分析。

---

2 算法原理

2.1 模糊C均值聚类分析的简介及算法原理：

（1）简介：

模糊C均值聚类分析（FCM，Fuzzy c-means）是从C从均值算法（Hard c-means）发展而来的。模糊聚类分析是根据研究对象本身的属性来构造模糊矩阵，并在此基础上根据隶属度来确定聚类关系，即确定样本之间的模糊关系定量。

（2）算法原理：

（3）算法步骤：

【1】设置好聚类类别数，设定迭代收敛条件，初始化各个聚类中心；

【2】用当前的聚类中心，计算隶属度值度函数。

【3】使用隶属度函数，重新计算计算各个聚类的中心。

【4】重复【2】、【3】的运算，直到各个样本的隶属度稳定；

【5】当算法收敛时，就得到了各类的聚类中心和各样本对于各类的隶属度值，从而完成了模糊聚类划分。

2.2 因子分析的简介及算法原理：

（1）简介：

因子分析(factor analysis)是通过研究多个变量间相关矩阵（或协方差矩阵）的内部依赖关系，找出能综合所有变量主要信息的少数几个随机变量的一种统计分析方法、预处理方法、降维技术。这几个随机变量不能直接测量，通常称为因子。各个因子间互不相关，所有变量都可以表示成公因子的线性组合。因子分析的目的就是减少变量的数目，用少量因子（若干更基本的有代表的变量）代替所有变量去分析整个问题；这些更基本的变量也叫做公共因子或共性因子。

（2）算法原理：

设有n个样本，p个指标，X = (X1, X2, X3, ……，XP)T为随机向量，要寻找的公因子为F = (F1,F2,……，Fm)T，则模型

X1 = a11F1 + a12F2 + …… + a1mFm + ε1

X2 = a21F1 + a22F2 + …… + a2mFm + ε2

……

XP = aP1F1 + aP2F2 + …… + apmFm +εp

被称为因子模型。矩阵A = (aij)称为因子载荷矩阵，aij为因子载荷（loading）,其实质就是公因子Fi和变量Xj的相关系数。ε为特殊因子，代表公因子以外的影响因素所导致的（不能被公因子所解释的）变量变异，在实际分析时忽略不计。

对于求得的公因子，需要观察它们在哪些变量上有较大的载荷，再据此说明该公因子的实际含义。但对于分析得到的初始因子模型，其因子载荷矩阵往往比较复杂，难于对因子Fi给出一个合理解释，此时可以进一步做因子旋转，以便旋转后得到更加合理的解释。

（3）算法步骤：

【1】将原始数据标准化，以消除变量间在数量级和量纲上的不同。

【2】求标准化后的样本数据的相关系数矩阵。

【2】求其特征值和特征向量。

【3】计算方差贡献率和累积方差贡献率。

【4】确定因子。

【5】进行因子旋转，使因子变量更具有可解释性。

【6】计算因子得分。

（4）适用范围：

用途范围广泛。但要求样本数据的各个变量应当具有相关性，不彼此独立。因子分析中公因子应当具有实际意义。

---

3 实验结果与分析

(实验思路,步骤及结果分析)

3.1 模糊C均值聚类分析的实验结果与分析：

（1）实验思路：

数据文件gyzb.mat是一个每一列都是数据值的样本数据矩阵，没有可供判断类别列也没有时间值等。想到刚大致学了模糊C均值聚类分析，便考虑到选择对gyzb.mat数据文件进行模糊C均值聚类分析。 加上Matlab有强大的fcm()等自带函数，就开始实验了。

（2）实验步骤：

【1】先导入gyzb.mat数据文件，然后观察数据的大致情况；

【2】选择模糊C均值聚类分析；

【3】先在matlab脚本中写好大致的代码思路；

【4】再试着进行编写matlab代码；

【5】对运行得出的结果及统计图进行分析。

（3）结果及分析：

（3.1）matlab代码：

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * 
clc
% （1）导入样本数据
load('gyzb_data.mat');
disp('【1】模糊C均值聚类分析:')
% （2）设置类的数量为3
num_cluster = 3;
% （3）进行模糊C均值聚类分析
% num_cluster为类的数量；gyzb_data为样本数据；center是一个表示聚类中心的坐标矩阵；
% u是类组成函数矩阵，包括每类中包含的样本数据的等级，0表示空类，1表示满员，介于0~1表示部分填充的类。在每次循环中，目标函数被最小化以搜索类别的最佳位置。
% obj_fcn是最佳位置的值；
disp('(1)Iteration count为迭代次数，obj. fcn为最佳位置的值：')
[center, u, obj_fcn] = fcm(gyzb_data, num_cluster);
disp('(2)聚类中心的坐标矩阵：')
disp(center)
disp('(3)类组成函数矩阵：')
disp(u)
% （4）查找并输出隶属矩阵u每列最大值的行标，确定每个样本的类
id1 = find(u(1, :) == max(u));
id2 = find(u(2, :) == max(u));
id3 = find(u(3, :) == max(u));
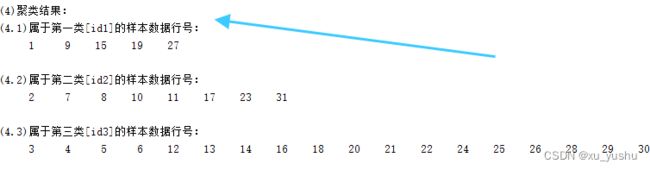
disp('(4)聚类结果：')
disp('(4.1)属于第一类[id1]的样本数据行号：')
disp(id1)
disp('(4.2)属于第二类[id2]的样本数据行号：')
disp(id2)
disp('(4.3)属于第三类[id3]的样本数据行号：')
disp(id3)
% （5）选取样本数据的前两列（属性）进行绘图，来可视化。
figure(1);
plot(gyzb_data(:,1),gyzb_data(:,2),'r.','MarkerSize',12)
title('样本数据的前两列的散点图：')
xlabel('样本数据的前第一列值');
ylabel('样本数据的前第二列值');
figure(2);
plot(gyzb_data(id1, 1), gyzb_data(id1, 2), 'marker', '*', 'color', 'r');
hold on
plot(gyzb_data(id2, 1), gyzb_data(id2, 2), 'marker', '*', 'color', 'g');
hold on
plot(gyzb_data(id3, 1), gyzb_data(id3, 2), 'marker', '*', 'color', 'b');
title('样本的模糊C均值聚类示意图：')
xlabel('样本数据的前第一列值');
ylabel('样本数据的前第二列值');
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

(3.2)实验截图及分析：

【1】Iteration count 代表迭代次数，观察这组数据，当迭代了24次时，迭代过程中的目标函数趋于稳定时，此时停止迭代，计算出聚类中心、隶属度等结果。但多次测量后每次的迭代次数是不确定的。

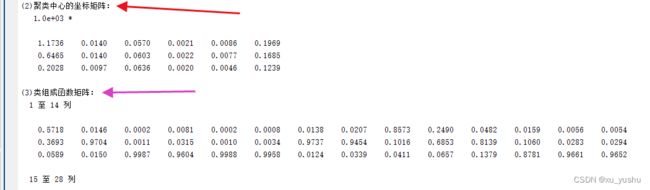
【2】上图为聚类中心的坐标矩阵、隶属度矩阵（类组成函数矩阵）。每组数据对应3个聚类中心的隶属度，第m列代表第m组数据，分别对应四个聚类中心的隶属度值。

【3】上图为多次测试（设置类的数量为3，由于每次测试都是一样，这里就用只显示一张图）的用聚类结果：

属于第一类的5组数据：1，9,15,19,27

属于第二类的8组数据：2,7,8,10,11,17,23,31

属于第三类的18组数据：3,4,5,6,12,13,14,16,18,20,21,22,24,25,26,28,29,30

【4】该图是样本数据的前两列的散点图，由于样本数据不变，因而该图也是趋于不变。

【4】上面这两张图的在不改变类别（簇）的数目，几乎是趋于不变的，（由于每次测试都是一样，这里就用只显示一张图），可见，在设定好同一数目的类别（簇）下，模糊C聚类分析下即使每次迭代次数可能不一样，但结果总是会区于一个稳定值，聚类结果也是趋于一个结果。但聚类结果还是受到研究者所设置的聚类数目的多少等影响，即主观影响大。

3.2 因子分析的实验结果与分析：

（1）实验思路：

数据文件gyzb.mat是一个每一列都是数据值的样本数据矩阵，没有可供判断类别列也没有时间值等。考虑到可选择对gyzb.mat数据文件进行因子分析，加上Matlab有factoran()等自带函数，就开始实验了。

（2）实验步骤：

【1】先导入gyzb.mat数据文件，然后观察数据的大致情况；

【2】选择因子分析；

【3】先在matlab脚本中写好大致的代码思路；

【4】再试着进行编写matlab代码;

【5】对运行得出的结果及统计图进行分析。

（3）结果及分析：

（3.1）matlab代码：

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
disp(' ')
disp('【2】因子分析：')
% （1）导入样本数据
% （2）使用标准化，对样本进行归一化处理, z为标准化后的数据，mu是原样本的均值，sigma是原样本的方差。
z  = zscore(gyzb_data);
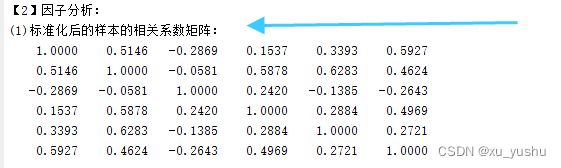
% （3）计算z的相关系数矩阵,r为样本的相关系数矩阵
r = corrcoef(z);
disp('(1)标准化后的样本的相关系数矩阵：')
disp(r)
% （4）设置3个公共因子
number = 3;
% （5）进行因子分析
% 求lambda是因子载荷值；psi是方差构成的向量；T是旋转矩阵；% stats是相关信息统计；F是因子得分矩阵；number是公共因子的数量；
[lambda, psi, T, stats, F] = factoran(gyzb_data, number);
disp('(2) 3个公共因子的情况下：')
disp('(2.1)因子载荷值：')
disp(lambda)
disp('(2.2)方差构成的向量：')
disp(psi)
disp('(2.3)旋转矩阵为：')
disp(T)
% （6）计算贡献率并绘制出柱形图
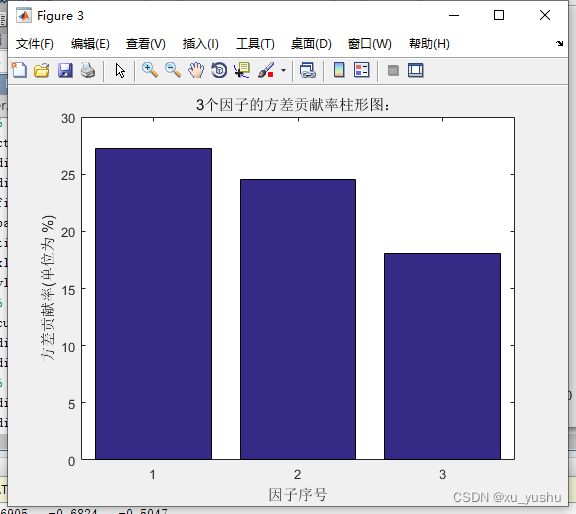
ctb = 100 * sum(lambda .^ 2) / size(gyzb_data, 2);
disp('(3)3个因子的方差贡献率(单位为 %)：')
disp(ctb)
figure(3)
bar(ctb)
title('3个因子的方差贡献率柱形图：')
xlabel('因子序号');
ylabel('方差贡献率(单位为 %)')
% （7）计算累积方差贡献率
cumctb = cumsum(ctb);
disp('(4)因子的累积方差贡献率(单位为 %)：')
disp(cumctb)
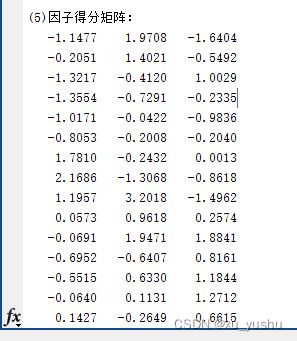
% （8）输出因子得分矩阵 F
disp('(5)因子得分矩阵：')
disp(F)
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

（3.2）实验截图及分析：

【1】由于上下三张图的方差贡献率、累积方差贡献率、旋转矩阵、因子得分矩阵等可见：3个因子的累积方差贡献率为69.8283%，已经超过方差贡献率的2/3，可知因子分析是需要大量数据的，这里大致可以用这3个公共因子（更基本的变量）替代原来的6个变量，来实现降维。

---

4 总结

模糊C聚类分析的结果不是惟一的，受测试者的主观因素算是很大的。样本数据中的异常值和特殊变量对聚类分析的结果影响比较大。由于样本数据量太少，因而因子分析不太合适。一般而言，样本量还是需要为变量数的10倍以上。但两种分析方法都相互表意了这个数据文件gyzb.mat是可以进行压缩的。即对行进行归类，对列进行抽出公共因子。

---

参考文献

Matlab的模糊聚类分析的传递方法》，计算机应用，2004.11

郭珉，《模糊聚类分析算法的Matlab语言实现》，农业网络信息，2004.5

由伟、刘亚秀，《MATLAB数据分析教程》，清华大学出版社

李柏年、吴礼斌，《MATLAB数据分析方法》，机械工业出版社