学习笔记-3-SVM-5-Approximate LSVM
细节内容请关注微信公众号:运筹优化与数据科学
ID: pomelo_tree_opt
Outline
1. Linear separable?
2. Approximate LSVM - basic idea
3. Piecewise-linear minimization
4. Approximate LSVM implication
5. Approximate LSVM considering generalizability
----------------------------
1. Linear separable?
Linearly separable?
-
How do we know a given dataset is linearly separable?
-
How difficult to check the linear separability
--------------------------------
前面的例子,都是hard margin的例子,是对一堆数据直接解primal or dual LSVM.
现在的问题是给了一堆数据之后,我们并不知道是否是线性可分的。
二维的还可以勉强观察一下,三维的基本上就看不出来了,更高维的更没戏。
----------------------------
问题是我们怎么判断给定的这一堆数据是否是线性可分的?
第一个思路就是,不管是不是线性可分的,直接丢到solver里,去解primal or dual LSVM, 看看是不是feasible.
-
如果feasible, 就是线性可分的,而且直接得到了分割超平面。
-
如果不是线性可分的,就是infeasible, 压根解不出来。
注意这是通过解一个quadratic programming来判断是否是线性可分。
那么有没有更简单的方式来判断究竟是不是linearly separable呢?
---------------------------
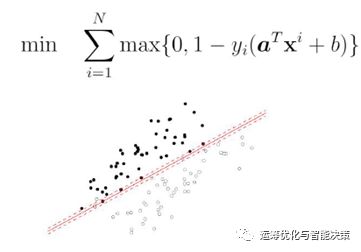
再进一步,所以可以有个penalty function, 来惩罚那些违反约束的点。
=========================
2. Approximate LSVM - basic idea
注意,max的部分才是penalty.
-
如果违反了约束就罚,就是1-y_i(a^T x^i + b)的部分
-
如果没违反,就不罚,也即是罚0.
然后把所有的violation加起来,就是sum的部分,然后去minimize这个sum的东西。
最终是找到合适的a和b,使得total violation越小越好。
----------------------------------
这就是approximate linear separation.
我们还是在找a和b,找到了a和b,就找到了一个hyperplane.
这个就叫做approximation LSVM.
----------------------------------
而且这个问题的特点是,这个问题永远都是feasible的,因为压根没有任何restriction,也就是没有约束条件。一定会得到a和b. 与之前的primal LSVM或dual LSVM相比,这两个如果丢给solver,很可能是infeasible的。
-
如果obj=0, 意味着能顺利找到一个分割超平面,e.g. H2与H3,意味着真的是linear separable, 而且是真的给了个supporting hyperplane, 至于这个supporting hyperplane有多好是另外一码事,比如这里给的H2,而primal LSVM给的是H3.
-
如果obj不为0,说明是线性不可分的,至少有一个点violation. 但是这也能给我一个a和b,告诉我们这个a和b构造的分割超平面已经是不错了。
----------------------------------
这个function有时候叫做hinge-error function,就是强调这个hyperplane是approximate的,会有些点在超平面附近错落摆放,所以是hinge. 只是个名词而已。
----------------------------------
A piecewise-linear minimization problem with variables a, b.
第三个是无约束的,如果目标函数是convex的,那么local optimum就是global optimum. N个东西加起来的,如果每个东西都是convex的,那么加起来还是convex的。事实上每个里面的东西都真的是convex的,所以总体就是convex的。
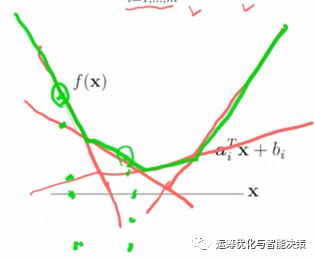
里面两部分,0可以看作是个线性的东西,1-y_i(a^T x^i + b)也是个线性的东西,两个线性的东西取大,就是max的操作,得到的是个凸函数。正常情况下对于一个convex的东西,要想求max或min,令derivative为0即可,就是导数为0.
问题是有个拐点,不是differentiable,不光滑、不可微。就是下面的样子
=========================
3. Piecewise-linear minimization
Nondifferentiable的piece-wise linear的东西处理起来难吗?一点都不难。
minimize一个piecewise linear的东西等价于解一个LP问题,是容易问题
-------------------------------------
这是做optimization常用的手法
-
原来是个无约束的、non-linear, non-differentiable的东西,因为是non-differentiable,所以不能上导数那些。
-
现在是个LP问题,有n+1个变量,m个约束条件,(这是个容易问题)。
-------------------------------------
再回到我们原来的问题
把这个approximate linear SVM转变后的LP问题跟primal LSVM对比下
原来的primal LSVM是n+1个变量,N个约束,是凸二次规划
现在的LP是n+1+N个变量,N个约束,是线性规划
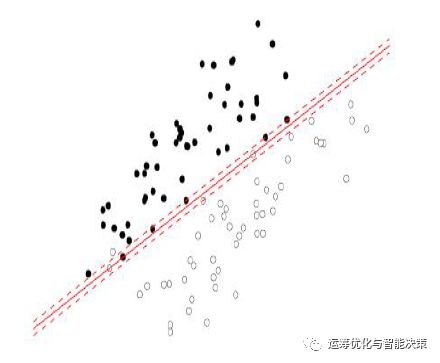
这个approximate LSVM就是不管是否是linearly separable or not, 都可以得到一个support hyperplane, 允许有一定的violation
=========================
4. Approximate LSVM implications
可以试试给定一堆线性可分的数,分别用primal LSVM or dual LSVM,以及approximate LSVM的piece-wise linear来处理,比较得到的结果。
基本认识是primal LSVM的东西得到的结果generalizability要好,留有余地
而piece-wise linear的东西是今天做好就好,留有的余地远远没有primal LSVM要多。
另外一个思路,可以先通过解piece-wise linear的东西来判断是否linearly separable,如果为0的话,再去解一个primal LSVM或dual LSVM. 解两次就好了。
这样做两次肯定是可以的。但是更重要的是要在这里引入另外一个概念soft margin SVM. 一个好的approximate LSVM,就是linear soft SVM, 即LSSVM.
=========================
5. Approximate LSVM considering generalizability
不同的C会得到不同的解,这是在直觉上分析C,不是数学上分的分析。
学machine learning并不是在学数学,有很多东西需要动手练习,才能逐渐了解具体是在做什么。而且得到的永远是engineer solution, 并不是mathematical solution.