《速通机器学习》-第六章 无监督学习

本书前面提到的各种模型，无论是回归还是分类，在训练阶段都有一个共同的前提条件，即需要有标注的训练样本。标注数据会告诉模型，“对这条数据，输入 x 后，我想要结果 y”。模型会根据要求，使用梯度下降法或其他求解方式，不断调整自身参数，使输出 y^' 尽可能接近标注 y。这类学习统称为有监督学习。标注 y 就是监督信号（也称为教师信号），用于告诉模型数据 x 所对应的正确类别 y。在企业中，标注数据的来源一般是人工标注，以及收集的用户反馈信息。

不过，现实很“残忍”。在互联网时代，企业每天都会产生海量的数据，人工标注的速度不可能赶上数据产生的速度。这就意味着大部分数据缺少人工标注，无法用于有监督学习。尽管我们可以通过收集日志的方法（例如收集用户点击日志或其他用户行为信息）获取有标注的训练样本，但这其实是把标注任务“外包”给了用户，用户获得的“报酬”是免费使用产品。

日志法固然好，但有局限性，例如产品刚上线时没有日志数据可用。另外，需要考虑作弊因素，即被注入的无效数据（这会导致训练样本不准确，训练出来的模型效果不好）。还有一些分类需求，用户需要的是分类结果，但不会提供标注数据，例如资讯类App需要把新闻等文章放入不同的频道以提供给不同的用户，这时就无法利用用户信息了。还有一些场景，例如图像识别、语音识别，标注数据尤其昂贵，甚至催生出一条数据产业链，诞生了不少知名公司。

面对没有标注数据可用的现状，算法工程师们只能感叹“巧妇难为无米之炊”。然而，绝望往往是滋生希望的土壤，针对大量的无标注数据，出现了一系列专门处理这类问题的模型。这些模型不需要使用标注数据（也就是说，只需要 x，不需要 y），而是利用数据自身的分布特点、相对位置来完成分类。这类模型称为无监督学习（y 可以理解成监督信号）或自组织模型。

下面我们从常用的无监督模型K-Means开始探讨无监督学习。

6.1　K-Means聚类

6.1.1　K-Means算法的基本原理

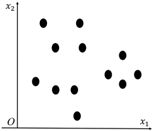
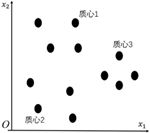
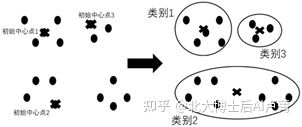
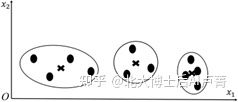
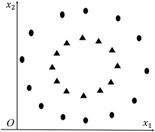
有一批无标注数据，数据点在空间中的分布，如图6-1所示。我们现在希望利用这些数据自身的分布特点自动进行聚类。在这里使用了一种朴素的思想：如果两个数据点的距离比较近，那么它们的类别就应该是一样的。同理，如果一堆数据点彼此接近，那么它们的类别也应该是一样的。于是，将这堆数据点的质心作为这个类别的代表，如图6-2所示。

图6-1

图6-2

需要注意的是：质心点在大部分情况下不是一个真实的数据点。

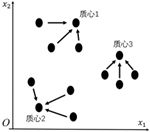
下面讨论一下如何使用以上朴素的思想对数据进行自动聚类。在无监督学习中，一般可以根据过往经验（拍脑袋）设置一个类别数 K（表示我们希望这堆数据中有多少个类簇）。在训练数据中随机挑选 K=3 个点作为各个类簇的质心，如图6-3所示。对剩下的数据点，分别计算它们和这3个类簇的质心之间的距离。在这里采用欧氏距离，每个点都将归入与它距离最近的类别，如图6-4所示。

图6-3

图6-4

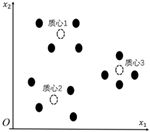
对每个类别来说，一开始质心都是随机挑选的。现在，每个类别都有了一堆数据。对每一类数据的所有点求平均值，将平均值作为新的质心，会产生 K=3 个新的质心，如图6-5所示。

图6-5

定义损失函数 Loss=∑_(i=1)^K▒∑_(x_((j))∈cluster_i)▒〖||x_((j)),μ_i ||〗。K 为类簇数。μ_1~μ_K 表示各类簇的

质心。Loss 的含义是所有数据点 x_((j)) 到它所属类簇的质心 μ_i 的欧氏距离之和。模型训练过

程就是寻找最优的参数 μ_1~μ_K，使得 Loss 最小，而此时也能得到 x_((j)) 所属的类簇。但是，

x_((j))∈cluster_i 的出现将导致 Loss 是一个不连续函数，所以无法直接求解 ∂Loss/(∂μ_i )。不过，我们

可以使用EM算法（Expectation-Maximization Algorithm）来学习 μ_1~μ_K，步骤如下。

 根据经验和业务特点设置类簇数 K，即在所有数据中随机选择 K 个点作为质心 μ_1~μ_K。

 对数据点进行分类，使训练数据中的每个样本都归入与其距离最近的质心所代表的类

别。对于训练样本 x_((j))，其类别为 k=〖arg ( min)┬i〗⁡〖||x_((j)),μ_i ||〗，即 x_((j))∈cluster_k。

 对于类别 i（i=1,⋯,K），用第步的分类结果重新计算质心，也就是求每个类别中样本的平均值，公式如下。

μ_i=1/N_i ∑_(x_((j))∈cluster_i)▒x_((j))

N_i 为归入 cluster_i 的样本数量。

 对以下3个条件进行判断。如果其中任何一个被满足，就可以结束聚类。否则，返回第步。

没有（或最小数目）对象被重新分配给不同的聚类。

没有（或最小数目）聚类中心再发生变化。

Loss=∑_(i=1)^K▒∑_(x_((j))∈cluster_i)▒〖||x_((j)),μ_i ||〗 足够小。

聚类完成后，训练样本中的每个数据点 x_((j)) 都将有一个明确的类别 i（i=1,2,⋯,K）。质心 μ_1~μ_K 用于对非训练样本中的数据进行预测。一个数据点和哪个质心的距离最近，它就属于哪一类，即

k=〖arg min┬i〗⁡〖||x,μ_i ||〗

也就是 x∈cluster_k。

K 是一个超参数，是通过我们的经验设置的。K 越大，分类就越精细；K 越小，分类就越粗糙。上述方法称为K-Means，“K”代表设置的类别数，“Means”（均值）表示在以上第步求质心时使用的平均值。

K-Means算法的结果符合丑小鸭定理——数据是否在一个类簇中并无客观标准，数据是否会聚在一起，完全取决于提取出来的特征。如果特征为蛋白质含量、口感之类，那么鱼和螃蟹就可以归为一类；如果特征为生物学特征，例如有无脊柱、腿的数量之类，那么鱼和螃蟹显然会被分配到不同的类别。因此，特征提取方法隐式地表达了分类标准。

另一个值得注意的要点是，K-Means算法是以欧氏距离为基础的。我们在5.4节讨论维数灾难时提到过，当特征维度过高时，欧氏距离就会失效。因此，在使用K-Means算法时，特征维度不宜过高。

6.1.2　改进型K-Means算法

尽管K-Means算法足够简单，性能也不错，但仍有不少缺点。

K-Means算法对初始点比较敏感。尽管初始点是随机选取的，但选取不同的初始点会对最终的聚类结果产生影响，如图6-6和图6-7所示。

对初始点敏感意味着K-Means算法容易被随机选取的初始点影响，从而使同样的数据产生多种聚类结果。这些结果到底哪个更好呢？对同一批数据，可以重复使用K-Means算法，

每次选取不同的随机初始点，最后将 Loss=∑_(i=1)^K▒∑_(x_((j))∈cluster_i)▒〖||x_((j)),μ_i ||〗 最小的聚类结果作

为最终结果。

图6-6

图6-7

上述算法在数据量很大时往往不够经济，花费的时间和计算成本较高。因此，有人提出了K-Means++ 方法，在选择初始点方面对K-Means方法进行了改进，步骤如下。

 从 N 个数据点中随机选择一个作为类的中心。初始点为 μ_1。

 计算各数据点到已有的聚类中心的距离，并将各样本归入与其距离最近的聚类中心所

在的类别（如果只有初始的一个类别，那么所有样本都归为一个类簇）。对于样本 x_((j))，类

别为 (arg min)┬(i=1,2,⋯,k)⁡〖||x_((j)),μ_i ||〗，k 为当前类簇数。

 计算各数据点到其所属类簇中心的距离 ||x_((j)),μ_i ||。选择距离最远的数据点，将其作

为新的聚类中心 μ_(k+1)，即

μ_(k+1)=(arg max)┬█(x_((j) )∈cluster_i@i=1,⋯,k)⁡〖||x_((j)),μ_i ||〗

 重复第步和第步，直至获得 K 个聚类中心为止。然后，将这 K 个聚类中心作为初始聚类中心，重新执行前面的K-Means算法流程。

K-Means++ 找寻初始质心的原则为：各类簇的质心尽可能相互远离，从而为质心的确定提供客观标准。K-Means++ 的运算量不大，没有随机过程，在实际应用中是一种有效的改进方法。

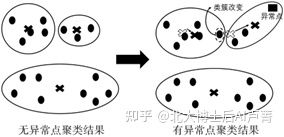
K-Means算法在训练数据的过程中，有时会遇到异常点，如图6-8所示。

图6-8

异常点的出现，会使类簇的质心发生偏移，从而影响最终的效果。针对这个问题，有两个常用的解决方法，具体如下。

第一个方法是，归类完成后，在一个类簇中计算各个点到同一类簇的其他点的平均距离。如果一个点到同一类簇的其他点的平均距离较大，就意味着该点偏离这个类簇中的大多数点，在计算类簇的质心时可将该点作为异常点剔除。

第二个方法是，将质心为类簇内所有点的平均值改为中位数（中位数不容易受极端值的影响）。

若数据点中第 x_1 维特征的变化量远大于其他维，则数据点的分布基本仅由第 x_1 维的特征决定，其他特征的影响很小，如图6-9所示。

图6-9

可以看出，特征 x_2 对聚类结果基本没有影响。该问题的解决方法是：参考逻辑回归，对数据点特征进行归一化，使各个维度的幅度保持一致。

在K-Means算法中，K 一般根据经验来设置，具有一定的主观性。

有一种方法可以客观地确定 K。假设有 N 个数据点，K 的取值范围是 1~N。K 越大，

分类就越细，Loss=∑_(i=1)^K▒∑_(x_((j))∈cluster_i)▒〖||x_((j)),μ_i ||〗 就越小。因此，随着 K 的增大，Loss 会不

断减小，但减小的幅度会越来越小，即 K 增大的边际收益越来越小。当这个边际收益小到一定程度时，就认为增大 K 的意义不大了，将此时的 K 作为分类结果。

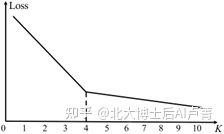
K-Loss 关系图，如图6-10所示。

图6-10

当 K<4 时，随着 K 的增大，Loss 的下降速度加快，说明增大 K 的收益是显著的。当 K ≥ 4 时，Loss 的下降速度放缓，说明增大 K 的收益是不显著的。所以，K=4 就是最佳类别数。

有一种情况是K-Means算法无法解决的，即数据点组成两个同心圆，如图6-11所示。

图6-11

此时，我们希望椭圆形为一个类簇，三角形为另一个类簇。但是，直接使用K-Means算法无法聚类成理想的结果。其原因在于，K-Means算法基于一个假设，即在使用欧氏距离进行度量时，同一类别的数据点彼此接近，而同心圆中的数据分布显然不满足这种假设——前提条件不成立，后面的推理都会失败。

为了解决这个问题，可以使用特征转换的方法，将所有数据点 x_((i))=〖[x_((i),1),x_((i),2)]〗^T 转换

成点与圆心的距离 [〖(x〗_((i),1)-r_1 )^2+〖(x_((i),2)-r_2)〗^2]，即将2维特征转换成1维特征。尽管特征

维度变小了，但问题得到了解决。这也说明，使数据和模型相匹配比单纯增加维度更有效。

6.1.3　K-Means算法和逻辑回归的结合应用

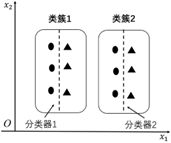
K-Means算法不仅可以用在聚类上，它和逻辑回归相结合，还能使分类效果得到提升。如图6-12所示，三角形为一类，椭圆形为一类。显然，这是一个线性不可分的数据分布。

图6-12

要想让逻辑回归在线性不可分时有效，就必须对特征进行修改。除了5.5节介绍的维度扩增方法，还可以用K-Means算法辅助完成逻辑回归。首先，忽略标签数据，使用K-Means算法对数据点进行聚类。然后，对每个类簇单独使用一个逻辑回归分类器进行分类。虽然数据整体是线性不可分的，但使用K-Means算法将数据分成两个类簇后，每个类簇中的数据就都是线性可分的了，如图6-13所示。

图6-13

在训练阶段，每个类簇中的数据都对应于一个独立的分类器，每个分类器都使用该类簇的标注数据进行训练。在预测阶段，可先找到输入 x 所对应的类簇 k，再使用该类簇所对应的分类器进行分类。

在一些较为复杂的数据分布中，可以尝试“先对数据进行聚类，再对各类簇单独进行分类”的策略。虽然数据整体情况复杂，但具体到某个类簇，数据的复杂度将会降低。此时，对每个类簇单独训练分类器（不限于逻辑回归），往往能取得不错的效果。

6.2　主题模型

人工智能有一个非常大的应用落地领域，就是自然语言处理。目前市面上的诸多产品，例如推荐系统、搜索系统、对话系统等，都是自然语言处理应用的主战场。

在自然语言处理领域，内容理解是一个重要的方向。内容理解常使用主题（Topic）表示一篇文档的风格和领域倾向，例如“数学”“哲学”都可以作为文档的主题。同时，一篇文档往往不止有一个主题。例如，一篇讨论机器学习的文档，有30% 的主题为“数学”，有70% 的主题为“计算机”。这种以概率形式描述文档在各主题上占比的方法称为主题分布。

文档的主题可以使用分类模型进行预测，但在预测前，需要由领域专家确定文档的主题分布，并收集一批标注了主题的训练样本来训练模型。这是一项需要耗费大量人力的工作，特别是领域专家确定主题分布，是一项见仁见智的工作，没有客观标准。

LDA（Latent Dirichlet Allocation）模型用于推测文档的主题分布，可以将一个文档集中每篇文档的主题以概率分布的形式给出。主题分布可以作为文档的特征，用于文本相似度计算或后续的分类任务。不同于文本分类，LDA是无监督模型，不需要标注数据，模型可以自动从文档集中推测文档所属的主题，且主题本身是通过模型学习得到的，不需要人工设定。

LDA是自然语言处理领域的一个成熟的模型，有严谨的数学理论作为支撑，应用广泛。下面我们来一探LDA的究竟。

6.2.1　LDA模型的原理

在处理文本时，提取文本特征最直接的方式是使用multi-hot编码。

假设词库中有a、b、c、d、e、f、g、h、i、j共10个词，每篇文档都有一个10维的特征向量。如果在一篇文档中，词a出现了两次，词b、e、f各出现了一次，那么这篇文档可以用向量 〖[2,1,0,0,1,1,0,0,0,0]〗^T 来表示。不过，这种方法有很多缺点，列举如下。

汉语的常用词有约20万个，意味着向量长度约为200000，而一篇文档中可能仅出现几百个词，multi-hot向量中会出现大量的0，非常稀疏。

没有考虑词的顺序问题。例如，“我借给你钱”和“你借给我钱”这种意思相反的句子，其multi-hot向量却是一模一样的。

中文的语义歧义问题。例如，“苹果手机”和“吃苹果”中的“苹果”是完全不同的事物，但它们所对应的特征是一样。

对同一事物，表述方法的差异可能很大。例如，“电脑”和“计算机”虽然描述的是同一事物，但对应于不同的特征，因此它们所对应的multi-hot向量的差异很大。

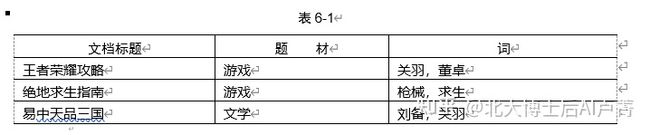
通过以上分析可以发现，multi-hot作为文档的特征向量，存在很多缺点。例如，有三篇文档，如表6-1所示。

表6-1

理想的特征向量应该具备如下特点。

在差异较大的文档（例如《王者荣耀攻略》和《易中天品三国》）中，向量有较大的差异。

相似的文档（例如《王者荣耀攻略》和《绝地求生指南》），向量相似。

向量维度不宜过高，以便进行后续运算。

需要注意的是，相似的文档中词的差异可能比较大，而差异较大的文档中可能有很多共现词。如表6-1所示，从内容的角度看：前两篇文档比较接近，都是关于游戏的，但它们的共现词很少；第三篇文档和前两篇文档几乎没有关系，但如果只看词，就会得到第一篇文档和第三篇文档内容相似的（错误）结论。可见，将词作为文档的特征，不仅有高维空间带来的难度，也有使用时的错误，因此，需要换一种思路，用其他特征来表示文档。

在一篇文档中，词只是“表面现象”，词的背后是一个个主题，它们代表了文档的风格、领域等。站在作者的角度，在写一篇文档前都会构思主题，例如“数学”“计算机”“文学”。主题有时未必能准确地对应到现实概念中具体的一个类。主题往往是抽象（隐式）的，例如“计算机偏数学”“计算机偏编程”这种客观存在但很难用确切的概念来描述的主题。

一篇文档可能对应于多个主题，例如《速通机器学习》70% 属于“计算机”主题，30% 和“数学”沾亲带故；每个主题都以特定的概率分布与词对应，例如在“计算机”主题中，“算法”“神经网络”之类的词会以较大的概率出现，而在“数学”主题中，“公式”“导数”等词出现的概率将高于其他词。需要注意的是，同一个词可以出现在不同的主题中，例如“梯度”可以出现在“计算机”“数学”两个主题中，只不过对应的概率有所不同。

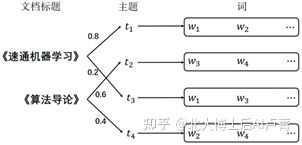
接下来，我们讨论一下如何以主题的方式写一篇文档（这里的文档简化为词袋模型）。词袋模型忽略文档中词之间的顺序，只关心文档中有哪些词，就像把所有词一股脑装进一个袋子里一样。首先，需要确定文档的主题分布，例如《速通机器学习》分别以20% 和80% 的概率对应于主题 t_1 和 t_2。然后，根据上述主题概率选择相应的主题，例如选择 t_1，那么 t_1 就根据其所对应的词的分布生成文档中的一个词 w_1。接下来，重新选择文档主题并生成新的词。上述过程进行 N 次，就得到了一篇有 N 个词的文档。用同样的方法生成文档《算法导论》，其所对应的主题分布与文档《速通机器学习》不同。上述过程，如图6-14所示。

通过以上分析可知，所有文档共同对应于 K 个主题和 V 个词，不同文档的主题分布不同。因此，可以将写作过程类比为轮流投掷两类骰子的过程。

第一类骰子 P_doc (Topic=t|Doc=m) 表示第 m 篇文档的主题为 t 的概率。有 M 篇文档，就有 M 个骰子（m=1,2,3,⋯,M），每个骰子有 K 个面（主题数，t=1,2,3,⋯,K）。风格差异较大的文档，对应的 P_doc (Topic|Doc) 分布不同。

对每个主题 t，生成词 w 的概率为 P_topic (Word=w|Topic=t)，即第二类筛子。有

K 个主题，就有 K 个骰子（k=1,2,3,⋯,K），每个骰子有 V 个面（词数，w=

1,2,3,⋯,V）。P_topic (Word|Topic=1) 和 P_topic (Word|Topic=2) 可以反映 t_1 和 t_2

之间的差异。

图6-14

假设文档 m 中有 N 个词，写作过程如下。

 投掷主题筛子 P_doc (Topic=t|Doc=m)，得到一个确切的主题 t。

 根据第步得到的主题 t，投掷主题筛子 P_topic (Word=w|Topic=t)，生成具体的词 w。

 重复上述过程 N 次。

在这里，需要注意以下两点。

在一篇文档中，如果某个词 w 出现的次数较多，那么可能是由不同的主题骰子（例如 P_topic (Word=w|Topic=1) 和 P_topic (Word=w|Topic=2)）投出的。

以上例子使用词袋模型处理文档，忽略了词出现的顺序。尽管词袋模型和真实的写作过程有一定的差异，但它能够大大降低模型的复杂度。

在上述过程中，我们并不知道两类骰子的具体分布。下面就通过机器学习了解一下隐藏在文档后面的这两类骰子。

6.2.2　LDA模型的训练

在正式讲解LDA模型的训练之前，我们来定义一些符号。z_i=t（i=(m,n)，是一个二维下标）表示第 m 篇文档的第 n 个词所对应的主题 t，它所对应的词为 w_i=w（w 是一个具体的词，例如“苹果”“算法”）。所有文档一共对应 V 个词和 K 个主题。K 是一个超参数，需要人工设置（类似于K-Means算法里的类别数）。

在语料（M 篇文档）中，w_i=w 是第 m 篇文档的第 n 个词，这是一个已知的客观事实。但是，我们并不知道该词所对应的主题 z_i。LDA模型的学习过程就是求解 z_i 的过程。

为文档中的每个词随机赋予一个主题。例如，z_((1,1))=1，z_((1,2))=3，z_((2,1))=2。在这里，主题只是一个编号，并无大小之分。我们可以得到以下两类计数。

n_m^t 表示第 m 篇文档中对应主题为 t 的词数，n_(m,¬i)^t 表示剔除词 i=(m,n) 后的词数。

n_t^w 表示所有文档中对应主题为 t 的词 w 的数量，n_(t,¬i)^w 表示剔除词 i=(m,n) 后的词数。

为了准确地得到 z_i 所对应的主题，可使用 z_(¬i) 和 w_(¬i)（除 i=(m,n) 外的所有词和对应的主题）来估计 z_i=t 的概率。

首先，不难发现

P(z_i=t|z_(¬i),w_(¬i) )∝P_doc (Topic=t|Doc=m)P_topic (Word=w|Topic=t)

这个式子不难理解，意思是 z_i=t 的概率和以下二者成正比。

主题 t 在第 m 篇文档中出现的概率，表示文档的整体风格。

词 w_i=w 在主题 t 上出现的概率，表示主题 t 的选词倾向。

直接用频率来估计概率，即

P_doc (Topic=t│Doc=m)=(n_(m,¬i)^t)/(∑_(t^'=1)^K▒n_(m,¬i)^(t^' ) )

在这里使用 n_(m,¬i)^k 而不使用 n_m^k 的原因在于，需要使用除词 i=(m,n) 外的所有词来估计 z_i

的概率分布。

为了使函数平滑一些，避免在词的数量过少时出现估计偏差，上式可以改进为

P_doc (Topic=t│Doc=m)=(n_(m,¬i)^t+α_t)/(∑_(t^'=1)^K▒〖〖(n〗_(m,¬i)^(t^' )+α_(t^' ))〗)

α_t 为先验超参数，表示第 m 篇文档在训练样本之外有 α_t 个词属于主题 t。

使用同样的方法，可以得到

P_topic (Word=w│Topic=t)=(n_(t,¬i)^w+β_w)/(∑_(w^'=1)^V▒〖〖(n〗_(t,¬i)^(w^' )+β_(w^' ))〗)

β_w 为先验超参数，表示在训练样本之外有 β_w 个词 w 所对应的主题为 t。

完成 P_doc (Topic=t│Doc=m) 和 P_topic (Word=w|Topic=t) 的估计后，我们看一下如何确定 z_i 所对应的主题。假设有3个主题（K=3），w_i=“导数”，使用上述估计方法，得到 z_i 在 t=(1,2,3) 上的概率（得分），公式如下。

{█(P_doc (Topic=1│Doc=m)=0.2 @P_topic (Word=“导数”│Topic=1)=0.1)┤⟹P(z_i=1|z_(¬i),w_(¬i) )∝0.2×0.1=0.02

{█(P_doc (Topic=2│Doc=m)=0.3 @P_topic (Word=“导数”│Topic=2)=0.3)┤⟹P(z_i=2|z_(¬i),w_(¬i) )∝0.3×0.3=0.09

{█(P_doc (Topic=2│Doc=m)=0.5 @P_topic (Word=“导数”│Topic=3)=0.2)┤⟹P(z_i=3|z_(¬i),w_(¬i) )∝0.5×0.2=0.1

那么，z_i=1、z_i=2、z_i=3 就以0.02∶0.09∶0.1的比例进行概率采样得到。采样结束后，词 i 就有了一个明确的主题，例如 z_i=2。用上述方法遍历文档中的词，每个词都会重新对应于一个主题，即 z_((1,1))=2、z_((1,2))=3、z_((2,1))=1……当所有词的主题更新完毕，就完成了一次迭代。

LDA的训练过程是就是重复上述过程，直至每个词所对应的主题不再发生变化（或者变化较小，或者完成一定的迭代次数）为止，具体如下。

 选择合适的主题数 K（超参数，通常根据经验确定），并为训练样本中的词随机分配一个主题，例如 z_i=2。

 遍历文档中的词 z_i（i=(m,n)），计算 z_i 在各个主题上的得分，然后根据得分进行主题采样，更新 z_i 所对应的主题。得分的计算公式如下。

P(z_i=t|z_(¬i),w_(¬i) )∝P_doc (Topic=t│Doc=m) P_topic (Word=w|Topic=t)

其中

P_doc (Topic=t│Doc=m)=(n_(m,¬i)^t+α_t)/(∑_(t^'=1)^K▒〖〖(n〗_(m,¬i)^(t^' )+α_(t^' ))〗)

P_topic (Word=w│Topic=t)=(n_(t,¬i)^w+β_w)/(∑_(w^'=1)^V▒〖〖(n〗_(t,¬i)^(w^' )+β_(w^' ))〗)

将 z_i 所对应的主题按下述方式进行采样。

P(z_i=1|z_(¬i),w_(¬i) ),⋯,P(z_i=K|z_(¬i),w_(¬i) )

主题采样完成后，每个词都能对应于一个具体的主题，例如 z_i=2。

 当每个词所对应的主题不再发生变化（或者变化较小，或者迭代达到一定次数）时，结束训练。否则，返回第步，重新估计每个词所对应的主题。

训练完成后，每个词都会对应于一个主题。因为进行了多次迭代运算，所以，每个词都会被赋予一个较为合理的主题（相对于一开始的随机分配），n_m^k 和 n_k^t 的值也会稳定下来。

一篇文档可以由其所在的主题分布来表示。假设有 K=3 个主题，对于第 m 篇文档

P_doc (Topic=1│Doc=m)=(n_m^1+α_1)/(∑_(t^'=1)^K▒〖〖(n〗_m^(t^' )+α_(t^' ))〗)=0.2

P_doc (Topic=2│Doc=m)=(n_m^2+α_2)/(∑_(t^'=1)^K▒〖〖(n〗_m^(t^' )+α_(t^' ))〗)=0.3

P_doc (Topic=3│Doc=m)=(n_m^3+α_3)/(∑_(t^'=1)^K▒〖〖(n〗_m^(t^' )+α_(t^' ))〗)=0.5

那么，第 m 篇文档可以由向量 [0.2,0.3,0.5]^T 来表示。

在训练LAD模型时，除了能得到每篇文档的主题，还能得到词 w 在主题 t 上的概率分布，也就是 P_topic (Word=w│Topic=t)。

P_topic (Word=w│Topic=t) 是在所有文档上的全局概率分布，即

P_topic (Word=w│Topic=t)=(n_t^w+β_w)/(∑_(w^'=1)^V▒〖〖(n〗_t^(w^' )+β_(w^' ))〗)

其中

t=1,2,⋯,V k=1,2,⋯,K

训练完成后，训练样本中的每篇文档都会有一个对应的主题。那么在推断阶段，拿到一篇新文档 m+1，应该如何得到其主题分布呢？训练完成后，P_topic (Word=w│Topic=t) 就不再变化了，我们需要推断的只是 P_doc (Topic=t│Doc=m+1)，步骤如下。

 给新文档中的每个词随机分配一个主题。

 遍历新文档中的词 z_i（i=(m+1,n)），计算 z_i 在各个主题上的得分，然后使用得分比例采样得到 z_i 所对应的主题。z_i=k 的得分的计算公式如下。

P(z_i=k|z_(¬i),w_(¬i) )∝P_doc (Topic=t│Doc=m+1) P_topic (Word=w│Topic=t)

其中

P_doc (Topic=t│Doc=m+1)=(n_(m+1,¬i)^t+α_t)/(∑_(t^'=1)^K▒〖〖(n〗_(m+1,¬i)^(t^' )+α_(t^' ))〗)

P_topic (Word=w│Topic=t) 为训练过程中得到的结果，无须再次计算。

 重复第步，直至模型稳定。

模型稳定后，新文档中的每个词都会对应于一个主题。因此，可使用 n_(m+1)^t 计算新文档的主题分布，公式如下。

P_doc (Topic=1│Doc=m+1)=(n_(m+1)^1+α_1)/(∑_(t^'=1)^K▒〖〖(n〗_(m+1)^(t^' )+α_(t^' ))〗)=0.3

P_doc (Topic=2│Doc=m+1)=(n_(m+1)^2+α_2)/(∑_(t^'=1)^K▒〖〖(n〗_(m+1)^(t^' )+α_(t^' ))〗)=0.4

P_doc (Topic=3│Doc=m+1)=(n_(m+1)^3+α_3)/(∑_(t^'=1)^K▒〖〖(n〗_(m+1)^(t^' )+α_(t^' ))〗)=0.3

最终，新文档可以由向量 〖[0.3,0.4,0.3]〗^T 来表示。该向量中的每个元素都表示对应位置的主题的强度。

LDA使用主题特征对文档进行表示，具有以下优点。

文档主题是一种深层语义。对于两篇文档使用的词差异很大，但对应的主题分布类似的情况，LDA在计算文档相似度时效果更好。

在处理文本时，相比one-hot编码，主题数 K 一般不会特别大（在中文文档中一般是128～256），从而使文档的特征更加稠密且节省空间。

可以在一定程度上解决一词多义的问题。例如，文档A讲苹果种植，文档B讲苹果手机发布。在文档A中，大部分词与农业有关，P_doc (Topic=“农业”│Doc=文档A)=0.8（较大），词“苹果”会以较大的概率对应于“农业”主题。而在文档B中，词“苹果”所对应的主题是“科技”。

LDA是一个词袋模型，因此，如果场景对词出现的顺序（词序）比较敏感，那么LDA并不适用。所幸在大部分场景（例如文本分类、文本相似度计算）中，词序对结果不会有太大的影响。

LDA在企业中应用广泛，能够对文档进行深层次的语义表示，几乎成为自然语言处理工程师绕不开的技术。随着行业的发展，LDA开始应用在其他领域，举例如下。

在短视频推荐系统中，需要建立用户画像。可以把一个用户当作一篇文档，把用户看过的视频的ID当作词，使用LDA技术把一个用户的观影风格转换成一个主题向量。

一篇较强专业性的文档一般会重点阐述一个知识点，主题分布则集中在少量主题中。因此，可以通过计算主题分布的信息熵来量化文档的专业性。例如，在推荐系统中，可以在垂直频道推荐一些专业性较强的文档，而对缺乏了解的新用户，则推荐一些娱乐新闻类文档。

在推荐系统中，LDA既可用于非个性化的推荐，也可作为内容特征进行内容召回（作为新用户行为特征不足时的补充）。

---

对机器学习感兴趣的读者可以去主页关注我；本人著有《速通深度学习》以及《速通机器学习数学基础》二书，想要完整版电子档可以后台私信我；实体版已出版在JD上有售，有兴趣的同学可以自行搜索了解

想一起学习机器学习的话也可以后台私信，本人所做机器学习0基础教程已有60余章还未公开；想了解的话也是后台私信或者评论区留言。