【学习11】Spatial Transformer Layer

1、Spatial Transformer Layer

不变性

不变性意味着即使目标的外观发生了某种变化，但是依然可以把它识别出来。这对图像分类来说是一种很好的特性，因为我们希望图像中目标无论是被平移，被旋转，还是被缩放，甚至是不同的光照条件、视角，都可以被成功地识别出来。

平移不变性：Translation Invariance
旋转/视角不变性：Ratation/Viewpoint Invariance
尺度不变性：Size Invariance
光照不变性：Illumination Invariance

为什么CNN有transition invariant?

局部平移不变性是一个很有用的性质，尤其是当我们关心某个特征是否出现而不关心它出现的具体位置时。

在神经网络中，卷积被定义为不同位置的特征检测器，也就意味着，无论目标出现在图像中的哪个位置，它都会检测到同样的这些特征，输出同样的响应。比如人脸被移动到了图像左下角，卷积核直到移动到左下角的位置才会检测到它的特征。

简单地说，卷积+最大池化约等于平移不变性。即为参数共享和池化使卷积神经网络具有一定的平移不变性。

 卷积神经网络CNN

神经网络由大量的神经元相互连接而成。每个神经元接受线性组合的输入后，最开始只是简单的线性加权，后来给每个神经元加上了非线性的激活函数，从而进行非线性变换后输出。每两个神经元之间的连接代表加权值，称之为权重（weight）。不同的权重和激活函数，则会导致神经网络不同的输出。

图像经过平移，相应的特征图上的表达也是平移的。

卷积神经网络之层级结构

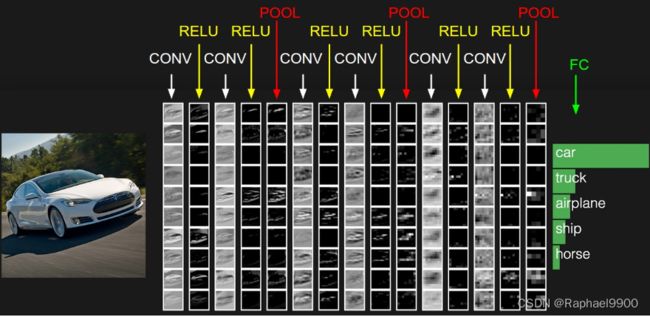
给定一张图片，是车还是马未知，是什么车也未知，现在需要模型判断这张图片里具体是一个什么东西，总之输出一个结果：如果是车 那是什么车。

 

• 最左边是数据输入层，对数据做一些处理，比如去均值（把输入数据各个维度都中心化为0，避免数据过多偏差，影响训练效果）、归一化（把所有的数据都归一到同样的范围）、PCA/白化等等。CNN只对训练集做“去均值”这一步。
• CONV：卷积计算层，线性乘积 求和。
• RELU：激励层，ReLU是激活函数的一种。
• POOL：池化层，即取区域平均或最大。
• FC：全连接层

池化

比如最大池化，它返回感受野中的最大值，如果最大值被移动了，但是仍然在这个感受野中，那么池化层也仍然会输出相同的最大值。

CNN并不是完全transition invariant

当目标小范围移动时，CNN才具有transition invariant，如果目标从左上角移动到了右下角，CNN没有平移不变性。关于平移不变性 ，对于CNN来说，如果移动一张图片中的物体，那应该是不太一样的。假设物体在图像的左上角，做卷积操作，采样都不会改变特征的位置，糟糕的是若把特征平滑后后接入了全连接层，而全连接层本身并不具备 平移不变性 的特征。但是 CNN 有一个采样层，假设某个物体移动了很小的范围，经过采样后，它的输出可能和没有移动的时候是一样的，这是 CNN 可以有小范围的平移不变性 的原因。

CNN 有不完全 transition invariant 无scaling invariant 无rotation invariant

CNN的机理使得CNN在处理图像时可以做到部分平移不变性（transition invariant），却没法做到尺度不变性（scaling invariant）和旋转不变性（rotation invariant）。即使是现在火热的transformer搭建的图像模型(swin transformer, vision transformer)，也没办法做到这两点。因为这些模型在处理时都会参考图像中物体的相对大小和位置方向。不同大小和不同方向的物体，对网络来说是不同的东西。这个问题在STL论文中统称为spatially invariant问题。

Spatial Transformer Layer STL 概览

 如图所示，如果是手写数字识别，图中只有一小块是数字，其他大部分地区都是黑色的，或者是小噪音。假如要识别，用Transformer Layer层来对图片数据进行旋转缩放，只取其中的一部分，放大之后然后经过CNN就能识别了。

STL 其实也是一个layer，放在了CNN前面，用来转换输入的图片数据，其实也可以转换feature map（一张特征图也可以看做一张图片），所以Transformer layer也可以放到CNN里面。

再说的直白一点，就是一个可以根据输入图片输出仿射变换参数的网络。

 上图是STN网络的一个结果示意图，(a) 是输入图片，(b) 是STN中的localisation网络检测到的物体区域，(c) 是STN对检测到的区域进行线性变换后输出，(d) 是有STN的分类网络的最终输出。

 

 STN的基本架构

 

主要的部分一共有三个，它们的功能和名称如下：

参数预测：Localisation net
坐标映射：Grid generator
像素的采集：Sampler

如上图，这个网络可以加入到CNN的任意位置，而且相应的计算量也很少。

将 spatial transformers 模块集成到 cnn 网络中，允许网络自动地学习如何进行 feature map 的转变，从而有助于降低网络训练中整体的代价。定位网络中输出的值，指明了如何对每个训练数据进行转化。

 

变换过程中，需要面对三个主要问题：

① 公式中参数应该怎么确定？
② 图片的像素点可以当成坐标，在平移过程中怎么实现原图片与平移后图片的坐标映射关系？
③ 参数调整过程中，权值一定不可能都是整数，那输出的坐标有可能是小数，但实际坐标都是整数的，如何实现小数与整数之间的连接？

如何实现参数选取？- Localisation net？

如果只是旋转、平移、缩放三种变换（都是 affine transformation），只需要确定6个参数。

线性变换从几何直观有三个要点：① 变换前是直线的，变换后依然是直线。② 直线比例保持不变。> ③ 变换前是原点的，变换后依然是原点。
仿射变换从几何直观只有两个要点（少了原点保持不变）：① 变换前是直线的，变换后依然是直线。② 直线比例保持不变。

 

 

 实现缩放

其实缩放也不难，如图所示，如果要把图放大来看，在x→(X2)→x′,y→(X2)→y′将其同时乘以2，就达到了放大的效果了。

缩小也是同样的原理，如果把这张图放到坐标轴来看，就是如图所示，加上偏执值0.5表示向右，向上同时移动0.5的距离，这就完成了缩小。

 

实现旋转
既然前面的平移和缩放都是通过权值来改的，那旋转其实也是。但是旋转应该用什么样的权值呢？

仔细思考，不难发现，旋转是跟角度有关系的，那什么跟角度有关系呢？- 正弦余弦

为什么正弦余弦能做旋转呢？

一个圆圈的角度是360度，可以通过控制水平和竖直两个方向，就能控制了，如图所示。

 

 可以简单的理解为 cosθ,sinθ 就是控制这样的方向的，把它当成权值参数，写成矩阵形式，就完成了旋转操作。

 实现剪切

剪切变换相当于将图片沿x和y两个方向拉伸，且x方向拉伸长度与y有关，y方向拉伸长度与x有关，用矩阵形式表示前切变换如下：

 由此，我们发现所有的这些操作，只需要六个参数[2X3]控制就可以了，所以我们可以把feature map U作为输入，过连续若干层计算（如卷积、FC等），回归出参数θ。

如何实现像素点坐标的对应关系？- Grid generator

如何表示采样前后像素点坐标对应关系？ - 仿射变换关系

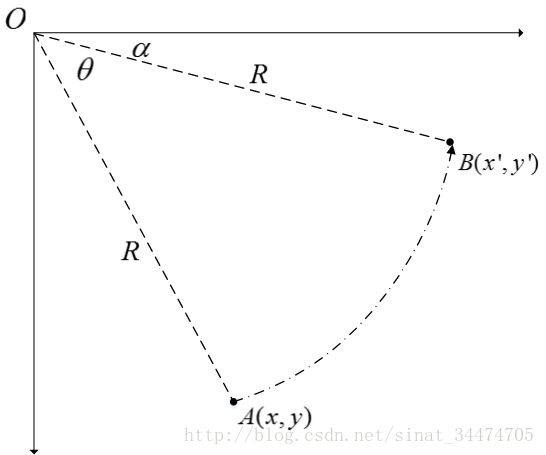
STL论文中定义了如图的一个坐标矩阵变换关系：

 

坐标映射关系是：

从目标图片（坐标固定）→原图片（坐标不固定）

让目标图片在原图片上采样，每次从原图片的不同坐标上采集像素到目标图片上，而且要把目标图片贴满，每次目标图片的坐标都要遍历一遍，是固定的，而采集的原图片的坐标是不固定的，因此用这样的映射。

 

如何解决小数坐标不可微？- Sampler 插值 Interpolation

为什么小数坐标不可微？- 微分为0无法梯度下降

Sampler 如何插值？

 图像分类任务

 

 2×ST−CNN表示在同一层是用了两个不同的STL，4 × ST − CNN 表示在同一层是用了四个不同的STL。图3-2右侧中的方框表示了不同STL要进行放射变换的位置。

可以看到不同的STL关注的鸟的部位也是不一样的，一个一直关注头部，一个一直关注身子。这就相当于是一个attention，把感兴趣的区域提取出来了。

还有一个地方是，这里的方框都是正的，这其实是因为作者把仿射变换中的参数[ b , c ]人为置0了，变成了

 李宏毅作业3

Augmentation Implementation增强实施

通过在代码中使用您所选择的图像大小来完成train_tfm来实现增强。复制你的train_tfm代码并粘贴到分级范围。

当多次给予相同的图像时，您的train_tfm必须能够产生5个+不同的结果。报告中的train_tfm可能与培训代码中的train_tfm不同。

Residual Connection Implementation剩余部分连接的实现

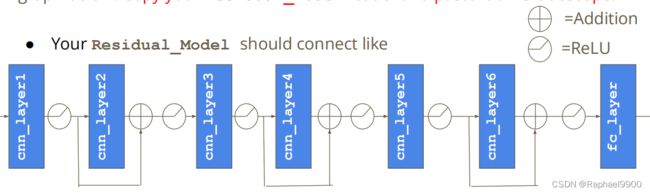
 残差连接被广泛应用于CNN，如图像识别的深度残差学习。残差值如下图所示。

 你的剩余模型应该连接像