小白科研笔记：点云目标检测相关文献速读-Part C
1. 前言
机器再跑网络，啥也干不了，接着看论文。之前的博客基本上把这两年SOTA的3D目标检测算法分析了一边。后续我会分析一些扩展的点云应用文章。
2. Attentional ShapeContextNet
首先看一篇CVPR2018的文章“Attentional ShapeContextNet for Point Cloud Recognition”。这是一篇使用点云注意力机制的文章。
2.1 Shape Context Kernel简介
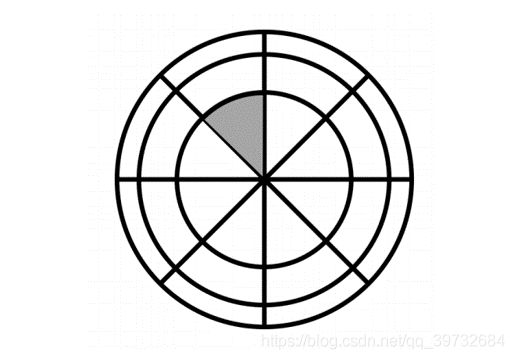
先看一个2D情况下的Shape Context Kernel（暂且译为离散形态核，可能不是很贴切）。在2D目标点做一个近邻2D球（圆），然后这个圆可以按角度和半径切，分成图1所示的若干部分。沿着半径切了三刀，即 n r = 3 n_r=3 nr=3。沿着圆周角切了八刀，即 n θ = 8 n_\theta=8 nθ=8。于是这个近邻2D球被分成 n r × n θ = 24 n_r\times n_\theta=24 nr×nθ=24个区间（英文描述是bin）。Shape Context Kernel由这24个子区间组成。进而可以得到关于这个目标点的24维数倍的描述子。这是传统2D描述子的套路。作者认为可以拓展到深度学习中。
图1：2D情况下的离散形态核
举例完2D情况，作者又讨论了3D情况。同样的道理，在3D目标点做一个近邻3D球，然后该球可以按水平角度，俯仰角度，以及半径切，分成若干部分。记水平角切分为 n θ n_\theta nθ个区间，俯仰角切分为 n ϕ n_\phi nϕ个区间，以及半径切分为 n r n_r nr个区间。于是这个近邻球被分成 L = n θ ∗ n ϕ ∗ n r L=n_\theta*n_\phi*n_r L=nθ∗nϕ∗nr个小区间。3D情况下目标点的Shape Context Kernel由这 L L L个子区间组成。这些都是经典计算机视觉中关于描述子的理论知识。虽说是经典，到现在还是有很多学者在深入研究并构建各式各样的描述中。把经典理论知识和深度学习网络结合，这样的研究思路，还是很有趣的。
2.2 Shape context block
在上一节，咱们说了3D情况下目标点的Shape Context Kernel可由 L L L个子区间组成。对于传统描述子理论，这 L L L个区间是有物理意义的，对应水平角俯仰角半径等。但是在深度学习中，在这篇文章里，作者把参数 L L L做了抽象，即3D情况下目标点的Shape Context Kernel可由 L L L个“区间”组成。“区域”是没有实际物理意义的。
作者的Shape context block分成Selection（关联构建），Aggregation（特征聚合），Transformation（特征抽取）三个部分。下面将介绍这三个部分。其实这三个部分也是泛图神经网络的主要组成部分。Shape context block简称为SC层。
A. Selection 关联构建
设点云有 N N N个点，即 p i ∈ R 3 p_i\in R^3 pi∈R3。然后对每一个"区间" l ∈ L l\in L l∈L，作者构建了一个关联矩阵（selection matrix） A l ∈ { 0 , 1 } N × N A^l \in \{0,1\}^{N \times N} Al∈{0,1}N×N。 A l ( i , j ) = 1 A^l(i,j)=1 Al(i,j)=1表示 p j ∈ b i n i ( l ) p_j\in bin_i(l) pj∈bini(l)，即第 j j j个点在第 i i i个点的第 l l l个“区间”上。 p j ∈ b i n i ( l ) p_j\in bin_i(l) pj∈bini(l)也可以等价为 p j − p i ∈ b i n ( l ) p_j - p_i \in bin(l) pj−pi∈bin(l)。作者用张量 A A A表示所有的关联矩阵，它是一个 N × N × L N\times N \times L N×N×L的张量。 A A A是需要深度学习学习出来的。而在传统计算机视觉中， A A A是人为定义的。
B. Aggregation 特征聚合
对于一个目标点 p i p_i pi，通过关联矩阵 A l A^l Al，可以了解到有一些点跟 p i p_i pi是相关的。作者希望把这些相关点的特征都聚合到一起。聚合的方式有平均，求和，和最大等等方式。聚合也可以看做是池化操作。作者使用的是求和聚合方式，聚合后的特征记为 m i m_i mi，它的计算方式如下所示。其中 p j ∗ p_j^* pj∗表示点 p j p_j pj对应的特征。
m i l = ∑ j A l ( i , j ) ⋅ p j ∗ m_i^l= \sum_{j} A^l(i,j)\cdot p_j^* mil=∑jAl(i,j)⋅pj∗
C. Transformation 特征抽取
Transformation的直译是变换，让人联想到坐标变换。但是在这篇文章中是特征抽取的意思。记函数 f ( ⋅ ) f(\cdot) f(⋅)表示Transformation Function，实际上它是一堆MLP。这是就是我把Transformation译为特征抽取的原因。目标点 p i p_i pi在SC层提取的特征记为 S C i SC_i SCi。它的计算方式如下所示：
S C i = f ( [ m i 1 , . . . , m i L ] ) SC_i = f([m_i^1,...,m_i^L]) SCi=f([mi1,...,miL])
2.3 SCNet
上一节讨论了SC层，事实上SCNet可由SC层嵌套组成。SC层就像一个带Attention机制的PointNet层一样。
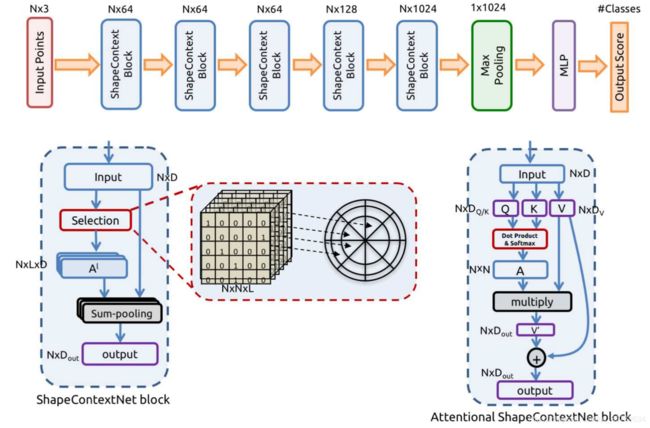
图2：SCNet示意图
2.4 Additional SC层
前面讨论了， A A A是一个 N × N × L N\times N \times L N×N×L的张量。对于大型雷达点云， N N N是几万甚至几十万更多，那么张量 A A A的存储是一个非常麻烦的事情，哪怕是使用稀疏张量存储。于是需要改进原有的SC层。作者做了些改进（感觉有点玄学，有效果就是好吧），如图2所示。这样一来， A A A是一个 N × N N\times N N×N的张量。不过还是有点大哈。
3. PCAN
这是篇CVPR2019的文章“PCAN: 3D Attention Map Learning Using Contextual Information for Point Cloud Based Retrieval”。这篇文章简洁明了，写的很好，值得学习。说实话，我喜欢这种简洁明了，丝毫不顾弄玄虚的文章。当然啦，文章还是要包装一下为好。首先看看作者的Attention机制：
图3：PCAN的示意图
Attention Map的计算过程图如下所示：
图4：Attention Map的计算过程
读了这篇文章，我就有一个感想，就是有意义的，提高性能的，可解释的，带有启发性的idea，要比一堆复杂的，不直观的，技巧（并不是说技巧都不重要），更能吸引人。
4. GAPNet
这是一篇2019年的文章“GAPNet: Graph Attention based Point Neural Network for Exploiting Local Feature of Point Cloud”。这篇文章的核心创新点是GAP Layer。GAP应该是Graph Attention based Point Neural Network的缩写。GAP Layer的计算示意图如下所示。它的Attention机制分为self-attention和neighboring-attention两部分。挺有启发性的。
图5：GAP Layer`的计算示意图
5. KPConv
这是篇ICCV2019的文章“KPConv: Flexible and Deformable Convolution for Point Clouds
”，核心创新点是Kernel Point Conv，即点核卷积。点核卷积的概念有些像CVPR2018的连续参数卷积，又有些像点云卷积PointConv。怎么说呢，基于点云的卷积彼此之间的差异并不是特别大。读文章的目的并不是简单地看到他们相似的地方，而是去发现它们独特的闪光点，如果那些文章有的话。2D点核卷积的示意图如下所示。这个图可以让一个入门者明白其思想。但是光凭这个图，很难看出它跟其他点云卷积之间的不同。
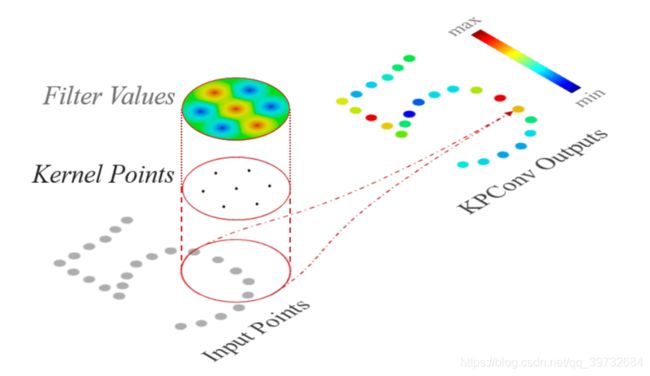
图6：2D点核卷积的示意图
仍然以2D卷积为例子，看一下点核卷积和2D普通卷积之间的不同之处，如图7所示。可见点核卷积适用于处理稀疏数据。点核卷积的感受野是以目标元素为中心的一个球域。在这个球域内构建核函数分布，然后以插值形式计算目标元素的卷积特征：
图7：点核卷积和2D普通卷积之间不同之处的示意图
作为论文的泛读，就看到这里。具体的计算过程的设计都是顺其自然的。值得一提的是，KPConv效果比SparseConv好。