用Python学《微积分B》(微分中值定理与洛必达法则)
本文将“微分中值定理”和“洛必达法则”(L'Hopital's Rule)两节的课后习题放到一块讨论。其中“微分中值定理”强调的是对概念,特别是“开区间可导,闭区间连续”的理解,习题虽少,但吃透不易;而“洛必达法则”将求函数的极限转变为求导数的极限,实现的是一种“降维”计算方法,(看到“降维”这个词,你就知道它的威力有多大了),但是现在有了python,这种苦逼计算就交给计算机了,至于它用不用“洛必达法则”,我就不关心了,我关心的是:“洛必达法则”在应用的时候如何对待求解不定式的分类和什么时候不适合用洛必达法则。
一、微分中值定理
本节包含了4个定理和4个推论,即:Fermat定理、Rolle定理、Lagrange中值定理、Cauchy中值定理,以及Lagrange中值定理的4个推论。
关于微分中值定理,最重要的是理解“开区间可导,闭区间连续”这一点。关于这点,知乎上有专门的讨论,链接是:https://www.zhihu.com/question/37423489
简单来说,闭区间可导就是耍流氓。举例证明:
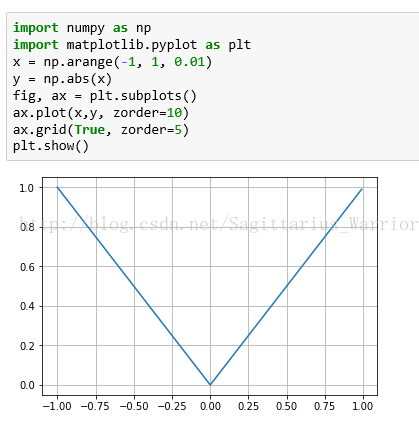
f(x) = |x|,在区间[-1, 0]和区间[0, 1]都可导,那么它在 x=0 这一点可导吗?
很显然:![]() ,它在 x = 0 不可导。如图:
,它在 x = 0 不可导。如图:
另一方面,函数连续反映的是函数在某点的极限与函数值的关系。闭区间连续与开区间连续是有本质区别的,不仅仅是两个端点的问题。这个在介绍“一致连续”的时候讲过了,闭区间连续,则一定“一致连续”。还是举例:
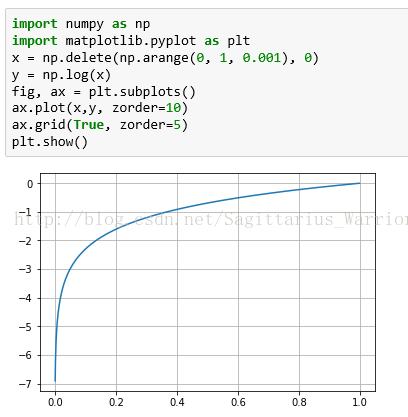
f(x) = ln(x)在 (0, 1)开区间连续
一般来说,没有特殊注明,“微分中值定理”就指的是“Lagrange中值定理”,但也不要忽视“Cauchy中值定理”的特殊作用。如果说,微分中值定理建立了“函数与导数”之间的联系,那么,“Cauchy中值定理”建立的就是“函数之比与导数之比”之间的联系,它在证明“Taylor公式的Lagrange余项”时就用到了。
1,如果函数f(x)和g(x)可导,那么以下说法中正确的是:
A. 若f(x)在区间[a, b]上单调增加,则f'(x) > 0 在[a, b]上恒成立
B. 若f'(x)在区间[a, b]上恒为0,则f(x) 在[a, b]上恒为常数
C. 若在区间[a, b]恒有f'(x)=g'(x),则 f(x)=g(x) 在[a, b]上恒成立
D. 若存在![]() 使得
使得![]() ,则存在(a, b)使得
,则存在(a, b)使得![]() ,且f(a)=f(b)
,且f(a)=f(b)
解:这一题几乎将Fermat定理和微分中值定理及其推论一网打尽。
A项实际上Lagrange中值定理的推论二的逆命题,那么这个逆命题对吗?看一个例题:
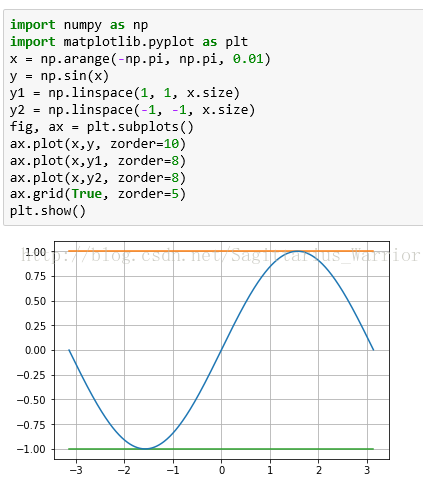
如上图 f(x) = sin(x) 在区间![]() 单调增加,但是它在两个端点的导数很明显等于0。
单调增加,但是它在两个端点的导数很明显等于0。
B项是Lagrange中值定理的推论一的逆命题,它成立。
C项比较简单,比如:f(x) = x + 2 与 g(x) = x + 4,导数相等,函数值不等。它要告诉我们的是:导数和函数值是两回事。
D项是Fermat定理的逆命题,即“导数为0的点一定是极值点”?举例:
如下图,很明显:f(0)不是极值点。
6,设函数f(x)在![]() 可导,C为常数,则以下结论正确的有几个:
可导,C为常数,则以下结论正确的有几个:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
解:
A项,考虑f(x) = sin(x) / x,(这就是sinc函数)。
很明显,f(x)趋向0,而f'(x)表示切线的斜率,它不存在。这个也可以从极限的定义或极限的保号性简单证明。这个选项告诉我们,极限与导数的差异,极限仅表征变化趋势,定性分析,可以是震荡的。
B项和C项,考虑f(x) = ln(x):
总结A和B两项,开区间(正无穷)端点上的函数和导函数之间没什么关系。
D项正确
8,设函数f(x) = arctan(x),
解:直接代入求解
二、洛必达法则
先看几个洛必达法则搞不定的例子:
前一个极限很明显,不适用洛必达法则。而后一个极限也不能用洛必达法则,因为,我们在求cos(x)的导数时,用到了待求的这个极限(它是两个特殊极限之一)。
很明显,它是0/0型,我们先用洛必达试试:
此时,看分子为1,分母振荡,极限不存在。那么是否这个极限真的不存在?
如果我们一开始用无穷小替换,会怎么样?
再仔细看洛必达法则的条件,其中一条就是“分子分母求导之后的表达式的极限要存在”。
所以,这个极限式分子分母求导之后的极限不存在,不适用洛必达法则。
这是一个无穷比无穷型的极限,先用洛必达法则试试:
同样地,此时极限不存在。
换个方法:
练习题:
1 - 4题:
第5题:
6-8题:
填空题:
附wiki链接:
Fermat定理指的是其中的“Fermat's theorem (stationary points)”,即“驻点”,极值。
https://en.wikipedia.org/wiki/Fermat%27s_theorem
https://en.wikipedia.org/wiki/Rolle%27s_theorem
Lagrange中值定理指的是其中的“mean value theorem”。
https://en.wikipedia.org/wiki/Lagrange%27s_theorem
https://en.wikipedia.org/wiki/Cauchy_theorem
https://en.wikipedia.org/wiki/L%27Hôpital%27s_rule