DynaVSR：使用元学习的动态自适应盲视频超分辨率方法

论文：DynaVSR: Dynamic Adaptive Blind Video Super-Resolution
代码：https://github.com/esw0116/DynaVSR

看点

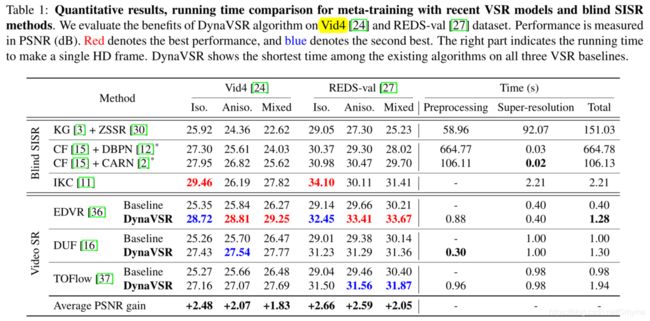
大多的监督超分算法都是通过使用固定的已知核函数对高分辨率数据进行降尺度得到低分辨率数据的，但这种方法在实际场景中并不成立。最近有人提出了一些盲超分算法去估计每个输入LR图像的不同降尺度核。然而它们的计算开销很大，不适合直接应用于视频。本文的贡献如下：

1. 提出了一个新的实时自适应框架DynaVSR，它通过元学习在测试时自适应的对未知的降尺度过程进行估计
2. 大大降低了估计实际降尺度过程的计算复杂度，从而能够在视频中实时超分
3. DynaVSR是通用的，可以应用于任何现有的VSR模型，以改进其性能
   

预知识：MAML

在深入研究本文的主要框架之前，简要地总结一下模型无关元学习（MAML）算法。元学习的目标是在很少的例子下快速适应新的任务。对于MAML，通过对参数进行一些梯度更新来模拟自适应过程。具体来说，MAML首先从当前任务$T_i\sim p(T)$中抽取一组示例$D_{T_i}$，其中$p(T)$表示任务的分布。然后，通过微调模型临时参数θ来适应当前任务：

$${\theta }_i^{\prime }=\theta \alpha {\nabla }_{\theta }{\mathcal{L}}_{{\mathcal{T}}_i}\left(S_{\theta }\left({\mathcal{D}}_{{\mathcal{T}}_i}\right)\right)\text{\hspace{1em}(1)}$$

其中，$L_{T_i}$是一个损失函数，$S_{\theta }$可以是任何参数化的模型。在适应每个任务$T_i$之后，从同一个任务中抽取新的示例$D_{T_i}^{{}^{\prime }}$来测试泛化能力并更新基本参数：
$$\theta \leftarrow \theta -\beta {\nabla }_{\theta }\sum _{{\mathcal{T}}_i}{\mathcal{L}}_{{\mathcal{T}}_i}\left(S_{{\theta }_i^{\prime }}\left({\mathcal{D}}_{{\mathcal{T}}_i}^{\prime }\right)\right)\text{\hspace{1em}(2)}$$

注意，等式(1)内循环更新，在训练和测试时都执行；而等式(2)外循环更新（元更新）只在训练期间执行。

方法

DynaVSR Overview

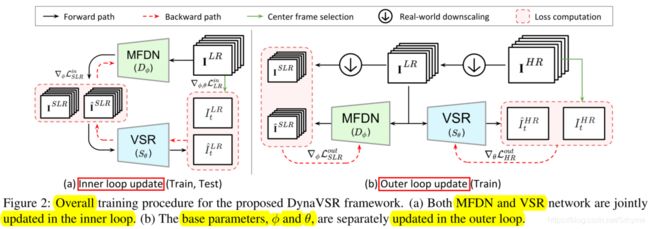
本文定义任务为超分辨每个输入视频序列。由于测试时只有输入LR帧可用，我们进一步缩小输入以形成超低分辨率（SLR）帧。然后，在给定SLR帧的情况下，通过预测LR帧来更新模型。在盲超分设置中，本文引入了一种高效的多帧降尺度网络（MFDN），并将其与VSR网络相结合。该框架能够很好地适应动态变化的视频输入，因此被命名为DynaVSR。下图展示了DynaVSR的整个训练过程，包括三个阶段：
1）用MFDN估计未知的降尺度过程
2）用每个输入视频对MFDN和VSR网络参数进行联合自适应，
3）对MFDN和VSR网络的基本参数进行元更新。在测试时，只对1）和2）进行处理，并使用更新后的VSR网络参数生成最终的超分辨率图像。

多帧降尺度网络

降尺度过程可以表示为：

$${\hat{I}}_t^{LR}=D_{\varphi }\left(I_t^{HR}\right)\text{\hspace{1em}(4)}$$

对于公式(4)中的$D_{\phi }$，本文提出了MFDN，它接收多帧LR输入并产生相应的进一步缩小的多帧输出。此过程为：

$${\hat{I}}_{t\in \mathbb{T}}^{SLR}=D_{\varphi }\left(I_{t\in \mathbb{T}}^{LR}\right)\text{\hspace{1em}(5)}$$

为了在保持效率的同时对不同的输入进行不同的核建模，我们用一个包含非线性的7层CNN对MFDN进行建模。为了处理多帧信息，MFDN的第一层和最后一层使用三维卷积，其余层使用二维卷积层。与现有方法相反，MFDN在测试时不需要额外的训练。这大大提高了估计未知降尺度过程的效率。
为了用单一的判别模型准确预测不同情况下的SLR帧，MFDN首先用不同的合成核进行预训练，然后应用到元学习框架中，进一步适应每个输入。训练LR-SLR对是由各向异性高斯核随机抽样产生的。注意，LR帧通过HR帧在合成核集中应用随机选择的核生成。然后由具有相同核的LR生成相应的SLR帧。通过最小化SLR和估计${\hat{I}}^{SLR}$之间的像素损失来进行MFDN的预训练。在预训练MFDN之后，在元训练过程中进一步微调MFDN，使其易于适应每个输入。虽然我们只使用合成核来训练MFDN，但它可以很好地推广到实际输入。

盲超分中的元学习

训练
对于内环更新，我们首先使用公式（5）生成${\hat{I}}_{t\in \mathbb{T}}^{SLR}$。然后将生成的SLR序列作为输入馈入VSR网络

$${\hat{I}}_t^{LR}=S_{\theta }\left({\hat{I}}_{t\in \mathbb{T}}^{SLR}\right)=S_{\theta }\left(D_{\varphi }\left(I_{t\in \mathbb{T}}^{LR}\right)\right)\text{\hspace{1em}(6)}$$

本文引入两个损失项来更新φ和θ：LR精度损失（$L_{LR}^{in}$）和SLR制导损失（$L_{SLR}^{in}$）。然而，$L_{LR}^{in}$本身不能保证更新后的MFDN能够产生正确的SLR帧。不准确的降尺度估计会产生错误的SLR帧，也会给VSR网络提供错误的更新信号。为了解决这一问题，我们提出了一种SLR制导损失来保证MFDN输出不会远离SLR的实际帧，内环更新的总损失计算如下：

$$\begin{array}{rl}{\mathcal{L}}^{in}& ={\mathcal{L}}_{LR}^{in}+{\mathcal{L}}_{SLR}^{in}\\ & =L_{VSR}\left({\hat{I}}_t^{LR},I_t^{LR}\right)+{\Vert {\hat{I}}_{t\in \mathbb{T}}^{SLR}-I_{t\in \mathbb{T}}^{SLR}\Vert }_1\end{array}\text{\hspace{1em}(7)}$$

上述过程对应为overview中的左半部分。对于外环，调整φ和θ的基本参数值（在内环更新之前），使模型更适应新的输入。给定输入LR序列，VSR网络和MFDN生成HR和SLR预测，相应如下：

$${\hat{I}}_t^{HR}=S_{{\theta }^{\prime }}\left(I_{t\in \mathbb{T}}^{LR}\right),{\hat{I}}_{t\in \mathbb{T}}^{SLR}=D_{{\varphi }^{\prime }}\left(I_{t\in \mathbb{T}}^{LR}\right)\text{\hspace{1em}(9)}$$

根据这两个预测，定义两个损失：

$$\begin{array}{rl}{\mathcal{L}}_{HR}^{out}& =L_{VSR}\left({\hat{I}}_t^{HR},I_t^{HR}\right)\\ {\mathcal{L}}_{SLR}^{out}& ={\Vert {\hat{I}}_{t\in \mathbb{T}}^{SLR}-I_{t\in \mathbb{T}}^{SLR}\Vert }_1\end{array}\text{\hspace{1em}(10)}$$

下图总结了DynaVSR训练的全过程。

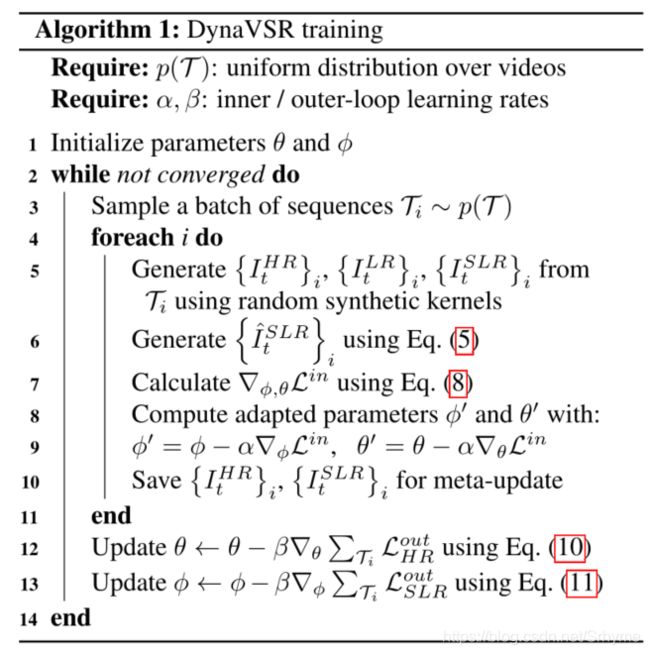
测试
在测试时，只执行内环更新以使MFDN和VSR网络参数适应测试输入帧序列。由于没有真实SLR帧，我们将其替换为预先训练的MFDN预测的SLR帧。虽然我们不使用真正的SLR帧，但我们在实验中表明，由MFDN生成的伪帧仍然有效。然后，可以使用更新的VSR网络生成最终输出HR帧。

实验

数据集

使用Vimeo90K进行训练。此外，还从YouTube收集了许多低分辨率视频，以演示DynaVSR在真实场景中的性能。

量化评估

对比不同降采样模型

在Vid4上各向同性高斯核上的定量结果

在Vid4上各向异性高斯核上的定量结果