手势识别Python-OpenCV

目录
一、选题背景 5
二、设计理念 5
2.1 搭建平台 5
2.2 问题描述 5
2.3 过程概述 6
三、过程论述 6
3.1 数据集生成 6
3.1.1 标准化图片的采集 6
3.1.2肤色检测 7
3.1.3 特征提取 8
3.1.3.1 手掌方向与掌心的寻找 9
3.1.3.2 第一特征——峰值个数 9
3.1.3.3 第二特征——夹角和 10
3.1.3.4 第三特征——距离平均值 11
3.1.3.5 第四特征——峰值距离和 12
3.1.3.6 其他特征 12
3.2 底层实现神经网络 12
3.2.1 使用神经网络的原因 12
3.2.2 神经网络算法简述与步骤 13
3.2.3 前向传播 14
3.2.4 反向传播与权重修改 15
3.2.5 神经网络算法交叉验证结果 16
3.3 底层实现KNN算法 17
3.3.1 选择KNN算法的原因 17
3.3.2 KNN算法思想与步骤 17
3.3.3 K值的选择 18
3.3.4 改进KNN算法 18
3.3.5 改进KNN算法交叉验证结果 21
3.4 SVM算法 21
3.4.1 选择SVM算法的原因 21
3.4.2 SVM算法原理简述 21
3.4.3 SVM算法实现 22
3.4.4 SVM算法交叉验证结果 23
3.5 SVM-KNN-神经网络组合模型 23
四、结果分析 24
五、算法应用 25
5.1 实时手势识别 25
5.1.1 手掌方向实时识别 26
5.2 动态手势识别 26
5.3 手势控制PPT 28
5.4猜拳小游戏 29
六、课程设计总结 30
6.1 课程设计的优点 30
6.2 遇到的问题与解决方案 30
6.3 课程设计心得 30
参考文献 31

基于SVM-KNN-神经网络组合模型的手势识别
一、选题背景
在当今智能化的时代，人工智能为人们的生活带来了许多的便利，模式识别作为人工智能领域的一门学科，就是一门用算法、用计算机来帮助人们识别各种类别的学科，人们的生产和生活日益依赖模式识别，如最常用的人脸识别、车牌识别等。然而手势也是人们日常生活中所用到较多的肢体语言之一，手势的识别能为生产生活产生巨大的作用，本文借鉴随机森林的思想——多个决策树投票产生结果，运用SVM算法、KNN算法、神经网络算法一同对手势进行识别，并利用识别算法进行简单的应用，如实时手势识别、动态手势识别、猜拳小游戏、手势控制ppt等，三种算法一同使用，具有较好的准确性与鲁棒性。
二、设计理念
2.1 搭建平台
本课程设计使用python编程语言，因为python语法简单而且是人工智能领域使用最多的编程语言，网络上已有大量的资料可以参考，在课程设计中遇到问题比较容易可以在网上得到相应的解答。但为了使用模式识别理论课所学知识，本课程设计避免使用现有的高度集成的库如tensorflow、keras等，从底层实现KNN算法与神经网络。
而编程环境使用vscode，因为本人之前一直有做前端，故对vscode的使用十分的熟悉，而且vscode小巧方便，有各种编程语言的插件与代码提示。
2.2 问题描述
本课程设计要解决的问题很简单，就是给定一张手势图片，能识别出是数字几，并能因此此算法进行实时手势识别，动态手势识别等应用。
开始动手之前有以下几个问题。
图片（数据集）从何而来？在网上找了一些比较出名的手势识别的数据库如11k Hands手部图像数据库、visual geometry group Hand Dataset数据库等，发现都不太理想，达不到期望的要求，因此，决定自制数据库。
如何进行识别？对图像进行特征提取后，使用SVM算法，KNN算法，神经网络算法分别对数据进行识别，最后把三种方法的结果进行投票表决。
如何进行应用？用三种算法合一的模型进行预测，使用opencv等库进行摄像头的调用与手势的提取，对实时图片进行识别即可。
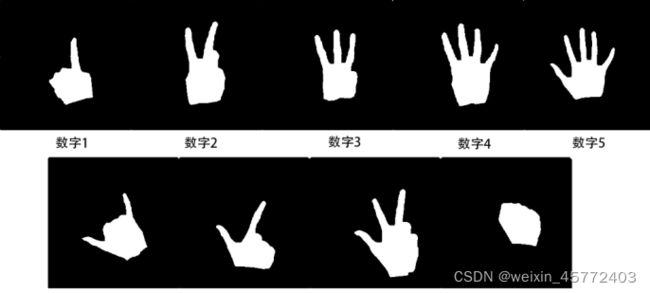图 2.2.1待识别的图片举例
2.3 过程概述
要想从零开始进行手势识别与应用，有着一系列的步骤，第一步，肯定是模式识别所需要的数据集的收集，使用自制的数据库的话就需要进行数据采集，采集到原始图片后要对图片进行处理，变成自定标准格式的图片，然后对图片进行特征的提取，删除不必要的特征，减少数据冗余度，拿到一堆有标签的数据后再分别实现KNN、SVM与神经网络算法的识别，三个模型的识别结果进行投票，形成三合一的模型，最后利用该模型进行实时静态手势识别、动态手势识别、猜拳小游戏与手势控制PPT。
整个流程方案如下：

图2.2.1 设计流程图
下面分别详细描述每个步骤的方法与过程。
三、过程论述
3.1 数据集生成
3.1.1 标准化图片的采集
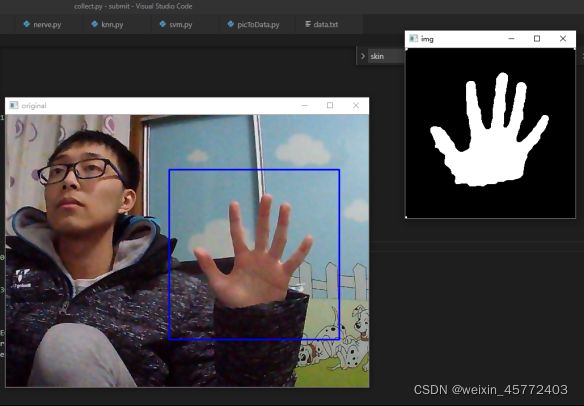
要采集手势图片，就必须调用摄像头进行采集等一系列操作，而如今在人工智能领域使用最多的图像处理的库就是opencv，有着许多方便的接口可以直接调用，因此，我们先使用opencv进行图像的处理：
（一）调用摄像头接口后规定手势识别的区域（300*300像素）
（二）对该区域内的图像进行双边滤波等图形学的处理，使手掌边缘平滑
（三）对该区域进行肤色检测并二值化，使手掌部分为白色，其他部分为黑色。
（四）对二值化后的图像进行滤波，平滑边缘。
（五）开运算，先腐蚀，让图片变“瘦”，再膨胀，让图片变“胖”，去除孤立的噪点。
（六）闭运算，先膨胀后腐蚀，去除内部噪点与小洞。
（七）最后就能得出标准化的图片，保存下来，用文件名表示类别即可，如1_2.jpg表示手势为数字一的第二张图片。

图3.1.1.1 标准化后的图像
3.1.2肤色检测
3.1.1的步骤中有最重要的一步，就是肤色检测。可以想到的最简单的方法就是对于皮肤的“肉色”进行识别，在规定范围颜色内的像素进行保留，不在此范围的像素进行剔除。
但对于肤色的检测往往会在一天不同时刻进行，图像的亮度变化会十分明显，平常图片使用RGB色域，对亮度比较敏感，进行检测的参数需要针对不同的亮度进行调节，因此，我们使用不受亮度影响的YCrCb即YUV色域，只检测Cr与Cb，排除亮度Y的影响。通过查询资料可知，亚洲人的皮肤范围在140≤Cr≤173，77≤Cb≤130之间，因此，只需要保留此范围内的像素即可。在opencv中可以直接使用inRange命令实现。

图 3.1.2.1 肤色检测代码

图 3.1.2.2 标准化图片提取过程

图 3.1.2.3 得到的图片集
一共采集了360张图片，9个手势，每个手势40张图片。
3.1.3 特征提取
得到标准化的图片后，我们为了精简数据集，我们就要进行特征的选择与提取，传统的做法也是将图片进行切割，有图像的地方为1，无图片的地方为0，最后变成一个只有0和1的矩阵，但我用另一种方式，既然是手势的识别，先找出手掌中心的点，然后将手掌边缘对于掌心的距离计算出来，一圈边缘下来，得到一组数据，绘制成图像，再最这组数据与图像进行分析与特征提取即可。
流程为：寻找轮廓→寻找掌心→计算轮廓到掌心的距离→特征寻找→特征提取
3.1.3.1 手掌方向与掌心的寻找
寻找轮廓可以直接调用opencv的findContours函数对图片进行所有轮廓的寻找，找出其中最大的轮廓即为手掌的轮廓。对于掌心的寻找，最简单的想法是直接计算所有轮廓的中心点，但是，由于手指的影响，轮廓的中心点会向手掌的的方向偏移，变得不是手掌中心点，如图3.1.3.1。

图 3.1.3.1 轮廓的中心点
掌心的定位错误会对后续的判断产生重大的影响，必须想办法修正。十分明显的想法是，把错误的定位往手掌的反方向进行移动一段距离即可，而手掌的方向如何确定，既然手指的影响会使轮廓中心向手掌反方向偏移，那么我们只需要将手指的影响加大，就能得到一个新的轮廓中心，而使用图形学的膨胀，就能使图像变胖，让手指向左右与向外进行扩展，比掌底膨胀得更多，增加手指的影响，再寻找轮廓中心。，用两个轮廓中心就能确定手掌的方向，也就能确定确定掌心了。
因此确定掌心的步骤为：
（一）对原图寻找轮廓，计算出轮廓的中心点
（二）对原图进行膨胀操作后再寻找轮廓，计算出新的轮廓中心点
（三）延长两点的连线到两点距离特定倍数的位置，即为掌心位置

图3.1.3.2两轮廓中心与修正后得到的掌心（左）膨胀后的图像（右）
3.1.3.2 第一特征——峰值个数
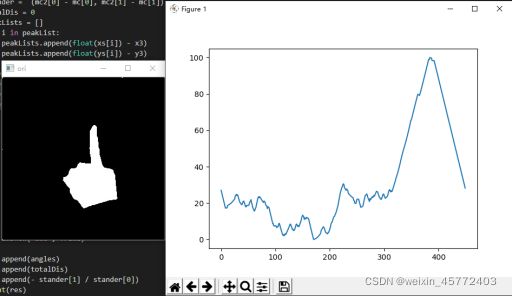
得到了掌心的位置，就可以计算所有轮廓到掌心的距离，并且进行归一化

绘制成图像。如图3.1.3.3 和图3.1.3.4分别为数字五和数字一的手势边缘对于掌心距离分布的图像，明显可以观察到，数字五的图像有5个峰值，数字一的图像有1个峰值，不难推断出，有几根手指伸出，得到的图像就有几个峰值，
判断峰值的方法为：先设定一个阈值，与图像的距离超过阈值并且比周围的60个点的数值都高，那么该点就为图像的峰值点。

图3.1.3.3 数字5手势边缘对于掌心距离分布的图像

图3.1.3.4 数字1手势边缘对于掌心距离分布的图像

由此，我们就得到了数据的第一个特征——峰值个数。
手势 1 2 3 4 5 6 7 8 0
峰值个数 1 2 3 4 5 2 2 3 不定
表 3.1.3.1 手势与峰值个数关系
3.1.3.3 第二特征——夹角和
由表3.1.3.1可以看出，不可能单纯通过峰值个数来判断手势，因此，我们要引入新的特征，我们已经知道了手掌的方向，那么，有相同个数峰值的手势如何区别，我们可以通过手指与手掌方向的夹角和进行判断。
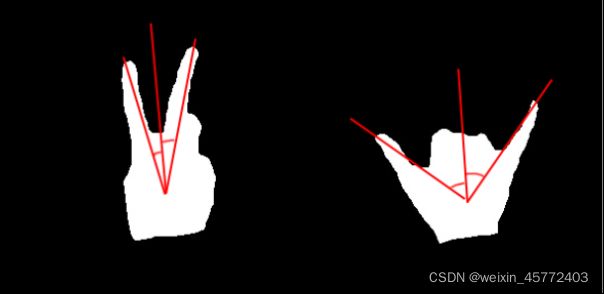
不同的手势，因为手指的位置不同，其与手掌方向的夹角和的大小的范围一般是不同的，感性分析，数字二与数字六的夹角对比，数字二夹角和偏小，数字六的夹角和偏大，由此我们就可以区分出具有相同峰值的手势。
夹角和的计算：我们已经得到了手掌方向与峰值的位置，而峰值的位置就是指尖的位置，运用高中数学，对所有指尖向量分别求其与手掌方向向量的夹角。

再用arccos求出角度，最后进行相加即可。

图3.1.3.5 数字二（左）与数字六（右）手指与手掌方向夹角
3.1.3.4 第三特征——距离平均值
通过峰值与夹角和我们已经可以判断出绝大部分的手势了，但是有一个特殊的手势——数字0的手势判断还不太好，虽然理论上数字0的峰值为0，但是实际的过程中，由于归一化的影响，会把边缘的噪点也响应放大，得到的峰值个数无法确定，而且采集得到的数字0也不是一个标准的圆，甚至可能出现为矩形的情况。因此，必须再寻找一个新的特征值。
通过感性分析，数字0的边缘到手掌中心的距离都比较接近，那么，进行归一化后，距离的平均值应该比其他图片的平均值要大，因此，在这里我们使用更能体现出大小差距的归一化公式

而不使用

将归一化后的所有距离求平均值，就得到了第三个特征——距离平均值，更好区分数字0与其他手势的同时，也能对其他手势的判别提高准确率

3.1.3.5 第四特征——峰值距离和
通过前三个特征其实已经基本可以实现手势的判别，但是为了进一步提高判断的准确率，我们引入第四个特征——峰值到掌心的距离的和，防止一些误判峰值的图像，增加识别的准确率。
3.1.3.6 其他特征
得到了上述四个特征后，我们可以开始运用算法进行模式识别了，但为了后续的应用部分，不需要再对图片进行读取，只对处理后的数据进行读取即可，我们再向数据中加入其他图像信息，但不用于识别算法的检测。
第一个数据就是手掌中心的位置，手掌位置的X与手掌位置的Y
第二个数据就为手掌方向，用手掌方向向量可以算出手掌方向的角度。
最后一个特征就是手掌大小占整张图片大小的比值，用于判断手掌离摄像头的远近。
到此为止，我们已经将一张手势的图片的特征基本提取完毕。提取出来的所有特征如下所示。

图3.1.3.6 提取出来的数据
只有虚线框住的数据用于模式识别。

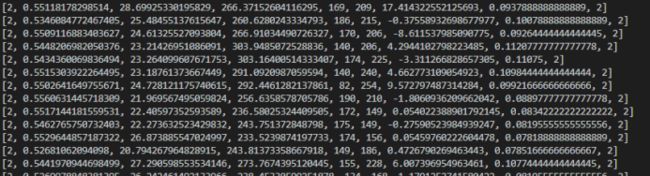
图3.1.3.7 生成的数据集（部分）
3.2 底层实现神经网络
3.2.1 使用神经网络的原因
得到了数据集后，就开始对数据进行训练，首先，我们先使用神经网络，因为神经网络作为当前人工智能领域使用最多的算法，其经过了工程与实际的检验，可靠性高，并且其几乎可以模拟所有函数，熟悉且运用神经网络的底层对于以后学习人工智能方面的知识有着极大的帮助，功能强大，使用率高，可靠，但是缺点是比较黑箱，对于不太满意的地方不能针对性调整，一般只能调整训练集，并且训练时运算量大，耗时可能会久，但其训练好模型后前向传播的速度极快，应用时的计算量不算太大。因此，选择使用神经网络算法。
3.2.2 神经网络算法简述与步骤
神经网络本质上就是一个个神经元的组合，每个神经元，对于所有输入，先乘上一个对应的权重值w，再求和后加上该神经元的偏置，最后输入到激活函数中，激活函数的输出形成该神经元的输出，通常，取激活函数为Sigmoid函数。
则一个神经元的输出为：

图3.2.2.1 神经元简图
而将多个神经元一层层组合在一起，就可以形成神经网络，每一个神经网络的输入是前一个层的所有神经元的输出，而该神经元的输出又作为下一层神经元的输入，最后得到最终的输出。

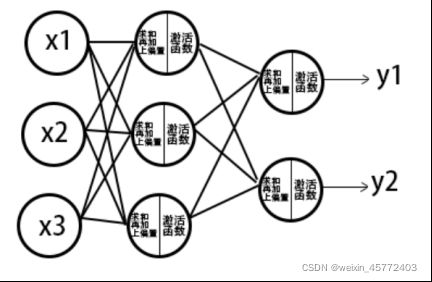
图 3.2.2.2 一种三输入二输出的神经网络结构
如上图，是一种三输入二输出的神经网络结构，有三层结构，一层输入层，一层隐藏层，一层输出层，对于每个神经元都遵循着规定的计算方式，最终既能得出结果。
因为我们的数据有4个特征，9种手势，因此，我们定义一个层数为4、80、180、9的神经网络结构，输入为4个特征，训练标签为one-hot标签，既[y1,y2…]中只有对应一个值为1，其余值为0
而运用神经网络进行模式识别，其最基本的就为前向传播与反向传播，其基本步骤如下：

图 3.2.2.1 神经网络算法步骤
下面来详细介绍每一步的过程。
3.2.3 前向传播
神经网络的工作过程就是前向传播的过程，但由于神经网络一般使用大量的数据，而寻常的神经网络公式是处理单个输入的，而数据量大时一般使用矩阵进行计算，因为矩阵的乘法有优化算法，能比单纯的一个个乘速度更快，并且用矩阵表示数据时公式更为简单方便。由一个神经元的输入与输出公式可以推导出，一层神经元的输入输出关系为：

假设上一层有n个神经元，当前层有m个神经元，故公式中为上一层神经元的输出，其格式为[x1, x2, x3 …]，为1*n的矩阵。为当前层的权重值，其格式为：

为上一层第n个神经元对当前层第m个神经元的权重。
为当前层的偏置，其格式为[b1, b2, b3 …]，为1*m的矩阵
为激活函数，此处我们选择Sigmoid函数
计算出当前层的输出后，继续计算下一层的输出，直到计算到输出层，得到神经网络输出，既完成前向传播的过程。

图 3.2.3.1 前向传播的函数代码
3.2.4 反向传播与权重修改
反向传播实际上损失函数对每个权重求偏导的过程。手写底层神经网络的话我们使用最基本的平方损失函数

计算神经网络预测输出与数据标签的差值即可得到数据的损失值。使用求导的链式法则我们就可以得到损失函数对每个权重的偏导，用矩阵形式表示为：

图 3.2.4.1 反向传播四公式
对于上述四个公式，为损失函数对每一层的权重的敏感值，后两个公式则分别为损失函数对每一层偏置与权重的偏导数，由于我们使用的激活函数为Sigmoid函数。

其导数为：
而损失函数的导数为

因此，改写前两个公式为：

得到损失函数对每个权重与偏置的偏导后，利用梯度下降的思想，用

其中lr为学习率，就能更新每个权重的值，用python进行数学公式的实现，就是实现反向传播的过程，以下为代码实现。

图 3.2.4.2 反向传播代码
3.2.5 神经网络算法交叉验证结果
使用10倍交叉验证来进行模型的验证，所谓交叉验证，就是在数据集中临时挑选一部分数据作为训练集，剩下作为测试集，得到一个错误率，然后又抽另一部分作为训练集，剩下作为测试集，又得到一个错误率，如此往复，将得到的错误率求平均值，既为交叉验证的错误率。而10倍交叉验证就是将数据分成10份，每次拿9份作为训练集，一份作为测试集，在测试集不重复的情况下可重复10次，得到10个错误率，取平均值，既可得到近似所有样本用来训练的错误率。
进行10倍交叉验证，首先先对数据进行整理，整理出10个带训练的测试集与数据集，由于手势识别一共有9个类，为了保证训练与测试的鲁棒性，训练集与测试集中都必须有每个类，因此，不能对整个数据集进行随机抽样，要进行分层抽样，最后再合并在一起，形成10组训练与测试集。

图 3.2.5.1 交叉验证代码

图 3.2.4.2 神经网络交叉验证错误率

可以得出，对神经网络进行10倍交叉验证得到的错误率为：
测试集中的错误率为：2.7%
训练集中的错误率为：3.05%

3.3 底层实现KNN算法
3.3.1 选择KNN算法的原因
KNN算法既k近邻法，只要判断其最近的K个样本的类别，找出最多类别的类即可。算法虽然简单，但是可靠，不怕异常数据，也无需过多地调节参数，只需要判断K的值多大即可，其可靠程度可以增加模型的稳定性。
3.3.2 KNN算法思想与步骤
k近邻法的思想为：设N个已知样本分属于c个类，i=1,…c，考察样本中的前k个近邻，设其中有个属于类，则类的判别函数为：

决策规则为：若
基本步骤为：
（一）对数据进行归一化，防止较大值的维度影响大，而值小的维度影响小
（二）求出x与所有样本距离
（三）找出与x距离最近的k个样本的值
（四）统计这k个样本的所属的类，看所属哪个类最多
（五）判别样本为最多所属的那个类

图 3.3.2.1 原始knn算法代码实现
3.3.3 K值的选择
K近邻法中k值过小会影响分类精度，而k值过大会造成误差，包含噪音，因此，必须选择一个合适的k值，使用遍历法，对k取1-15，观察其训练出来测试集的准确率，选取准确率最大的k值。

图 3.3.3.1 不同k值中测试集的准确率
从结果可以看到，应该选K=3或K=1，但为了增加鲁棒性，去K=3
3.3.4 改进KNN算法
对于原始的KNN算法，其原理十分简单，但是需要在样本数量较多的情况下才能有较好的结果，但是样本数量一多，那么在算法的第二步——求与所有样本的距离时，所需要的运算量就十分大，所需要的时间会比较久，特别是在交叉验证时，需要同时对训练集与测试集进行10轮识别，其所需要的时间过多（本人亲测），因此，考虑对算法进行改进。
既然想要在最短的时间内找到最近的k个数，那么，从一维出发，实际上就数据搜索算法，比较著名的数据搜索算法有二叉树算法。

图 3.3.4.1 二叉树算法
二叉树的性质为
（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值
（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值
（3）左、右子树也分别为二叉排序树
而用二叉树进行一维数据的搜索，只需要从根结点出发，往叶结点方向寻找，就能很快找到最近的结点，有许多数据是不需要计算的，大大减少了计算量，提高算法的速度。
而我们的想法就是构建一个多维的二叉树来进行数据的查找，提高KNN算法的速度，也就是使用Kd树进行数据查找。
模拟二叉树，Kd树的性质为
（1）若左子树不空，则左子树上所有结点对应分割维度上的值小于根结点分割维度上的值
（2）若右子树不空，则右子树上所有结点对应分割维度上的值小于根结点分割维度上的值
（3）左、右子树也分别为Kd树

图 3.3.3.2 二维kd树
因此，可以得出用样本数据构建kd树的过程：取分割维度为k（k=深度%4）,将样本以分割维度进行排序，取中位数的值，比中位数上分割维度值小的为左节点构建kd树，并深度加1，大的为右结点构建kd树,深度也加一。如此迭代下去，就能构建出Kd树。

图 3.3.3.3 构建kd树代码
使用kd树进行K近邻法的搜索，步骤为：
1、先给定最近的K个点，与样本点距离均为无穷
2、先从根结点出发，当前结点为根结点
3、计算已有最近K个点中最大的距离是否大于与样本与当前结点的距离，若是，则用当前结点替换，作为最近的K个点之一
4、判定样本点与当前结点在分割维度上的值的大小，大于或等于当前结点的话，就对右结点进行搜索，既对右结点从步骤3开始搜索，小于当前结点则既对左结点从步骤3开始搜索，直到叶结点。
5、从叶结点进行回溯，判断样本值与当前结点分割超平面的距离和K个最小样本中的最大距离的大小，如果大于最小值，则该分支停止搜索，如果小于，则需要去到当前结点的右结点上进行3-5步骤。
6、得到最近的K个点。

图 3.3.3.4 kd树搜索代码
得到最近的K个点后，使用传统的KNN算法进行计算即可。
3.3.5 改进KNN算法交叉验证结果
对改进后的KNN算法进行10倍交叉验证，虽然理论上与改进前的KNN算法的结果一样，但是运算速度快，更有利于实时手势识别。
经过10倍交叉验证后，得到KNN算法的结果如下：

图 3.3.4.1 KNN算法交叉验证错误率
可以得出，对KNN进行10倍交叉验证得到的错误率为：
测试集中的错误率为：2.7%
训练集中的错误率为：1.6%

3.4 SVM算法
3.4.1 选择SVM算法的原因
由于数据集为自己采集的数据量很小，而从很小的数据得到比较准确的值，这恰好就是SVM算法的优点，能通过小样本得到高准确率，因为只有小部分的样本作为支持向量。因此，选择SVM算法。
3.4.2 SVM算法原理简述
SVM算法，实际上就是用两个最大间隔的超平面将各类分开，最大间隔超平面是位于它们正中间。两个超平面的的函数为：
与
而最大间隔平面的函数为：

由数学可以证明出，任意一点到最大间隔平面的距离为，而在两分割面上的点满足,因此，两分隔面的距离为M =

图 3.4.2.1 svm分隔面与最大间隔超平面

要想得到最大间隔的分割面，实际上就是最大化，可以转化为最小化
约束条件为：

而使用KKT条件与拉格朗日乘子就能够解出此凸优化问题。
3.4.3 SVM算法实现
由于对KKT条件与拉格朗日乘数法所需要的数学知识不太熟悉，因此，使用sklearn的提供的SVM接口来进行SVM算法的调用,进行10轮的交叉验证，并选取测试集准确率最大的SVM模型进行保存，便于后续使用

图 3.4.3.1 SVM算法代码实现

3.4.4 SVM算法交叉验证结果
对于SVM进行10倍交叉验证，得到的结果如下

图 3.4.4.1 svm交叉验证错误率

可以得出，对SVM进行10倍交叉验证得到的错误率为：
测试集中的错误率为：1.2%
训练集中的错误率为：2.5%
3.5 SVM-KNN-神经网络组合模型
为了提高模型的鲁棒性与准确性，试图将三种算法集合成一种算法，模拟随机森林的思想，将SVM、KNN、神经网络的各自的预测结果进行投票，再得出最终的结果。

图 3.5.1 SVM-KNN-神经网络组合模型

因此，只需要将上面已经单独实现好的功能进行整合，形成一个新的算法即可，而且SVM与神经网络的前向传播算法的运行速度很快，相对于使用Kd树进行优化后的KNN算法来说时间也可以忽略不计，因此在也不会增加很多时间的成本，具有一定的可行性。

图 3.5.2 SVM-KNN-神经网络组合模型代码实现

四、结果分析
也如同SVM、KNN、神经网络单独使用时一样，对SVM-KNN-神经网络组合模型使用10倍交叉验证。

图 3.4.4.1 SVM-KNN-神经网络组合模型交叉验证错误率
可以得出，对SVM-KNN-神经网络组合模型进行10倍交叉验证得到的错误率为：
测试集中的错误率为：0.74%
训练集中的错误率为：1.6%
整合总共四种算法的错误率如下：

表4.1 四种算法10倍交叉验证错误率对比
10倍交叉验证 测试集（%） 训练集（%）
神经网络 2.7 3.05
KNN 2.7 1.6
SVM 1.2 2.5
SVM-KNN-神经网络组合 0.74 1.6
由上表可见，使用SVM-KNN-神经网络组合模型比单独使用3种算法时的准确率更高，错误率更低，效果更好。
五、算法应用
5.1 实时手势识别
既然已经能够对处理好后的数据进行识别与分类，而且从图像采集到数据处理的过程都是亲手完成的，那么，只要将之前图像采集、数据处理、算法实现的代码进行整合，完全可以进行实时的手势识别，并且在图像处理的过程中，还有一些没有被模式识别应用的特征，如掌心位置，手掌方向与手掌占比等，充分利用这些特征可以做出更多的应用实例。

图 5.1.1 实时手势识别的应用

图 5.1.2 九种手势的实时手势识别
5.1.1 手掌方向实时识别
利用图像处理处理后得到的手掌方向，可以进行手掌方向的识别。

图 5.1.1.1数字一手势的手掌方向示例

图 5.1.1.2 数字一各种方向的识别
5.2 动态手势识别
图像处理后的数据还有着掌心位置与掌心占比的信息，利用多张图片的掌心位置，就可以进行动态的手势识别，方法如下。
（一）储存一段时间的处理后的数据与识别结果，形成一个二维数组
（二）判断该数组中是否有连续10次以上识别出某个相同的手势，如果有，则进入下一步
（三）提取该连续手势的数组，判断其掌心x与掌心y的极差，如果超过某个阈值，则证明有移动，移动不超过，这证明不移动。
（四）有移动时，提取出连续手势的掌心x与掌心y，使用最小二法公式

可以算出x与y的斜率，利用斜率求出角度，既为手掌运动轨迹所在直线方向
（五）再通过对x与y的变化趋势判断，判断其增大趋势还是减小趋势，就能确定手掌的移动方向

图 5.2.1 某次动态手势识别的x与y数据最小二乘法应用

由上述算法就可以算出手掌移动的方向，是向右滑、向左滑、向上滑、向下滑、向右上滑、向左上滑、向右下滑、向左下滑。

图 5.2.2 判断手掌移动方向代码

图 5.2.2 动态手势识别示例
采用同样的方式，对手掌占比进行阈值与趋势判断，就能判断出手掌在“变大”还是在“变小”，实现推和拉两种动态手势。
5.3 手势控制PPT
既然已经实现了动态手势识别，那么就可以像华为手机的手势操控一样，利用手势来进行控制，我们选择控制PPT，使用python的pyautogui库进行鼠标与键盘的控制，检测到相应的手势就进行相应的动作。我们定义：
表5.3.1 控制PPT手势表
手势 PPT控制 鼠标键盘操作
向右滑 PPT下一页 键盘按方向键右
向左滑 PPT上一页 键盘按方向键左
推 PPT放大 滚轮向前
拉 PPT缩小 滚轮向后

图 5.3.1 手势控制PPT示例
5.4猜拳小游戏
既然已经可以实时识别出一个了0-8九种手势，而剪刀石头布游戏中的剪刀对应数字2，石头对应数字0，布对应数字5，再增加一个识别区域，同时对两个区域的手势进行识别，再根据判断出来的手势进行胜负的判断，就能够实现猜拳小游戏。

图 5.4.1 猜拳小游戏示例

图 5.4.2 判断猜拳输赢手势代码
六、课程设计总结
6.1 课程设计的优点
花费了接近一个星期的时间在手势识别的课程设计上，期间学到了许多东西，不断完善自己的课程设计，增加功能，力求完美，因此，该课程设计有以下优点。
（一）使用三种算法SVM-KNN-神经网络组合模型进行模式识别,比使用单一的算法的准确率更高，鲁棒性更强。
（二）工作量大，功能多。从数据集的采集，到特征选择和提取，再分别实现三种算法，再利用算法进行实际的实时手势识别、动态手势识别、猜拳小游戏、手势控制PPT等应用，单是应用的文件就有超过千行代码。
（三）基于底层，少用库。KNN与神经网络算法完全是基于底层算法原理编写的，只用到了纯粹的矩阵运算，能比较直观的感受算法的基本原理
（四）代码规范。本人一直注重代码规范，并且由于之前一直写前端，遵循着eslint代码规范要求，使用小驼峰命名法，函数功能都有注释。
6.2 遇到的问题与解决方案
在课程设计的过程中，免不了出现各种各样的问题，但最后都能通过上网找资料进行解决或使用某种方式绕开，一下为一下遇到的问题。
（一）设备问题。笔记本的摄像头色差大，分辨率低，后来通过淘宝买了一个摄像头，没想到买回来的摄像头自带美颜功能且无法关闭，导致在使用过程中对于静止不动的画面，摄像头拍出的图片也有明显的变化，导致原来是用opencv的背景减除法createBackgroundSubtractorMOG2进行手势的提取，由于摄像头的噪音过大，而改用YcrCb色域法。
（二）局部最低点问题。在进行神经网络识别时，由于是手写底层，只使用了简单的梯度下降法进行训练，因此，不仅需要迭代的次数多，并且也会陷入局部最低点，最后，该问题通过改变神经网络权重初值解决。
（三）KNN算法运算速度慢问题。一开始使用的是传统的K近邻法，所需要的运算量较大，并且在10轮交叉验证中分别对测试集与训练集进行错误率判断，让我一度以为自己的电脑卡死了，最后使用优化的KNN算法，构建Kd树来解决。
（四）中文乱码问题。不论是opencv还是pyplot，在要显示中文时都会出现乱码问题，对于opencv，只能通过将图片转换成另一个图像处理库PIL的格式，在PIL上处理好文字的显示，再转换回去，而值pyplot上，就能使用unicode编码解决。
6.3 课程设计心得
经过接近一个星期的课程设计，虽然遇到了许多问题，但也学到了许多东西，体会到了神经网络的底层的如何一步步反向传播的，见识到了简简单单的k近邻法的威力，也看到了SVM强大的分隔能力，在一系列数据采集、数据处理、特征提取、算法实现、算法应用的过程中，真切体会到了如何实现一个简单识别算法的过程。有着识别失败的失望，也有着识别准确率提高的高兴，更是利用所写的算法进行猜拳小游戏与控制PPT等实用功能，体会到了科技如何服务于生产。同时，也在实现算法的过程中发现自己理论知识的不足，理解了知识与理论的重要性，加深了对模式识别理论知识的理解，让我受益匪浅。

参考文献
[1]张辉,邓继周,周经纬, 等.基于几何特征的桌面静态手势识别[J].计算机工程与设计,2020,41(10):2977-2981. DOI:10.16208/j.issn1000-7024.2020.10.045.
[2]赵旖旎.基于视觉的静态手势识别技术研究[D].湖北:华中科技大学,2019.

附录
由于代码过多并且提交的为电子版文件，附录就不展示所有的代码，只展示SVM-KNN-神经网络组合模型的手势识别的算法，所有程序均在同目录下的文件夹中，有Readme文档说明每个文件的功能。

SVM-KNN-神经网络组合模型（total.py）
import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm
import random
from sklearn.model_selection import KFold
import matplotlib.pyplot as plt

加载单个数据集

def loadData(rate):
data = np.load(‘data.npy’).tolist()
datas = []
for i in range(9):
datas.append([])
for item in data:
if int(item[8]) == 11:
# print(‘con’)
continue
# print(int(item[7] - 1))
datas[int(item[7] - 1)].append(item)

trainData = []
testData = []
for item in datas:
    number = int(rate * len(item))
    choise = random.sample(range(len(item)),number)
    for i in range(len(item)):
        if i in choise:
            testData.append(item[i])
        else:
            trainData.append(item[i])

trainData = np.array(trainData)
testData = np.array(testData)
trainX = trainData[:,0:4]
trainY = trainData[:,-1]
testX = testData[:,0:4]
testY = testData[:,-1]
return trainX, trainY, testX, testY

n倍交叉验证法辅助函数，对于一个数组提取测试集与验证集

def CrossVDataSplit(datas, n):
datas = np.array(datas)
kf = KFold(n_splits=n,shuffle=True)
trainData = []
testData = []
for train_index, test_index in kf.split(datas):
TtrainData = datas[train_index]
TtestData = datas[test_index]
trainData.append(TtrainData.tolist())
testData.append(TtestData.tolist())
return trainData, testData

n倍交叉验证法数据生成

def CrossVData(n):
data = np.load(‘data.npy’).tolist()
datas = []
for i in range(9):
datas.append([])
for item in data:
datas[int(item[8] - 1)].append(item)
datas = np.array(datas)
trainData = []
testData = []
for item in datas:
item = np.array(item)
trainD, testD = CrossVDataSplit(item, n)
trainData.append(trainD)
testData.append(testD)
trainDatas = []
testDatas = []
# print(np.array(trainData[0][0]).shape)

for i in range(n):
    tempTrain = np.empty((0,9))
    tempTest = np.empty((0,9))
    for j in range(9):
        tempTrain = np.vstack((tempTrain, np.array(trainData[j][i])))
        tempTest = np.vstack((tempTest, np.array(testData[j][i])))
    trainDatas.append(tempTrain)
    testDatas.append(tempTest)
return trainDatas,testDatas

kd树

class kd_tree:
def init(self, value):
self.value = value
self.dimension = None
self.left = None
self.right = None

def setValue(self, value):
self.value = value

kd数搜索，减少搜索时间

def creat_kdTree(dataIn, k, root, deep):
if(dataIn.shape[0]>0):
dataIn = dataIn[dataIn[:,int(deep%k)].argsort()]
data1 = None; data2 = None

if(dataIn.shape[0]%2 == 0): 
  mid = int(dataIn.shape[0]/2)
  root = kd_tree(dataIn[mid,:])
  root.dimension = deep%k
  dataIn = np.delete(dataIn,mid, axis = 0)
  data1,data2 = np.split(dataIn,[mid], axis=0) 

elif(dataIn.shape[0]%2 == 1):
  mid = int((dataIn.shape[0]+1)/2 - 1) 
  root = kd_tree(dataIn[mid,:])
  root.dimension = deep%k
  dataIn = np.delete(dataIn,mid, axis = 0)
  data1,data2 = np.split(dataIn,[mid], axis=0)
deep+=1
root.left = creat_kdTree(data1, k, None, deep)
root.right = creat_kdTree(data2, k, None, deep)

return root

#k近邻搜索
def findKNode(kdNode, closestPoints, x, k):
if kdNode == None:
return
curDis = (sum((kdNode.value[0:4]-x[0:4])**2))**0.5
tempPoints = closestPoints[closestPoints[:,9].argsort()]
for i in range(k):
closestPoints[i] = tempPoints[i]
if closestPoints[k-1][9] >=1000000 or closestPoints[k-1][9] > curDis:
closestPoints[k-1][9] = curDis
closestPoints[k-1,0:9] = kdNode.value
if kdNode.value[kdNode.dimension] >= x[kdNode.dimension]:
findKNode(kdNode.left, closestPoints, x, k)
else:
findKNode(kdNode.right, closestPoints, x, k)
rang = abs(x[kdNode.dimension] - kdNode.value[kdNode.dimension])
if rang > closestPoints[k-1][9]:
return
if kdNode.value[kdNode.dimension] >= x[kdNode.dimension]:
findKNode(kdNode.right, closestPoints, x, k)
else:
findKNode(kdNode.left, closestPoints, x, k)

knn中判断哪个类最多

def findMaxIndex(closePoint):
t = [0 for i in range(9)]
for item in closePoint:
# print(item)
t[int(item[-2]) - 1] += 1
mIndex = 0
for i in range(9):
if t[mIndex] < t[i]:
mIndex = i
return mIndex + 1

标签one-hot处理

def onehot(targets, num):
result = np.zeros((num, 9))
for i in range(num):
result[i][int(targets[i]) - 1] = 1
return result

逆向one-hot

def reverOneHot(arr):
for i in range(len(arr)):
if arr[i] == 1:
return i + 1
return i

sigmoid

def sigmoid(x):
return 1 / (1 + np.exp(-x))

sigmoid的一阶导数

def Dsigmoid(x):
return sigmoid(x)*(1-sigmoid(x))

#神经网络模型
class Modle(object):

#初始化
def __init__(self, l0 = 10, l1 = 10, l2 = 10, l3 = 10):
    # self.lr = 0.001            # 学习率
    self.lr = 1e-6
    self.W1 = np.random.randn(l0, l1) * 0.1    
    self.b1 = np.random.randn(l1) * 0.1
    self.W2 = np.random.randn(l1, l2) * 0.1
    self.b2 = np.random.randn(l2) * 0.1
    self.W3 = np.random.randn(l2, l3) * 0.1
    self.b3 = np.random.randn(l3) * 0.1

def setW(self, w1, b1, w2, b2, w3, b3):
    self.W1 = w1
    self.b1 = b1
    self.W2 = w2
    self.b2 = b2
    self.W3 = w3
    self.b3 = b3

# 前向传播
def forward(self, X, y):
    self.X = X                                     
    self.z1 = np.dot(X, self.W1) + self.b1           
    self.a1 = sigmoid(self.z1)

    self.z2 = np.dot(self.a1, self.W2) + self.b2       
    self.a2 = sigmoid(self.z2)

    self.z3 = np.dot(self.a2, self.W3) + self.b3      
    self.a3 = sigmoid(self.z3)

    loss = np.sum((self.a3 - y) * (self.a3 - y)) / 2  
    self.d3 = (self.a3 - y) * Dsigmoid(self.z3)       
    return loss, self.a3

# 预测，实际上就是前向传播再成one-hot形式
def predict(self, X):
    self.X = X                                 
    self.z1 = np.dot(X, self.W1) + self.b1      
    self.a1 = sigmoid(self.z1)

    self.z2 = np.dot(self.a1, self.W2) + self.b2  
    self.a2 = sigmoid(self.z2)

    self.z3 = np.dot(self.a2, self.W3) + self.b3        
    self.a3 = sigmoid(self.z3)
    a3 = self.a3

    for i in range(a3.shape[0]):
        mIndex = 0
        for j in range(a3.shape[1]):
            if j == mIndex:
                continue
            if a3[i,j] > a3[i,mIndex]:
                a3[i,mIndex] = 0
                mIndex = j
            else:
                a3[i,j] = 0
        a3[i,mIndex] = 1

    return a3

#反向传播
def backward(self):
    dW3 = np.dot(self.a2.T, self.d3)                 
    db3 = np.sum(self.d3, axis=0)                  

    d2 = np.dot(self.d3, self.W3.T) * Dsigmoid(self.z2)  
    dW2 = np.dot(self.a1.T, d2)                       
    db2 = np.sum(d2, axis=0)                       

    d1 = np.dot(d2, self.W2.T) * Dsigmoid(self.z1)  
    dW1 = np.dot(self.X.T, d1)                       
    db1 = np.sum(d1, axis=0)                        

    self.W3 -= self.lr * dW3
    self.b3 -= self.lr * db3

    self.W2 -= self.lr * dW2
    self.b2 -= self.lr * db2

    self.W1 -= self.lr * dW1
    self.b1 -= self.lr * db1

#载入模型权重初值
def loadModel():
w = np.load(‘nerve.npz’)
t = Modle()
t.setW(w[‘w1’], w[‘b1’], w[‘w2’], w[‘b2’], w[‘w3’], w[‘b3’])
return t

def train(model, trainX, trainY, isSave = 0):
# 100轮迭代
for epoch in range(100):
# 每次迭代3个样本
for i in range(0, len(trainX), 3):
X = trainX[i:i + 3]
y = trainY[i:i + 3]
loss, _ = model.forward(X, y)
# print(“Epoch:”, epoch, “-”, i, “:”, “{:.3f}”.format(loss)) #输出提示
model.backward()
# 保存模型
if epoch % 100 == 0 and isSave:
np.savez(“nerve.npz”, w1=model.W1, b1=model.b1, w2=model.W2, b2=model.b2, w3=model.W3, b3=model.b3)
return model

三种方法投票， 都不同选第一种

def vote(arr1, arr2, arr3):
res = []
for i in range(len(arr1)):
if arr2[i] == arr3[i]:
res.append(arr2[i])
else:
res.append(arr1[i])
return res

def calCorrectRate(arr1, arr2):
correct = 0
for i in range(len(arr1)):
if arr1[i] == arr2[i]:
correct += 1
return correct / len(arr1)

def showPlt(arr1, arr2):
arr1 = np.array(arr1)
arr2 = np.array(arr2)
plt.rcParams[‘font.sans-serif’]=[‘SimHei’] #用来正常显示中文标签
plt.rcParams[‘axes.unicode_minus’] = False #用来正常显示负号
bar_width = 0.45
name_list = [i for i in range(1,11)]
plt.bar(np.arange(10), 1- arr1, label=‘测试集’,width = bar_width)
plt.bar(np.arange(10)+bar_width, 1 - arr2, tick_label = name_list,label=‘训练集’, width = bar_width)
plt.title(u’交叉验证错误率’)
plt.legend()
plt.show()

#主函数
if name == “main”:

trainDatas,testDatas = CrossVData(10)
cListOfTrain = [] # 交叉验证训练集的准确率数组
correctList = [] # 交叉验证测试集的准确率数组

for j in range(len(trainDatas)):
    print('交叉验证第%d轮' % (j + 1))
    trainX = trainDatas[j][:,0:4]
    trainY = trainDatas[j][:,-1]
    testX = testDatas[j][:,0:4]
    testY = testDatas[j][:,-1]

    #SVM
    svc=svm.SVC(C=100.0, kernel='poly', degree= 2, coef0 = 0.2)
    svc.fit(trainX,trainY)
    testScore = svc.score(testX,testY)
    svmTest = svc.predict(testDatas[j][:,0:4])
    svmTrainTest = svc.predict(trainDatas[j][:,0:4])

    #KNN
    knnTest = []
    knnTrainTest = []
    myTree = creat_kdTree(trainDatas[j], 4, None, 0)
    for i in range(len(testDatas[j])):
        closePoint = np.zeros((3,10))
        closePoint[:,9] = 100000
        findKNode(myTree,closePoint,testDatas[j][i],3)
        knnTest.append(findMaxIndex(closePoint))
    for i in range(len(trainDatas[j])):
        closePoint = np.zeros((3,10))
        closePoint[:,9] = 100000
        findKNode(myTree,closePoint,trainDatas[j][i],3)
        knnTrainTest.append(findMaxIndex(closePoint))
    
    #神经网络
    nerveTest = []
    nerveTrainTest = []
    tTrainY = onehot(trainY, len(trainY))
    # tTestY = onehot(testY, len(testY))

    model = loadModel()
    model = train(model, trainX, tTrainY)
    predictY = model.predict(testX)
    for item in predictY:
        nerveTest.append(reverOneHot(item))
    predictY = model.predict(trainX)
    for item in predictY:
        nerveTrainTest.append(reverOneHot(item))
    
    #三种方法投票
    testScore = vote(nerveTest, svmTest, knnTest)   #测试集
    testScore = calCorrectRate(testScore, testY)

    trainScore = vote(nerveTrainTest, svmTrainTest, knnTrainTest)  #训练集
    trainScore = calCorrectRate(trainScore, trainY)

    print("训练集:", trainScore)
    print("测试集:", testScore)
    correctList.append(testScore)
    cListOfTrain.append(trainScore)
print("测试集平均准确率为：", np.array(cListOfTrain).mean())
print("训练集平均准确率为：", np.array(correctList).mean())

print("测试集平均错误率为：", 1- np.array(cListOfTrain).mean())
print("训练集平均错误率为：", 1- np.array(correctList).mean())
showPlt(correctList, cListOfTrain)