【大道至简】机器学习算法之隐马尔科夫模型HMM详解（1）---开篇：基本概念和几个要素

☕️ 本文来自专栏：大道至简之机器学习系列专栏

❤️各位小伙伴们关注我的大道至简之机器学习系列专栏，一起学习各大机器学习算法

❤️还有更多精彩文章（NLP、热词挖掘、经验分享、技术实战等），持续更新中……欢迎关注我，主页：https://blog.csdn.net/qq_36583400，记得点赞+收藏哦！

个人GitHub地址：https://github.com/fujingnan

欢迎各位小伙伴来到本阶段新模型的学习之旅~接下来我要介绍一下一个非常重要应用非常广泛的模型---隐马尔科夫模型（HMM）的相关原理。该模型我会分四篇文章来讲这个模型，本篇为开篇，主要介绍一下隐马尔科夫模型的基本概念以及模型组成的几个重要元素。

目录

总结

一、概念

二、隐马尔科夫模型三要素

（1）状态序列I、观测序列O

（2）状态转移概率矩阵A、观测概率矩阵B

（3）初始状态概率向量π

三、例子

四、观测序列的生成

五、总结

---

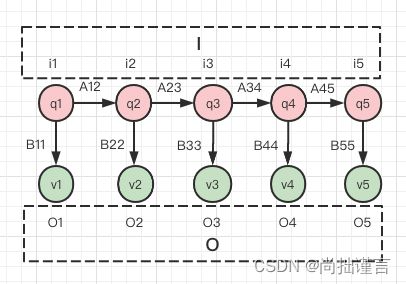
图1 隐马尔科夫模型图示

总结

定义：

结构：状态序列以及对应的状态集合Q，以及每个状态互相转换的概率矩阵A；观测序列O以及对应的观测集合V，以及每个状态下生成每个观测值的概率矩阵B；初始状态向量π。其中，π、A、B三者为隐马尔科夫模型的三要素。

基本作用：有很多时候，我们只能观测到一些现象，却无法知晓产生这种现象的最可能的原因是什么，那么如何通过我们看到的观测结果来反推产生这些观测结果的隐藏原因呢？这往往就是隐马尔科夫模型要做的事。

一、概念

你很喜欢一家甜品店，你几乎每天下班回家都会去买点甜品犒劳一下工作一天后苦逼的自己。但是你发现一个问题：有时候去的时候，排队的人超多（wc，今天这是咋了，人怎么这么多，平时都没这么多人啊，有优惠？emo=生气），有时候去的时候，都没几个人（今天怎么突然人这么少，都不用排队，天冷了大家都不愿意出来？），有时候，人流量就还好（排队人不多，一会儿就排到了）。于是你开始思索，有时候人多，有时候人少，而有时候人流正常，背后一定有什么原因，你跑去咨询了一下商家，商家告诉你，因为每天会有不定量的优惠券发放。那么你能看到的就是人多人少的现象，这在HMM中叫做观测变量，而每天优惠券发放量你不清楚，但客观存在，这在HMM中叫做状态变量，也是我们熟知的隐变量。你通过好几天的观察，得到每天优惠券的发放量并记录下来，就有了状态序列I，得到每一天的人流量并记录下来，就是观测序列O。

你继续观察，发现了两个规律：任意一天优惠券的发放量，都会以一定概率影响到下一天优惠券的发放量，比如，如果某一天优惠券的发放量为20张，那么就有20%的概率使得下一天优惠券的发放量为15张；另一个规律是，不同发放量都会有一定概率导致对应的人流量，比如当优惠券发放量为20时，就会有50%的概率使得今日人流量为30。上述20%在HMM中叫做状态转移概率，50%在HMM中叫做观测概率，进而言之，所有状态转移概率组合起来就形成了状态转移概率矩阵A，所有观测概率组合起来就形成了观测概率矩阵B。

总的来说，隐马尔科夫模型描述了一个由隐藏的马尔科夫链（上述不同优惠券的发放量）随机生成不可观测的状态随机序列（上述一个时间段内实际发生的被你记录下来的每一天优惠券的发放量），再由各个状态生成每一个观测从而产生观测随机序列的过程（上述每天每种优惠券发放量导致对应不同的人流量的现象）。有了这样一个模型，我们就可以通过某一天优惠券的发放量来预测当天排队人数的概率，以及第二天可能的优惠券发放量。

二、隐马尔科夫模型三要素

通过以上感性上的认识，我们大概知道了几个重要的概念：状态序列、观测序列、状态转移概率矩阵、观测概率矩阵。

现在我们从教科书角度再来描述一遍以上概念（我要开始截图了哈）：

（1）状态序列I、观测序列O

说人话就是：某个时间段T内（比如T为7天），每一天都有一个状态i，每一天的状态i都有q1、q2、...、qN几种取值的可能（比如我们说的优惠券发放量可能有5张、10张、15张、20张），每个状态都对应一个出现的可观测的现象o，每个观测都有v1、v2、...、vM几种可能取值（比如1个人排队、5个人排队、10个人排队、15个人排队，20个人排队）。那么，所有q组成的集合，称为状态集合Q，所有v组成的集合称为观测集合V，所有的i组成状态序列I，所有o组成观测序列O，注意这里的i和o不过是对状态和观测的表示，可以认为是变量，其真正有意义的是对应的取值q和v，比如i=q，o=v。

（2）状态转移概率矩阵A、观测概率矩阵B

A是状态转移概率矩阵：

说人话的话就是：a表示如果某一时刻t的状态i(t)等于qi（比如某一天优惠券发放量i等于20张），那么下一时刻t+1的状态i(t+1)的值为qj的概率（下一天优惠券发放量i等于10张的概率）。b表示如果某一时刻t状态的状态i(t)为qj的情况下（比如优惠券发放量i为20张的情况下），其产生的观测o(t)值为vk的概率（导致排队人数o等于30人的概率）。

注意看，A的下标为N*N，因为A是从某一状态转移到另一个状态的概率，而我们的所有可能的状态集合的长度为N，所以这里所有的转移可能性只能是N*N；B的下标是N*M，因为我们的观测结果产生于对应的状态，它的长度只和状态的长度有关，但每一个状态产生的观测结果都有M中可能，所以这里所有观测产生的结果可能性只有N*M。

这里需要注意的是，状态转移是一个状态值的转移，也就是一个时刻的状态在下一时刻可以转移成任意状态，但是对于状态序列来说，是不可以改变的，比如图1中，i1时刻的下一时刻必然是i2，但是它们对应的值，可以是q1转移到q2（i2=q2），也可以是q1转移到q3（i2=q3）等，只不过转换的概率A不同罢了。千万别认为i1时刻可以跳跃转换到i3时刻。观测序列也是一样，q1可以产生v1，也可以产生v3，v4，v5都行，只不过产生不同观测的概率不同罢了，千万别认为q1可以产生下下时刻的v。记住，序列永远是按时间顺序进行的，不能天马行空跳跃！

（3）初始状态概率向量π

这个元素说人话不太好说，因为它更具有数学意义，隐马尔科夫模型中，在我们进行后续概率迭代计算时，必然有个冷启动问题，所以我们会随机初始化一个概率分布，以它为基石进行迭代。

通过以上分析，我们来总结一下构成隐马尔科夫模型的所有涉及到的元素：

状态相关：状态序列I（变量表示）、状态集合Q（变量值）、状态转移概率矩阵A、初始状态概率向量π；

观测相关：观测序列O（变量表示）、观测集合V（变量值）、观测概率矩阵B；

而隐马尔科夫模型的数学表示λ=(π，A，B)，所以，π、A、B称为隐马尔科夫模型的三要素。

三、例子

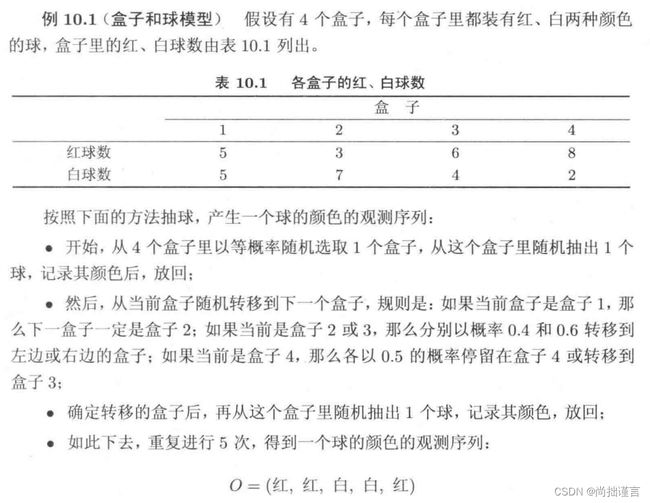
我们通过《统计学习方法》中的例子进一步加强理解。例子是这样的（我又要截图了哈）：

对照我们上文中将的概念，这里我们抽过的并记录下来的盒子的编号，排成一排就是我们的状态序列， 由于这里抽了5次，所以状态序列I的长度为5：

i1=盒子？

i2=盒子？

i3=盒子？

i4=盒子？

i5=盒子？

I=(i1, i2, i3, i4, i5)

上述盒子后的问号“？”是因为对于观测者的我们来说，最终只能看到取出的球的颜色序列，而并不知道每个球是从哪个盒子里取出的，所以盒子就是隐藏的状态序列。

我们的盒子一共有4种：q1=盒子1，q2=盒子2，q3=盒子3，q4=盒子4，所以，状态集合为：

Q=(盒子1, 盒子2, 盒子3, 盒子4)

我们抽到一个盒子后，取出一个球，观察其颜色并记录，那么这个颜色的球就是我们的观测值v，例子中，最终的观测序列为：

O=(红，红，白，白，红)

因为我们笼统就红色和白色两种颜色的球，所以观测集合V=(v1=红，v2=白) 

即i1=盒子？的情况下，产生的观测变量o1的值v1=红，i2=盒子？的情况下，产生的观测变量o2的值v1=红，以此类推。可以看到，i2是i1的下一时刻，但其观测变量o2的值仍然为v1。

正如例子中所述：如果取得的盒子编号为1，那么下一次必然取得盒子2，所以盒子1转移到盒子2的概率为1，转移到其它盒子的概率为0：

[0, 1, 0, 0]

如果取得的盒子编号为2，那么下一次会有0.4的概率取到编号为1的盒子或者有0.6的概率取到编号为3的盒子：

[0.4, 0, 0.6, 0]

如果取得的盒子编号为3，那么下一次会有0.4的概率取到编号为2的盒子或者有0.6的概率取到编号为4的盒子：

 [0, 0.4, 0, 0.6]

如果取得的盒子编号为4，那么下一次会有0.5的概率又取到自己或者有0.5的概率取到盒子3：

 [0, 0, 0.5, 0.5]

将上述取来取去的所有概率组合起来，就得到了我们的状态转移概率矩阵：

它是N*N的矩阵，每一行的行号表示当前取得盒子的编号，列号表示转移到下一次取得盒子的编号，矩阵元素值表示取得当前行号值的盒子后，下一轮会取得对应列号值的盒子的概率。

又通过例子中的表格可以知道，每一个盒子（状态）下可能取得的每种颜色球（观测）的概率：比如盒子1中，有5个红球5个白球，那么在取得盒子1的状态下，再从盒子1中抽一个球，显然抽中红球和白球的概率都为5/(5+5)=0.5，同理可得所有状态下所有观测概率值，组合起来就得到观测概率矩阵了：

最后，我们需要假设一个初始状态概率向量，也就是在第一次取盒子之前的一个隐藏的初始状态概率，学过物理吧，就好比将一个有重力的物体举高高，在还没将它丢下的时候，它已经存在一个初始势能了，只不过这里我们并不知道这个初始状态是啥，所以我们要随机初始化一个，后面通过迭代计算出来就行。

π=(0.25, 0.25, 0.25, 0.25)

如果现在不理解这个π没关系，随着我们对模型讲解的深入，后面会明白它的作用的。

四、观测序列的生成

通过上述分析，我们并不是很严谨的能够感受到，观测序列对我们而言看上去很有意义，因为它是我们肉眼可见，并具有实际意义。从模型的定义上看也可以看出，模型的三要素并没有包括观测序列（当然我们也没有状态序列，这个我们后面的文章会讲到），这也可以认为是该模型目的是让我们通过模型参数，来预测“将要发生什么”。因此接下来我们来看一下隐马尔科夫模型下观测序列是怎么生成的。

假如我们已经通过学习得到了一个隐马尔科夫模型λ=(A, B, π)，那么我们观测序列生成的过程是：通过初始状态分布，来产生第一个状态，并由第一个状态的值以及观测概率来计算第一个观测结果的值，再由第一个状态的值通过状态转移概率计算得到第二个状态的值， 并由第二个状态的值以及观测概率来计算第二个观测结果的值……以此类推，以至于整个观测序列为止。

五、总结

通过以上内容，我们已经很清楚的了解了隐马尔科夫模型是个什么东东了，包括它的定义，结构，含义。

定义：

结构：状态序列以及对应的状态集合Q，以及每个状态互相转换的概率矩阵A；观测序列O以及对应的观测集合V，以及每个状态下生成每个观测值的概率矩阵B；初始状态向量π。其中，π、A、B三者为隐马尔科夫模型的三要素。

既然明白了隐马尔科夫模型的基本面貌，那么该如何学习建模它呢？如何通过计算来分析某个状态序列下出现的对应观测序列的概率呢？毕竟我们给出一个出现的观测序列后，是需要告诉别人这种情况出现的概率是多大，不然也没有意义了。还有，当我们看到了出现的某个观测序列后，如何能知道它是由哪种状态序列生成的呢？毕竟我们在知道某个现象后，更希望知道产生这种现象的最可能的原因是什么。

以上三种灵魂拷问就涉及到隐马尔科夫模型最最最重要的三种基本应用，即隐马尔科夫模型的3个基本问题：学习问题、概率计算问题、预测问题。注意这3个基本问题在面试过程中，有很大概率会被问到。那么接下来我会通过3篇文章来分别讨论这三种问题的解决方法，关注我，不要错过~