【故障诊断】基于贝叶斯优化支持向量机的轴承故障诊断附matlab代码

 1 内容介绍

贝叶斯网络(Bayesian Network或BN)是人工智能领域进行建模和不确定性推理的一个有效工具。贝叶斯网推理的基本任务是：给定一组证据变量观察值，通过搜索条件概率表计算一组查询变量的后验概率分布。在现实应用中，观察到的证据值可以为任意值，即证据值可能不包含在条件概率表中。因此，有必要提出一种在给定任意证据值时都能计算后验概率分布的方法。针对这个问题，本文主要讨论了带学习功能的贝叶斯网的构造和推理：当从样本中构造贝叶斯网结构时，也从样本中学习极大似然参数(极大似然假设)，用以取代相应的条件概率表，即把极大似然参数看作是贝叶斯网的一部分。　　 使用传统方法从样本中构造了贝叶斯网结构之后，本文主要关注如何从样本中学习极大似然参数。贝叶斯网中包含两种推理方法：正向推理和反向推理。对于正向推理，我们提出了基于支持向量机和Sigmoid函数来学习极大似然参数的方法。对于反向推理，首先基于贝叶斯公式，把反向推理问题转化为正向推理问题；然后对极大似然参数进行线性插值。　　 然而，对于已经构造完的贝叶斯网，它们很可能没有原始样本。针对这种情况，本文提出了把现有条件概率表映射成样本的方法，进而从得到的样本中学习极大似然假设。　　 进一步，为应用带有极大似然假设的贝叶斯网进行近似推理，本文给出了相应的Gibbs采样算法。　　 最后，我们给出一个应用实例，并给出了测试学习极大似然假设算法精度和验证Gibbs采样算法收敛性的实验。初步实验结果表明我们的方法是可行的。　

　 本文的主要贡献如下：　　 ●本文提出了学习带有学习功能的贝叶斯网的方法，即当使用现有方法从样本中构造贝叶斯网结构时，基于支持向量机和Sigmoid函数，也从样本中学习极大似然假设，用以取代相应的条件概率表。然后基于带有极大似然假设的贝叶斯网，本文进一步提出了相应的正向和反向推理方法。这解决了给定任意证据值都能进行推理的问题。　　 ●本文提出了把现有条件概率表映射成样本的方法，实现了从现有条件概率表中也能学习极大似然假设，解决了对于已经构造完的贝叶斯网(可能没有原始样本)，给定任意证据值也能进行推理的问题。　　 ●进一步，为应用带有极大似然假设的贝叶斯网进行近似推理，本文给出了相应的Gibbs采样算法。一点程度上解决了贝叶斯网精确推理的低效问题。​

2 仿真代码

clc
clear all
close all
addpath(genpath(pwd))

% 生成3类样本（二维高斯分布）?
sigma = [0.6 0; 0 0.6];
numData = 100;

mu = [6 5];
X_1 = mvnrnd(mu, sigma, numData);
label_1 = ones(numData, 1);

mu = [3 9];
X_2 = mvnrnd(mu, sigma, numData);
label_2 = 2*ones(numData, 1);

mu = [-2 7];
X_3 = mvnrnd(mu, sigma, numData);
label_3 = 3*ones(numData, 1);

data = [X_1; X_2; X_3];
label = [label_1; label_2; label_3];

%% 贝叶斯优化参数

% 变量的上下限以及类型设置
c =  optimizableVariable('c',  [1e-2 1e2], 'Type', 'real');
g =  optimizableVariable('g',  [2^-7 2^7], 'Type', 'real');
parameter = [c, g];

% 交叉验证参数设置（关闭交叉验证时设置为[]）?
kfolds = 5;
% kfolds = [];

%  目标函数
objFun = @(parameter) getObjValue(parameter, data, label, kfolds);

% 贝叶斯优化
iter = 30;
points = 10;
results = bayesopt(objFun, parameter, 'Verbose', 1, ...
                   'MaxObjectiveEvaluations', iter,...
                   'NumSeedPoints', points);
% 优化结果
[bestParam, ~, ~] = bestPoint(results, 'Criterion', 'min-observed');

%% 利用最优参数重新训练SVM模型
c = bestParam.c;  
g = bestParam.g; 

% 训练和测试
cmd = ['-s 0 -t 2 ', '-c ', num2str(c), ' -g ', num2str(g), ' -q'];
model = libsvmtrain(label, data, cmd);
[~, acc, ~] = libsvmpredict(label, data, model); 

%% SVM边界可视化?
d = 0.02;
[X1, X2] = meshgrid(min(data(:, 1)):d:max(data(:, 1)), min(data(:, 2)):d:max(data(:, 2)));
X_grid = [X1(:), X2(:)];
grid_label = ones(size(X_grid, 1), 1);
[pre_label, ~, ~] = libsvmpredict(grid_label, X_grid, model);

% 缁樺埗鏁ｇ偣鍥?
figure
color_p = [150, 138, 191;12, 112, 104; 220, 94, 75]/255; % 鏁版嵁鐐归鑹?
color_b = [218, 216, 232; 179, 226, 219; 244, 195, 171]/255; % 杈圭晫鍖哄煙棰滆壊
hold on
ax(1:3) = gscatter(X_grid (:,1), X_grid (:,2), pre_label, color_b);

% 缁樺埗鍘熷鏁版嵁鍥?
ax(4:6) = gscatter(data(:,1), data(:,2), label);
set(ax(4), 'Marker','o', 'MarkerSize', 7, 'MarkerEdgeColor','k', 'MarkerFaceColor', color_p(1,:));
set(ax(5), 'Marker','o', 'MarkerSize', 7, 'MarkerEdgeColor','k', 'MarkerFaceColor', color_p(2,:));
set(ax(6), 'Marker','o', 'MarkerSize', 7, 'MarkerEdgeColor','k', 'MarkerFaceColor', color_p(3,:));
set(gca, 'linewidth', 1.1)
title('Decision boundary (gaussian kernel function)')
axis tight
legend('off')
box on
set(gca, 'linewidth', 1.1)

% This make.m is for MATLAB and OCTAVE under Windows, Mac, and Unix
function make()
try
    % This part is for OCTAVE
    if (exist ('OCTAVE_VERSION', 'builtin'))
        mex libsvmread.c
        mex libsvmwrite.c
        mex -I.. libsvmtrain.c ../svm.cpp svm_model_matlab.c
        mex -I.. libsvmpredict.c ../svm.cpp svm_model_matlab.c
    % This part is for MATLAB
    % Add -largeArrayDims on 64-bit machines of MATLAB
    else
        mex CFLAGS="\$CFLAGS -std=c99" -largeArrayDims libsvmread.c
        mex CFLAGS="\$CFLAGS -std=c99" -largeArrayDims libsvmwrite.c
        mex CFLAGS="\$CFLAGS -std=c99" -I.. -largeArrayDims libsvmtrain.c ../svm.cpp svm_model_matlab.c
        mex CFLAGS="\$CFLAGS -std=c99" -I.. -largeArrayDims libsvmpredict.c ../svm.cpp svm_model_matlab.c
    end
catch err
    fprintf('Error: %s failed (line %d)\n', err.stack(1).file, err.stack(1).line);
    disp(err.message);
    fprintf('=> Please check README for detailed instructions.\n');
end
选对路径的基础上，运行Feature_extraction.m即可；
如果运行时发生报错说没有libsvmtrain函数，可以先运行BO-SVM文件夹里面的main函数，导入libsvm库就没有问题啦！
其中包括网格搜索、遗传算法、贝叶斯优化算法三种算法优化支持向量机；
采用的数据是美国西储大学的滚动轴承数据；
 

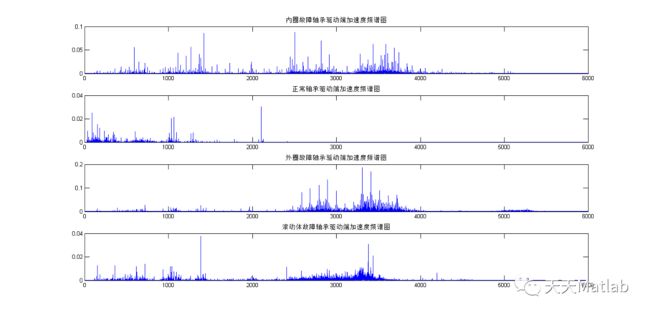
3 运行结果

4 参考文献

[1]王君宇. 基于小波包和优化支持向量机的滚动轴承故障诊断研究. 

[2]苏小杰. 大规模数据下基于支持向量机的轴承故障诊断研究.

[3]杨正友, 彭涛, 李健宝,等. 基于贝叶斯推断LSSVM的滚动轴承故障诊断[J]. 电子测量与仪器学报, 2010, 24(5):5. 

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。