深度学习之【pytorch入门】——二文带你理解深度学习的概念
深度学习神经网络基础
文章目录
- 深度学习神经网络基础
-
- 什么是监督学习和无监督学习?
- 监督学习中的两大问题
-
- 回归问题
- 分类问题
- 模型的欠拟合和过拟合
- 拟合
-
- 欠拟合
- 过拟合
- 什么是向前传播?什么是向后传播
-
- 前向传播
- ⋆ \star ⋆后向传播
- 什么是损失函数?
-
- 常用损失函数
- 什么是优化函数?
- 什么是激活函数?
-
-
- 常用的三种非线性激活函数
-
什么是监督学习和无监督学习?
监督学习:通过输入一组数据和其对应的标签数据让模型进行学习,找到输入和输出之间的最优映射关系。模型利用预测出来的映射关系进行预测。可以理解为有人在监督你学习,你在这边学,等你学完了就有人能告诉你答案的感觉。
无监督学习:通过输入一组数据但并不提供标签数据,让模型进行训练,我们对整个训练过程不做干涉,最后让模型自己发现数据之间的隐藏特征和映射模型。可以理解为自学,没有人监管你,没人给你答案参考,通过自己摸索题目之间的关系来学习。
监督学习中的两大问题
回归问题
回归是指让模型训练输入的数据并对未训练过的数据进行预测,训练所得到的是一个线性连续的对应关系。可以理解为模型自己通过输入和输出反推出之间的函数关系。例如:给你x=1,2,3,4、y=2,4,6,8,通过这几个数据你就会猜测x和y的关系是y=2x,而训练也就是这个过程。
最终拟合出来的是一个线性连续映射关系(你可以理解为函数)。
分类问题
分类是让我们搭建的模型经过训练之后建立起一个离散的映射关系,与回归最本质的区别就是最后得到的映射关系是离散的。如果这个结果只有0和1,那就叫二分类模型。
还有可能是多分类的问题。
模型的欠拟合和过拟合
- 首先说明一下模型训练的原理:
通过模型对我们所输入(x)和提供的标签(y)进行对比,并猜测(推断出)x和y之间的映射关系(理解为函数)。
从函数图像显示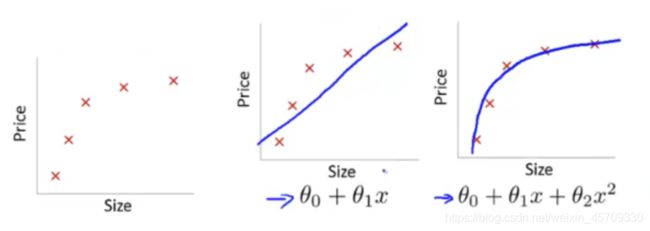
分布在实线周围的点就是模型的预测,通过对比猜测结果和实际真实情况可以得出,如果预测点离这些实线很近,说明越符合实际的情况,误差也就越小,也就是越拟合。我们可以把拟合理解为预测与实际情况的吻合程度。但如果偏差太大就说明误差很大,与实际情况不符。(产生误差的原因,公式、计算机计算、电脑算力等)(这种也类似于线性回归,一个个散点分布在实线周围)
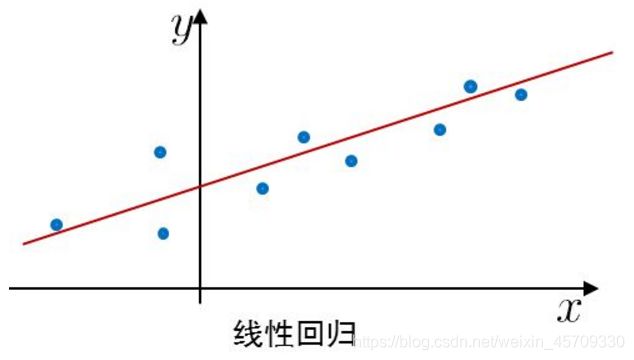
拟合
欠拟合
可以理解为预测与实际相差很大,预测点在实际情况的曲线上动荡幅度较大,与实际不符
解决方案:
- 手动添加准确方案,也就是添加特征项。我们加入与原数据具有相关性的数据来对模型进行纠正。
- 构造复杂多项式。造成这种原因可能是因为我们的给的数据之间太过于集中,有大部分不能吻合,所以我们要构造更复杂的多项式来让模型尽可能的预测到。(有点类似泰勒展开,展开的越多,越接近于真实的结果)
- 减少正则化参数。正则化参数是为了防止过拟合的情形,如果出现了欠拟合说明正则化参数太多了,应该减少一点(什么是正则化参数?)
过拟合
通俗理解:
因为可能会出现并不是我这个模型判断出来的结果,可能只是我把标签泄露给了模型。
相当于就是高考,我们就是老师,模型就是学生,训练集就是平时的小测试,有效集就是平时的模拟考,测试集就是真正高考
平时训练完了之后进行模拟测试,那么此时如果他只是在训练集里面正好只是背下了答案,但其实根本不会去判断,到真正去高考的时候就做不对了
这样就会导致过拟合,就是没实际学习到,只是背答案而已
测试集是不能够泄露给模型的,简单来说测试集就是一次考试,只要知道了答案再怎么做也不是考试。
验证集就是为了验证,比如:如果有几个学生经过同一个训练集训练,在你提问他一个问题的时候:一个歪歪扭扭的3,下面的同学就开始猜了,猜5,1,3,7,你就看到第三个同学对了
你可能就会比较喜欢这个同学,但是其实是有可能他对这个测试集正好匹配得比较好。所以这里就会产生不同,到底是因为他真的厉害,还是因为他正好猜对了
因为我们是能知道答案的,当我们看到一个猜对了的同学之后,就会带上个人感情,就很喜欢这个同学,但是这其实间接地把答案泄露给了同学,就会导致他做的会很符合我们的预期
因为我们已经知道答案了,所以,我们要排除掉个人感情,因此要排除这种可能就要引入验证集,验证集我们能够知道答案,而测试集我们和模型都不能知道答案。
而且不能用测试集跑太多次,跑太多次就也会变成训练集了,测试集只能跑一次
还有一个例子就是股票,(设现在为2019.1.1)如果要预测股票,就要给他2017.1.1之前的数据,要预测2017之后的数据,不同的模型产生不同的因子来预测2017年之后的然后将预测的好的去跑2019.1.1之后的,还未发生的,然后在预测现实发生过的2019.1.1之后的时候准确率就会大大下降,这个就是**过拟合。
解决方案
- 增大训练的数据量:在训练集中添加未过的图像。
- 增加正则化参数
- Dropout方法:在神经网络模型前向传播的过程,随机丢弃一些参数。
什么是向前传播?什么是向后传播
前向传播
参考我的上一篇博客:深度学习之【pytorch入门】——一文带你理解深度学习的概念
里面提到的就是向前传播。
前向传播就是将数据输入到神经网络中,然后对其在各个神经元处进行加权平均。这样就完成了一次传递,通过第一层求好的平均数再次求加权平均就传到了第二层,以此类推(套娃)。然后每次传递到下一层就进行一次激活,相当于人脑中的激活神经元。通过不断计算,最后在输出层中输出。
⋆ \star ⋆后向传播
可以理解为是对模型中的参数进行微调,通过多次向后传播也就是多次微调得到最优的参数组合,也就是最优解。
向后传播是对向前传播的一个微调处理。
这个微调处理就是对向前传播的计算函数求偏导(所有的变量都要求),每轮向后传播都用这三个值来微调参数。
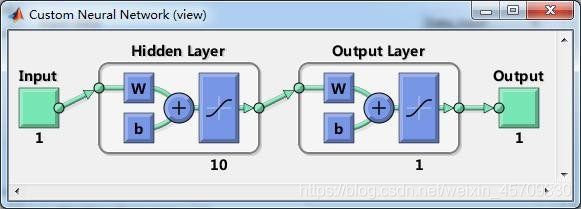
参考一下初级神经网络的例子
什么是损失函数?
损失可以理解为是描述预测和实际的差距,也表示了我们的模型是不是具有预测的能力。
优化可以理解为是在不过拟合的情况下减少预测与实际的差距。
常用损失函数
- 均方误差函数(MSE)(类似于方差的计算)
M S E = 1 N ∑ i = 1 N ( y t r u e i − y p r e d i ) 2 MSE=\frac{1}{N}\sum^{N}_{i=1}(y_{true_i}-y_{pred_i})^2 MSE=N1i=1∑N(ytruei−ypredi)2
可以理解为反映了预测点在实际曲线周围的偏离程度。
- 均方根误差函数(RMSE)(类似于标准差的计算)
R M S E = 1 N ∑ i = 1 N ( y t r u e i − y p r e d i ) 2 RMSE=\sqrt{\frac{1}{N}\sum^{N}_{i=1}(y_{true_i}-y_{pred_i})^2} RMSE=N1i=1∑N(ytruei−ypredi)2
可以理解为反映了预测点在实际曲线周围的偏离程度的开方
- 平均绝对误差函数(MAE)(类似于两点间的距离)
M A E = 1 N ∑ i = 1 N ∣ ( y t r u e i − y p r e d i ) ∣ MAE=\frac{1}{N}\sum^{N}_{i=1}|(y_{true_i}-y_{pred_i})| MAE=N1i=1∑N∣(ytruei−ypredi)∣
可以理解为反映了预测值与真实值的距离
以上均是值越小越好。
什么是优化函数?
跟向后传播类似。但我们还要想,如何对参数进行初始化、参数怎么微调、合适的学习率是多少的问题
优化函数就是一个解决上面三个问题的集合
优化过程中求解的就是参数的一阶偏导。
那么要优化函数,我们就要调整权重,使权重落在错误率最小的点。
那么我们就通过梯度来找到这个错误率最小的点。
![]()
![]()
梯度:详见百科
个人理解:梯度就是通过对其求各个方向的变化率(即偏导数),再通过向量来表示这个下降的趋势。
即这里的梯度表示就是将多元函数的各个参数求得的偏导数以向量的形式表示出来。即可以表示为
z = f ( x , y ) 的 偏 导 数 ∂ f ∂ x 、 ∂ f ∂ y , 则 梯 度 为 g r a d f ( x , y ) = ∂ f ∂ x i ⃗ + ∂ f ∂ y j ⃗ = ( ∂ f ∂ x , ∂ f ∂ y ) z=f(x,y)的偏导数\frac{\partial f}{\partial x}、\frac{\partial f}{\partial y},则梯度为gradf(x,y)=\frac{\partial f}{\partial x}\vec{i}+\frac{\partial f}{\partial y}\vec{j}=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}) z=f(x,y)的偏导数∂x∂f、∂y∂f,则梯度为gradf(x,y)=∂x∂fi+∂y∂fj=(∂x∂f,∂y∂f)
-
梯度下降公式
θ j = θ j − η ∂ J ( θ j ) ∂ θ j \theta_j=\theta_j-\eta\frac{\partial J(\theta_j)}{\partial \theta_j} θj=θj−η∂θj∂J(θj)
这里的训练样本总数为 j j j, j = 0... n j=0...n j=0...n这里的等号看作编程的赋值运算。 θ \theta θ是优化的对象, η \eta η是学习速率, J ( θ ) J(\theta) J(θ)是损失函数, ∂ J ( θ j ) ∂ θ j \frac{\partial J(\theta_j)}{\partial \theta_j} ∂θj∂J(θj)是根据损失函数来计算的梯度。
学习速率是梯度更新的快慢如果学习速率过快,更新跨步就会变大,容易出现局部最优和抖动(因为梯度更新过快导致有一部会比较准确,另一部分就可能没训练得那么准确),学习速率过慢,梯度迭代次数会增加(也就是一次梯度使用多次),参数优化时间会更长。 -
批量梯度下降公式
θ j = θ j − η ∂ J b a t c h ( θ j ) ∂ θ j \theta_j=\theta_j-\eta\frac{\partial J_{batch}(\theta_j)}{\partial \theta_j} θj=θj−η∂θj∂Jbatch(θj)
可以理解为分组训练,我们平时一般都是分组训练才比较有效率,也更有效
将整个训练集划分为若干组,每个组数量相同,其中一个组就是一个批量,每次都以一组数据来对模型进行训练,并以这个组计算得到的损失值为基准对模型中所有的参数进行梯度更新。样本总数为 b a t c h = 0... b a t c h batch=0...batch batch=0...batch
- 随机梯度下降公式
θ j = θ j − η ∂ J s t o c h a s t i c ( θ j ) ∂ θ j \theta_j=\theta_j-\eta\frac{\partial J_{stochastic}(\theta_j)}{\partial \theta_j} θj=θj−η∂θj∂Jstochastic(θj)
可以理解为随机选取训练集中的一部分进行训练,每次都是随机选取
什么是激活函数?
之前我们在学习感知机的时候也接触到了激活函数,激活函数就是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。
输入的 inputs 通过加权,求和后,还被作用了一个函数,这个函数就是激活函数。
引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。
可以理解为激活函数是一个能够将数据送入我们的神经网络里面去的一个函数,再让输入的值变得更加非线性,因为我们生活很多问题都是非线性的,引入这个激活函数能够使其更加非线性,能够解决更多方面层次的问题。
(单层神经网络)激活函数一般式为:
f ( x ) = W ⋅ X + b f(x)=W\cdot X +b f(x)=W⋅X+b
其中 X X X为输入的数据, b b b为偏置(也就是激活函数在y轴上的截距。)(这个就类似于一次函数(一次函数线性的))。有偏置能够让模型具有更强的变换能力,对各种不同的情况都能处理。
可以理解为偏置使得这个这个激活函数更加一般化,因为经过原点是一种特殊的情况
如果有多层神经网络就对这个函数进行迭代。(通俗来说就是套娃)就是将第一层得到的值再次作为输入代入到激活函数里面,有几层就代几次。
常用的三种非线性激活函数
-
Sigmoid
f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
图像为: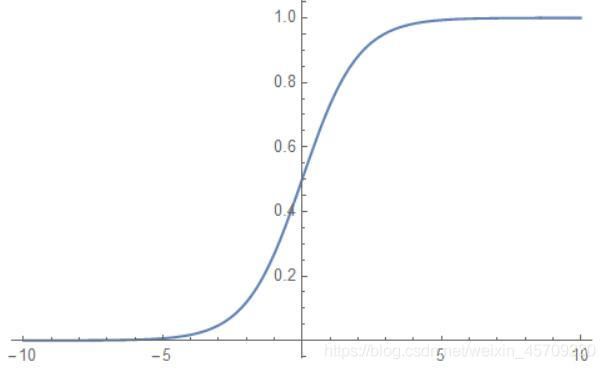
函数特点:这个函数导数最大值为 1 4 \frac{1}{4} 41,也就是每向后传播一次,梯度变为原来的四分之一,如果模型层次太多,会导致梯度消失。这个函数恒大于0,导致收敛速度变慢,我们要尽量选取零中心数据,即比较像线性的那段。 -
ReLU
f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x)
图像为: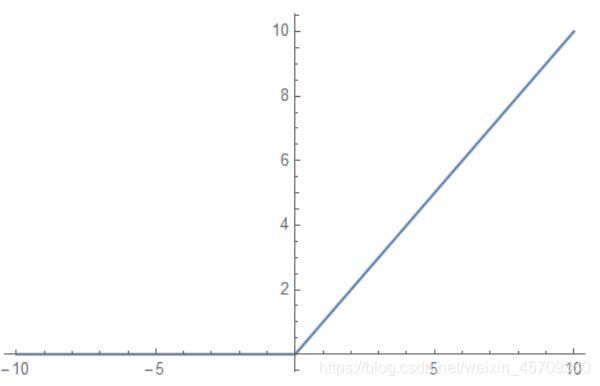
函数特点:收敛速度快,计算效率高,但可能会导致某些神经元永远不会被激活,使用这个函数应用Adam算法和Xavier初始化方法。
资料:http://www.qianjia.com/html/2018-06/20_295742.html