MATLAB R2018b学习笔记（7）

系列文章目录

第1章 MATLAB R2018b环境
第2章 MATLAB 数值计算
第3章 MATLAB符号计算
第4章 MATLAB计算的可视化和GUI设计
第5章 MATLAB程序设计
第6章 线性控制系统分析与设计
第7章 Simulink仿真环境
第8章 MATLAB高级应用

---

---

第二章、MATLAB数值计算

---

前言

MATLAB是 Matrix Laboratory即矩阵实验室的缩写。MATLAB最基本也是最重要的功能就是进行实数或复数矩阵的运算。

---

7、矩阵和数组

7.1矩阵输入

在MATLAB中的矩阵表示应遵循以下基本常规。
(1）矩阵元素应用方括号([ ]）括住。
(2）每行内的元素间用逗号或空格隔开。
(3）行与行之间用分号或回车键隔开。
(4）元素可以是数值或表达式。
1．通过显式元素列表输入矩阵
对于比较小的简单矩阵，可以通过显式元素列表直接用键盘输入矩阵。

对于较为复杂的矩阵，为了使输入方式更符合用户习惯，可以用回车键代替分号分隔行。大部分试验数据都用这种形式处理，通常，简单地将左、右括号加在试验数据前后来得到矩阵。
2.通过语句生成矩阵
通过语句生成矩阵有以下几种方式。
(1）使用from:step:to方式生成行向量。如果是线性等间距格式的向量，则可以使用“from:step:to”方式生成。
语法:
from:to
from:step:to
说明:from、step和 to分别表示开始值、步长和结束值。当step 省略时则默认为step=1;当step省略或step>0而from>to时为空矩阵;当step<0而from (2）使用linspace和 logspace函数生成向量。
①linspace用来生成线性等分向量。与“from:step:to”方式不同的是，它直接给出元素的个数从而得出各个元素的值。
语法:
linspace(a,b,n)
说明:a、b、n 3个参数分别表示开始值、结束值和元素个数。生成从a到b之间线性分布的n个元素的行向量,n如果省略则默认值为100。

②logspace用来生成对数等分向量，它和linspace一样直接给出元素的个数从而得出各个元素的值。在画Bode图等应用中，需要使用logspace命令生成对数等间隔的数据。
语法:
logspace(a,b,n)
说明: a、b、n 3个参数分别表示开始值、结束值和数据个数，n如果省略则默认值为50。生成从10的a次幂到10的b次幂之间按对数等分的n个元素的行向量。

3.由函数产生特殊矩阵
MATLAB提供了很多能够产生特殊矩阵的函数，各函数的功能如下表所示。
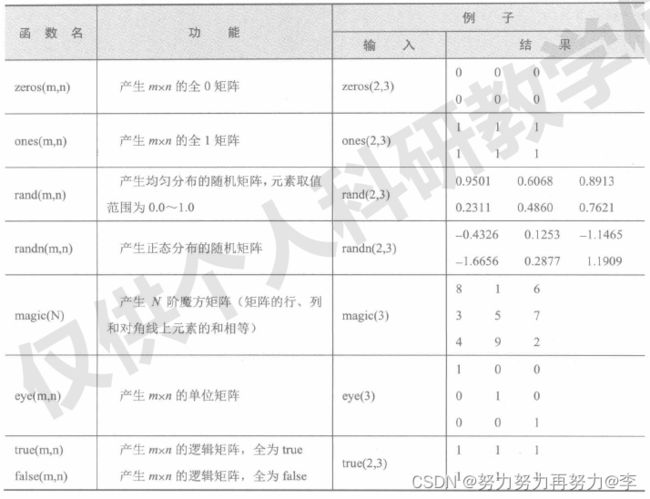说明:当zeros、ones、rand、randn和 eye函数中只有1个参数n时，则为nxn的方阵。

7.2矩阵元素

矩阵和多维数组都是由多个元素组成的，每个元素通过下标来标志。
1．矩阵的下标
以下介绍矩阵的下标方式。
(1）全下标方式。矩阵中的元素可以用全下标方式标志，即由行下标和列下标表示，l个mxn的A矩阵的第i行第j列的元素表示为A(i,j)。例如“A(3,2)=6”表示在矩阵A的“第3行第2列”的元素赋值为6。
如果在提取矩阵元素值时，矩阵元素的下标行或列(i,j)大于矩阵的大小(m,n)，则MATLAB会提示出错;而在给矩阵元素赋值时，如果行或列(i,j)超出矩阵的大小(m,n)，则MATLAB自动扩充矩阵，扩充部分以0填充。

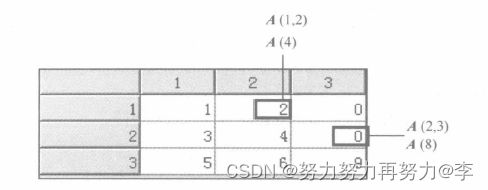
(2）单下标方式。矩阵元素也可以用“单下标”标志，就是先把矩阵的所有列按先左后右的次序连接成“一维长列”，然后对元素位置进行编号。以mxn的矩阵A为例，若元素A(i,j)则对应的“单下标”为s=(j-1)x m+i。矩阵A的元素下标如下图所示。
2．子矩阵块的产生方式
MATLAB利用矩阵下标可以产生子矩阵。对于a(i.j)，如果i和j是向量而不是标量，则将获得指定矩阵的子矩阵块。子矩阵是从对应矩阵中取出一部分元素构成的，如下图所示，分别用全下标和单下标方式取子矩阵。

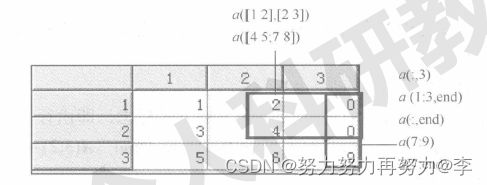
(1）用全下标方式。矩阵A如上图所示，使用以下几种方式都可以构成子矩阵。
①a([1 3],[2 3]):取行数为1、3，列数为2、3的元素构成子矩阵。
②a(1:3,2:3):取行数为1～3，列数为2~3的元素构成子矩阵，“1:3”表示1、2、3行下标。
③a(:,3):取所有行数，即为1~3，列数为3的元素构成子矩阵，“:”表示所有行或列。
④a(1:3,end):取行数为1~3，列数为3的元素构成子矩阵，用“end”表示某一维数中的最大值，即3。
(2）用单下标方式。
a([1 3;26]):取单下标为1、3、2、6的元素构成子矩阵。
(3）逻辑矩阵。子矩阵也可以利用逻辑矩阵来标志，逻辑矩阵是指大小和对应矩阵相同，而元素值为0或者1的矩阵。可以用a(l1,l2)表示子矩阵，其中l1、l2为逻辑向量，当l1、l2的元素为0则不取该位置元素，反之则取该位置的元素。
3．矩阵的赋值
矩阵的赋值有几种方式:全下标方式、单下标方式和全元素方式。
①全下标方式: A(i,j)= B，给A矩阵的部分元素赋值，则B矩阵的行列数必须A矩阵的行列数。
②单下标方式:A(s)=b，b为向量，元素个数必须等于A矩阵的元素个数。
③全元素方式:A(:)=B，给A矩阵的所有元素赋值则B矩阵的元素总数必须等于A矩阵的元素总数，但行列数不一定相等。
4．矩阵元素的删除操作
在MATLAB中可以对矩阵的单个元素、子矩阵块和所有元素进行删除操作，方法就是简单地将其赋值为空矩阵（用[]表示)。
5.生成大矩阵
在MATLAB中，可以通过方括号（[ ]）将小矩阵联结起来生成1个较大的矩阵。
6.矩阵的翻转
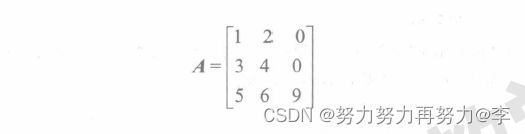
MATLAB中可以通过功能强大的矩阵翻转函数对矩阵进行翻转,其功能如下表所示。假设矩阵A同上例。

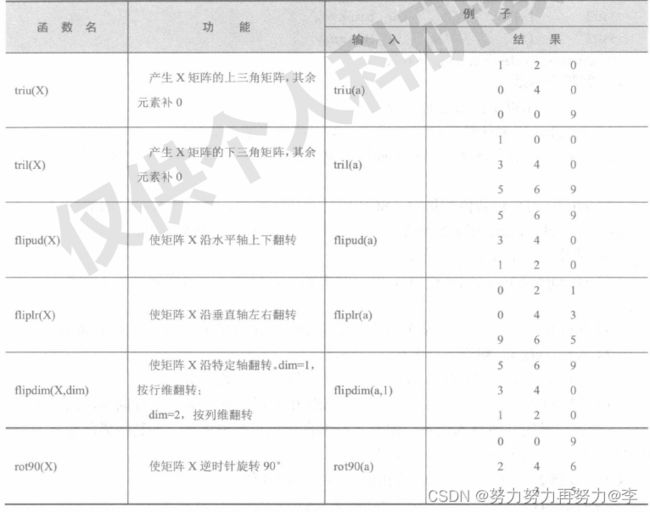
7.3字符串

在MATLAB中，字符串是作为字符数组引入的，一个字符串由多个字符组成并按行向量进行存储，用单引号(‘'）界定。而其中的每一字符(包括空格）都是以其ASCIl码的形式存放的，只是其外显形式仍然是可读的字符。
1．字符串占用的字节
由于MATLAB在存储字符串时，每一个字符会占用2字节，用whos命令查看字符串变量所占用的存储空间,可以看到Bytes为 Size的2倍。

2.字符串函数
字符串可以用以下函数进行运算。
( 1 ) length(strl):用来计算字符串的长度（即组成字符的个数)。
( 2) double(strl):用来将字符型转换成以ASCII 码为数值的 double型，包括空格（ASCII码为32)。
( 3)char(strl):用来将数值型按照ASCII码转换成字符型，省略小数点后的数据。
(4)class或ischar:用来判断某一个变量的类型。class函数返回char则表示为字符串，而ischar函数返回1表示为字符串。
(5) strcmp(x,y):比较字符串x和y 的内容是否相同。返回值如果为1则相同，为0则不同。
(6) findstr(x,xl):寻找在某个长字符串x中的子字符串xl，返回其起始位置。
(7) deblank(x ):删除字符串尾部的空格。
(8 ) eval(x):执行字符串，可以将字符串型转换成为数值型。
由于MATLAB将字符串以其相对应的ASCII码形式存储成1个行向量，因此字符串可以进行行向量的任何算术运算;如果字符串直接进行数值运算，则其结果就变成一般数值向量的运算，而不再是字符串的运算。
3.使用1个变量存储多个字符串
有如下几种方法使用1个变量存储多个字符串。
(1）使用多个字符串组成1个新的行向量，将多个字符串变量直接用逗号(,)连接。
(2）使用矩阵。将每个字符串放在1行，多个字符串可以构成1个二维字符数组，但必须先在短字符串结尾补上空格符，以确保每个字符串（即每一行）的长度一样。
(3）使用str2mat、strvcat和 char函数。使用专门的str2mat、strvcat和 char函数可以构造出字符串矩阵，而不必考虑每行的字符数是否相等，总是按最长的字符串进行设置，不足的字符串的末尾用空格补齐。
4.执行字符串
如果需要直接“执行”某一字符串，可以使用eval命令。

5.显示字符串
字符串可以直接使用disp命令显示出来，即使后面加分号(;）也可以显示。

7.4矩阵和数组运算

MATLAB的二维数组和矩阵从外观和数据结构上看没有区别。但是，矩阵的运算规则是按线性代数运算法则定义的;而数组运算是按数组的元素逐个进行的。
1．矩阵运算的函数
MATLAB提供了许多矩阵运算的函数，使很多复杂的运算变得很简单。常用矩阵运算函数为：

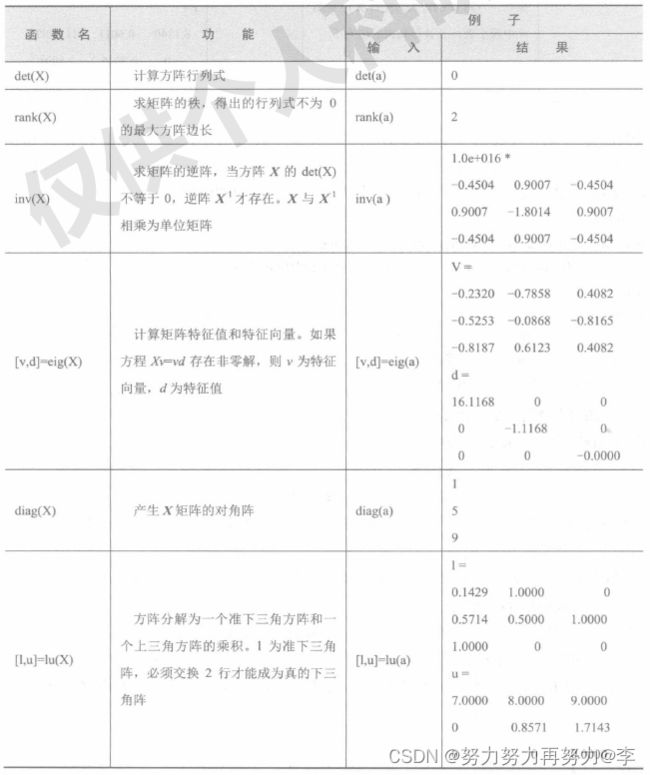
说明:在上表中det(a)=0或det(a)虽不等于0但数值很小，接近于0，则计算inv(a)时，其解的精度比较低，用条件数（求条件数的函数为cond)表示，条件数越大，其解的精度越低，MATLAB会提出警告:“条件数太大，结果可能不准确”。
2.矩阵和数组的算术运算
矩阵和数组的算术运算介绍如下
(1）矩阵和数组的加、减运算。
①矩阵加、减运算表达式分别为“A+B”、“A-B”。
A和B矩阵必须大小相同才可以进行加减运算。如果A、B中有1个是标量，则该标量与矩阵的每个元素进行运算。
数组的加、减法运算规则与矩阵的完全相同，运算符也完全相同。
(2）矩阵和数组的乘法运算。
①矩阵的乘法运算表达式为“A*B”，表示矩阵相乘。
矩阵A的列数必须等于矩阵B的行数，除非其中有1个是标量。
②数组的乘法运算表达式为“A.B(点乘）”，运算符为“.”，表示数组A和B中的对应元素相乘。
A和B数组必须大小相同,除非其中有1个是标量。

(3）矩阵和数组的除法。
(4）矩阵和数组的乘方。

3．矩阵和数组的转置
矩阵和数组的转置介绍如下。
(1）矩阵的转置运算。
“A’ ”表示矩阵A的转置，如果矩阵A为复数矩阵，则为共辄转置。
(2）数组的转置运算。
“A.’ ”表示数组A的转置，如果数组A为复数数组，则不是共辄转置。
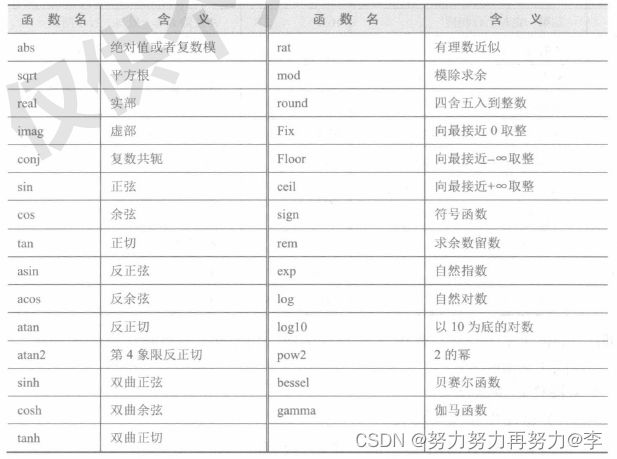
4.矩阵和数组的数学函数
MATLAB中 exp、sqrt、sin、cos等数学函数可以直接在数组上使用，这些运算分别对数组的每个元素进行运算。
下面将矩阵和数组运算进行对比:
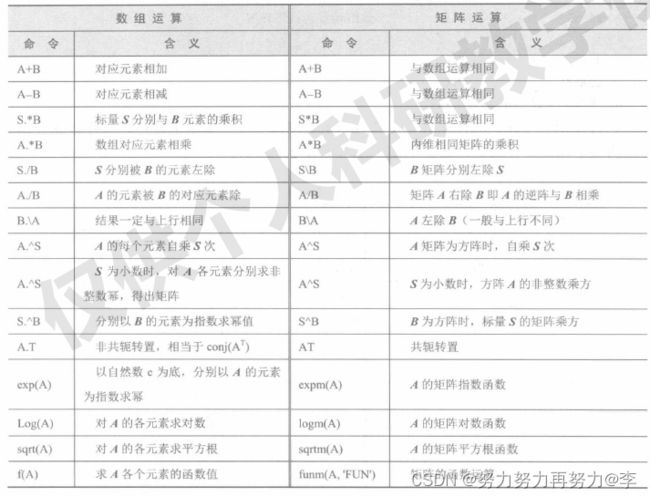说明: funm (A,‘FUN’)要求A必须是方阵，“FUN”为矩阵运算的函数名，如 funm(A,‘sqrt’）等同于sqrtm(A)。

5.关系操作和逻辑操作。
逻辑运算规则如下:
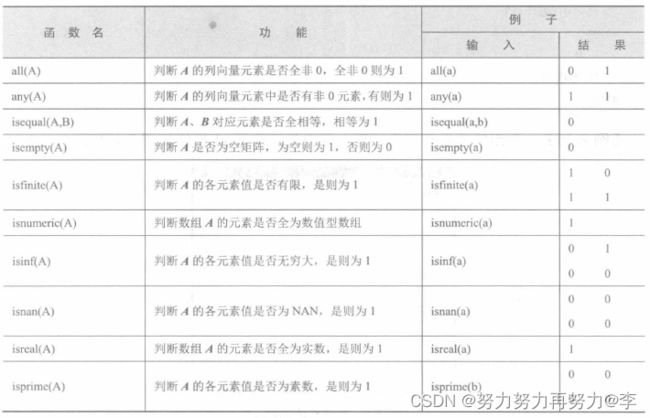
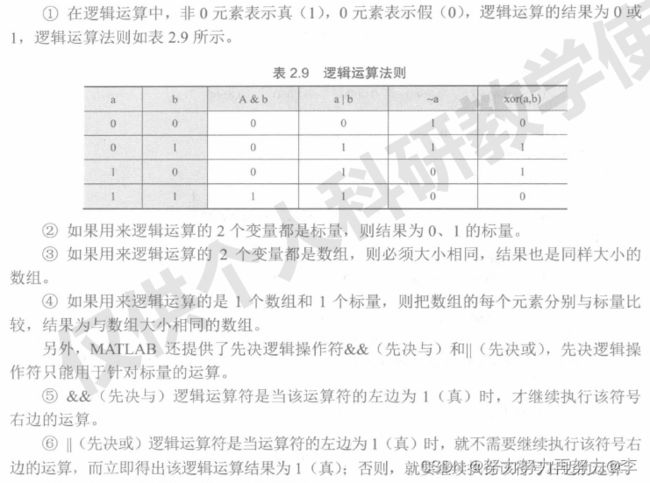(3)函数运算。在MATLAB中能得出真(1）和假（0）结果的函数有:关系逻辑函数、工作状态判断函数、特殊数据判断函数和数据类型函数。常用的关系逻辑函数如下表所示。
6.运算符优先级

7.5多维数组

对于二维数组，人们习惯地把数组的第1维称为行，把第⒉维称为列，则二维数组可以视做“矩形面”。三维数组是二维数组的扩展，用3个下标表示，在二维数组的基础上增加了一维称为页，三维数组可以视做“长方体”。
三维数组的元素存放遵循“单下标”的编号规则:第1页第1列下接该页的第2列，下面再接第3列，依此类推;第1页的最后列接第﹖页第1列，如此进行，直至结束。
四维数组与三维数组可以同样考虑，用4个下标表示。由于更高维数组的形象思维较困难,因此，以下内容主要以三维数组为例。
1.多维数组的创建
创建多维数组方法与创建矩阵的方法相似，最常用的有以下几种。
(1）通过“全下标”元素赋值方式创建。

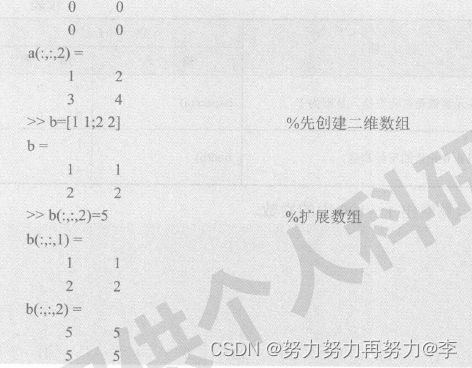
(2)由函数ones、zeros、rand 和 randn直接创建。
(3）利用函数生成数组。
①将一系列数组沿着特定的维连接成1个多维数组。
语法:cat（维,p1,p2,…)
说明:第1个参数“维”是指沿着第几维连接数组p1、p2等。②按指定行列数放置模块数组生成多维数组。
语法:repmat§
repmat（p,行 列 页…)
说明:第1个输入变量p是用来放置的模块数组，后面的变量要放在指定的各维。
③在总元素的数目不变的前提下重新确定数组的行列数来重组数组。
语法:reshape§
reshape （p,行 列 页…)
说明:第1个变量是待重组的数组p，后面的变量是重新生成数组的行数、列数和页数。

2.多维数组的标志
为了能够更好地对多维数组进行操作，MATLAB提供了对多维数组标志的函数。
(1)直接给出数组的维数。
语法:ndims §
(2)给出数组各维的大小。
语法:[m,n,…]=size§ %得出各维的大小
m=size(p,X) %得出某一维的大小
说明: p为需要得出大小的多维数组;m为行数，n为列数…;当只有1个输出变量时，x=1返回第1维（行数)，x=2返回第2维（列数)，依此类推。

(3）返回行数或列数的最大值。语法:
length§
说明:length§等价于max(size§)。

---

总结

本次学习内容：矩阵与数组的输入格式及相应运算，简单介绍了一下多维数组，矩阵与数组相关运算比较复杂，需要仔细理解及学习。需要记背的内容比较多。
文章内容来自MATLAB实用教程/郑阿奇主编，ISBN 978-7-121-29138-8。若有侵权行为，请联系我自行删除。