机器学习-决策树算法代码详注

决策树基本知识：

个人理解：通过数据的各类特征，进行有限次的划分（树型结构），使数据达到快速分类的效果。

优点：计算复杂度不高，结果易于理解

缺点：容易产生过拟合现象，所以需要对决策树进行剪枝

前提知识：熵、信息增益（信息在数据划分之前和之后发生的变化大小，与熵的减小程度成正比，即数据有序程度成正比）：https://blog.csdn.net/hi_sir_destroy/article/details/108812865

构造决策树 “特征” 选取算法、剪枝算法见下博客链接https://www.jianshu.com/p/b7d71478370d

代码例子来源：《机器学习实践》第三章

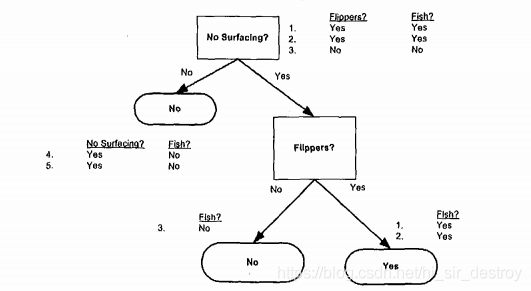
数据包含5个海洋动物，特征包括:不浮出水面是否可以生存，以及是否有脚蹼，将这些动物分成两类:鱼类和非鱼类。

目标：确定依据第一个特征还是第二个特征划分数据。也就是逐渐构造决策树的过程

 当看完前提知识，请再理解下图公式

# -*- coding: UTF-8 -*-
from math import log

# 计算香农熵
def calsShannonEnt(dataSet):
    dataCount = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]  # 数据表中最后一列表示 “结果”
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel]=0
        labelCounts[currentLabel] += 1  # 统计相应类别结果出现的概率
    shannonEnt = 0.0  # 香浓熵
    for key in labelCounts:
        prob = float(labelCounts[key])/dataCount  # 每个结果出现的概率
        shannonEnt -= prob * log(prob,2)  # 计算香农熵 -pi*log(pi)，
    return shannonEnt  # 熵越大，数据越无序

# 创建数据集
def createDataSet():
     dataSet=[[1,1,'yes'],
              [1,1,'yes'],
              [1,0,'no'],
              [0,1,'no'],
              [0,0,'no']]
     labels = ['no surfacing','flipper']
     return dataSet,labels

# 划分数据集 参数：数据集、带分类的特征号、相应特征的值，
# 函数返回数据剩下的特征极其值列表，
# 比如（data,0,0）表示找出0号特征值为0的数据，并返回这些数据的其他特征及其值
def splitData(data,axis,value):
    retdata = []
    for featvec in data:
        if featvec[axis]==value:
            reduceFeatVec = featvec[:axis]
            reduceFeatVec.extend(featvec[axis+1:])
            retdata.append(reduceFeatVec)
    return retdata

# 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
    numFeature = len(dataSet[0])-1  # 获得每个数据的特征数量
    baseEntropy = calsShannonEnt(dataSet)  # 计算数据集的香农熵
    bestInfoGain = 0.0  # 最大信息增益先设为0，接下来是计算出能产生最大信息增益的特征
    bestFeature = -1  # 用于分类最合适的数据特征，先默认为-1
    for i in range(numFeature):  # 该循环用于遍历数据的所有特征
        featList = [example[i] for example in dataSet]  # 找出每一行数据特征标号为i的特征值
        uniqueVals = set(featList)  # 对找到的特征值数据做集合处理。去掉重复值
        newEntropy = 0  # 定义一个新的熵值
        for value in uniqueVals:  # 对集合中“i号特征”的每一个特征值进行处理，是对该“i号特征”所有取值期望的计算
            subDataSet = splitData(dataSet,i,value)  # 得到“i号特征”的特征值为value的数据行，的其他特征的数据列表
            prob = len(subDataSet)/float(len(dataSet))  # 计算出现“该类数据”的概率
            newEntropy += prob*calsShannonEnt(subDataSet)  # 计算“该类数据”的香农熵
        infoGain = baseEntropy - newEntropy  # 计算熵的变化值，infoGain越大，表示新的熵越小，表示通过该特征分类之后，信息增益更大，即无序的减少
        if (infoGain > bestInfoGain): # 找出信息增量最大的“标号特征”
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature



data,labels=createDataSet()
print(splitData(data,0,1))  # 以0号特征，特征值为1的数据进行分类，
print(splitData(data,0,0))  # 以0号特征，特征值为0的数据进行分类，
#print(calsShannonEnt(data))
print(chooseBestFeatureToSplit(data)) # 确定第一个数据划分的依据特征

由于该例子特征只有2个，所以确定一个，就只剩下最后一个特征进行分类了。

 

# 确定最后的分类特征标签
def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    return sortedClassCount[0][0]

# 创建树代码
def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]  # 数据集结果列表
    if classList.count(classList[0]) == len(classList):  # 类别完全相同，则停止划分
        return classList[0]
    if len(dataSet[0]) == 1:  # 只剩下结果集，表示分类完成，返回分类列表
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)  # 特征选择函数
    bestFeatLabel = labels[bestFeat]  # 相应特征的语言描述
    myTree = {bestFeatLabel:{}}  # 创建树
    del(labels[bestFeat])  # 删除已经用过的特征描述
    featValues = [example[bestFeat] for example in dataSet]  # 获取该特征的取值情况
    uniqueVals = set(featValues)  # 对取值进行去重
    for value in uniqueVals:
        sublabels = labels[:]  # 构造剩下的特征数据
        myTree[bestFeatLabel][value] = createTree(splitData(dataSet,bestFeat,value),sublabels)  # 递归造树
    return myTree