ML(4) - LinearRegression多项式回归(非线性)

---

多项式回归基本概念

• 对于线性回归，数据都是线性的，目标是寻找一条直线，尽可能的拟合样本。但实际任务中，数据往往是非线性，因此需对线性回归算法进行一些转换改造，即多项式回归。
  
• 多项式回归中，数据不太具有线性关系，因此应寻找一些非线性曲线去拟合。如下图，用一条二次曲线去拟合数据，效果更好。
  
• 对于上面的数据，原本是只有x一个特征，但是我们可以构造一个新的特征$x^2$，即构成了二次函数。将二次函数看成$y=a{x}_1+bx+c$ 其中($x_1=x^2$)。这样就又变成解多元线性回归的问题了。

Scikit-Learn中多项式回归

• scikit-learn 中并没有直接封装多项式回归。
• 通过使用 sklearn.preprocessing.PolynomialFeatures 改变样本幂次，构造新特征，再调用线性回归来实现多项式回归。

import numpy as np 
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression

# 构造模拟数据，X特征(一维) , y真值
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)

# 创建对象并填入将样本改成 最高degree次幂
poly = PolynomialFeatures(degree=2)
#fit原样本
poly.fit(X) 
#修改原样本，构造新特征。
X2 = poly.transform(X) 
>>>X2[:5,:]
>>>'''第一例是x0特征，第二列原样本，第三列原样本2次幂样本'''
	array([[ 1.        ,  0.14960154,  0.02238062],
   	      [ 1.        ,  0.49319423,  0.24324055],
          [ 1.        , -0.87176575,  0.75997552],
          [ 1.        , -1.33024477,  1.76955114],
          [ 1.        ,  0.47383199,  0.22451675]])

# 调用线性回归模型
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)
plt.scatter(x, y)
#np.sort排序，np.argsort排序索引
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')

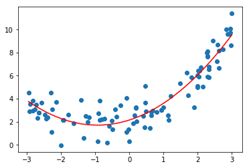
'''创建模拟数据使用的方程 y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)'''
>>>lin_reg2.coef_
'''得到系数与原方程1和0.5相当接近'''
array([ 0.        ,  0.9460157 ,  0.50420543])
'''得到截距与原方程2相当接近'''
>>>lin_reg2.intercept_
2.1536054095953823

关于PolynomialFeatures

• 对于原样本不只一个特征时，PolynomialFeatures 构造新样本特征采用如下规则：

X = np.arange(1, 11).reshape(-1, 2)
>>> X.shape
	(5,2)
>>> X
	array([[ 1,  2],
      	   [ 3,  4],
           [ 5,  6],
           [ 7,  8],
           [ 9, 10]])
           
poly = PolynomialFeatures(degree=2)
poly.fit(X)
X2 = poly.transform(X)
>>> X2.shape
	(5, 6)
>>> X2
	array([[   1.,    1.,    2.,    1.,    2.,    4.],
    	   [   1.,    3.,    4.,    9.,   12.,   16.],
      	   [   1.,    5.,    6.,   25.,   30.,   36.],
       	   [   1.,    7.,    8.,   49.,   56.,   64.],
           [   1.,    9.,   10.,   81.,   90.,  100.]])
''' 第1例x0特征，第2、3列原样本，第4、6列原样本2次幂,第5列两个原样本乘积
	x1 ,x2 --> 1, x1, x2, x1^2, x1x2, x2^2
'''

• 当PolynomialFeatures(degree=3)时，有10项：