【机器学习小论文】sklearn线性回归LinearRegression代码及调参

一、前言

最近在写小论文，就是硕士毕业论文的部分成果，需要用到线性回归，所以就把相关代码贴上，便于日后写论文时总结，也顺便给后来者提供思路。小论文的思路主要是，先用线性回归，再用随机森林，最后再用xgboost，来预测房价，最后得出结论。所以，这个会陆续的贴出相关代码。至于数据清洗那一块，暂时不贴上了，主要原因就是数据清洗不容易，并且每个人的清洗方法也不一样，所以主要还是看思路。

二、算法简介

2.1 什么是回归分析

回归分析是一种预测性的建模技术，它研究的是因变量（目标）和自变量（预测器）之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。通常使用曲线/线来拟合数据点，目标是使曲线到数据点的距离差异最小。股票预测，房价预测等都属于回归分析，简单理解即：预测结果可以是任意的。和分类分析对比，分类就是对与错，1和0，是与否的关系，而回归问题则是结果不固定，可能是一个区间内的任意数字，比如房价，比如工资，可能是1-1w内的任意数字。

2.2 线性回归

线性回归是回归问题中的一种，线性回归假设目标值与特征之间线性相关，即满足一个多元一次方程。通过构建损失函数，来求解损失函数最小时的参数w和b。通长我们可以表达成如下公式：

y^为预测值，自变量x和因变量y是已知的，而我们想实现的是预测新增一个x，其对应的y是多少。因此，为了构建这个函数关系，目标是通过已知数据点，求解线性模型中w和b两个参数。

如果预测的是房价，最简单的理解，面积*单价=总价，但是单价是怎么来的呢？为啥有的地方可以卖到1w，有些地方能卖到3w呢，所以说房价的影响是多因素的。那么用线性回归来预测房价，只能说太过理想化或者简单化了。预测的结果肯定不会太高。

2.3 目标/损失函数

求解最佳参数，需要一个标准来对结果进行衡量，为此我们需要定量化一个目标函数式，使得计算机可以在求解过程中不断地优化。

针对任何模型求解问题，都是最终都是可以得到一组预测值y^ ，对比已有的真实值 y ，数据行数为 n ，可以将损失函数定义如下：

即预测值与真实值之间的平均的平方距离，统计中一般称其为MAE(mean square error)均方误差。把之前的函数式代入损失函数，并且将需要求解的参数w和b看做是函数L的自变量，可得

现在的任务是求解最小化L时w和b的值，

即核心目标优化式为

求解方式有两种：

1）最小二乘法(least square method)

求解 w 和 b 是使损失函数最小化的过程，在统计中，称为线性回归模型的最小二乘“参数估计”(parameter estimation)。我们可以将 L(w,b) 分别对 w 和 b 求导，得到

令上述两式为0，可得到 w 和 b 最优解的闭式(closed-form)解：

 

2）梯度下降(gradient descent)

梯度下降核心内容是对自变量进行不断的更新（针对w和b求偏导），使得目标函数不断逼近最小值的过程

这里不做展开讲解。

三、代码及结果分析

from sklearn.impute import SimpleImputer
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import KFold
from sklearn.metrics import r2_score
from sklearn.preprocessing import *
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import importlib
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import metrics
# 因为plt画图需要字体，所以下列三行是设置字体
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False

df_merge = pd.read_csv('D:/myCode/spark/spark_ML/df_merge.csv')

#用常数填充
df_merge = df_merge.replace(np.nan, 0)

# ****************线性回归***************************************************8
from sklearn.linear_model import LinearRegression
# 准备训练、测试集
X = df_merge.drop(['成交价'],axis=1)
y = df_merge['成交价']
x_train,x_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=42)    # random_state=42
x_train = x_train.astype(np.float64)
x_test = x_test.astype(np.float64)

# print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)

# 设定回归算法
lr = LinearRegression()
# 使用训练数据进行参数求解
lr.fit(x_train, y_train)
# LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
# print('求解系数为：', lr.intercept_)
# print('求解系数为：', lr.coef_)

# 对测试集的预测
y_hat = lr.predict(x_test)
# 打印前10个预测值
print("*"*10)
print("真实值：")
print(y_test[0:20])
print("预测值：")
print(y_hat[0:20])
# y_hat[0:9]
print("*"*10)

# y_test与y_hat的可视化
# 设置图片尺寸
plt.figure(figsize=(10, 6))
# 创建t变量
t = np.arange(len(x_test))
# 绘制y_test曲线
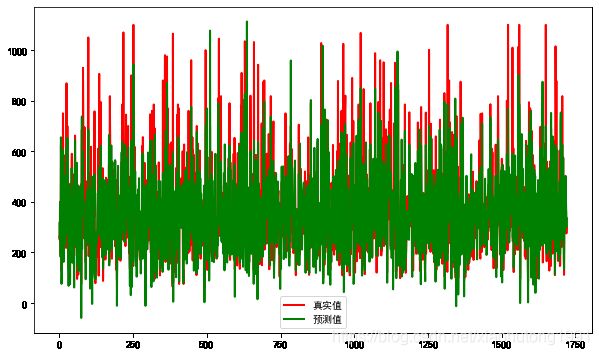
plt.plot(t, y_test, 'r', linewidth=2, label='真实值')
# 绘制y_hat曲线
plt.plot(t, y_hat, 'g', linewidth=2, label='预测值')
# 设置图例
plt.legend()
plt.show()

# 拟合优度R2的输出方法
print("r2:", lr.score(x_test, y_test))

# 用Scikit_learn计算MAE
print("MAE:", metrics.mean_absolute_error(y_test, y_hat))

# 用Scikit_learn计算MSE
print("MSE:", metrics.mean_squared_error(y_test, y_hat))

# 用Scikit_learn计算RMSE
print("RMSE:", np.sqrt(metrics.mean_squared_error(y_test, y_hat)))

结果

r2: 0.7374872620731299
MAE: 65.10673914738442
MSE: 8829.098955225081
RMSE: 93.96328514491753

运行时间： 0:00:00.299199 秒

 调参：

LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None)
fit_intercept:是否有截据，如果没有则直线过原点;
normalize:是否将数据归一化;
copy_X:默认为True，当为True时，X会被copied,否则X将会被覆写;
n_jobs:默认值为1。计算时使用的核数

分析：r2: 0.7374872620731299的值不算高，MSE: 8829.098955225081是挺高的，说明和预测值差距比较大。从图中也看出，好多的预测值偏低。毕竟线性回归本来就是毕竟简单的模型，也没有进行调参，那结果肯定可想而知。就像一个学生只知道学习，还是那种死学习，那他的成绩肯定高不到哪里去。下边的是预测值和真实值的比较。数据集大概是8k左右。有些还是比较准的，有些感觉就是瞎扯了。O(∩_∩)O哈哈~

    预测值      真实值
 261.6408733    260
320.36511994    249
259.65389878    400
393.58315287    341
181.33705676    189
655.13792816    623
405.27933678    505
 75.46051886    126
138.83768312    245
275.73318861    209
329.22648801    295
248.37913372    356
606.88028161    750
  432.380307    400
162.20349804    177
453.66704175    344
299.03437647    216
285.30563981    284
228.46034506    245
271.25327428    345