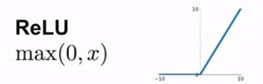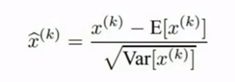【CS231n 学习笔记】Lecture5:Training Neural Networks Part 1
CS231n学习笔记目录(2016年Andrej Karpathy主讲课程)
- Lecture1:Introduction(介绍)
- Lecture2:Image Classification Pipeline(数据驱动的图像分类方式) (上)
- Lecture2:Image Classification Pipeline(数据驱动的图像分类方式) (下)
- Lecture3:Loss functions and Optimization(线性分类器损失函数与最优化)
- Lecture4:Backpropagation and Neural Networks(反向传播与神经网络)
- Lecture5:Training Neural Networks(神经网络训练细节) Part 1
- Lecture6:Training Neural Networks(神经网络训练细节) Part 2
- Lecture7:Convolutional Neural Networks(卷积神经网络)
-
Lecture8:Spatial Localization and Detection(迁移学习之物体定位与检测)
Some wrong views
错误观点:ConvNets need a lot of data to train
事实上对于设计目的来说这是一个错误的观点,完全可以使用小数据集来训练,原因是我们可以通过一些细调来得到更多的细节。
大多数情况下我们不会一开始就进行卷积网络的训练,通常会先进行预训练和细调,先在一些大的训练集上(如ImageNet数据集)进行训练,再将训练的结果转移到自己的小数据集中。而ImageNet的预训练已经有人做好了,很多人用了数月的时间对卷积神经网络在不同的数据集上进行测试,并将训练好的模型上传到caffe model zoo,这些模型中大量的超参数已经设置好了,所以我们只需要用自己的数据集去训练,然后进行调整。
错误观点:We have infinite compute available because Terminal
有人认为计算机的运算能力是无限的,但实际上训练大数据集需要很长的时间,我们并没有那么多的GPU,还需要进行很多超参数的优化,因此计算机存在很多性能上的约束。
History of Neural Networks
第一个神经网络的提出大约在1957年,Frank Rosenblatt 设计了一个被称作感知机的机器,无法像现在这样编码,而是通过电路和电子元件连接,并提出了学习法则,通过设置权值来使得感知机得到的结果与所期望的结果相匹配,但并没有提出损失函数、反向传播的概念。
后来人们开始改进它,在1960年,Widrow and Hoff制造出了适应性(Adaline/Madaline)神经元,他们将这些感知机整合成了一个多层次的感知机网络,同样也是由电路和电子元件组成的,也没有反向传播的概念,都是通过制定一些学习法则观察性能改变的变化情况,人们认为这个机器有着很好的前景,这时程序设计的概念已经体现的很明显了,人们第一次想到这种数据驱动的方法,使得机器有了学些能力,这是一个巨大的概念性的飞跃,但这个机器的工作性能并不理想。
在20世纪70年代,神经网络领域几乎没有进展,也没有多少相关的研究。大概在1986年,神经网络再次有了一个突破性的进展,Rumelhart 的论文第一次用清晰的公式很好地阐述了反向传播的概念。他们摈弃了学习法则的思想,提出了损失函数的公式,讨论了反向传播、梯度下降等问题,但不幸的是,当他们将神经网络设计的更深时,工作效果并没有机器学习的一些算法好,因此他们的网络训练遇到了阻碍,反向传播效果也不太好,尤其是在训练大规模神经网络的情况下。由于这些阻碍,在大概近20年的时间里都很少有相关的研究。
2006年,这项研究再次得到了复兴,在Hinton and Salakhutdinov发表的论文中,第一次建立了神经网络的模型,他们采用了一个无监督预训练的方案,使用了RBM(限制玻尔兹曼机),而不是在单通道中对所有层都经过反向传播,这相当于在训练第一层时使用了一个无监督的目标,在此之上训练下面的层,当训练完成将它们整合起来,然后进行反向传播并调节参数。
在2010年,神经网络领域有了一个非常大的成果,与机器学习的其他算法相比效果更好,尤其是在语音识别方面。2012年,在计算机视觉的图像识别领域提出了AlexNet,人们开始关注神经网络,这一领域的发展也越来越迅速。
Activation Functions
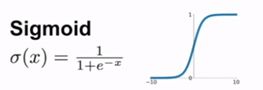
Sigmoid
Sigmoid函数是一个挤压函数,取值为[0,1]之间的实数:
缺点:
一个饱和的神经元的输出要么非常接近于0,要么非常接近于1,这些神经元会导致在反向传播算法中出现梯度趋于0的问题(梯度消失问题)。
其次,sigmoid函数的输出不是关于原点中心对称的,因此收敛的效果可能不太好。
和另外的一些函数相比,sigmoid函数中关于x的计算是很耗时的,当训练大规模卷积网络时,需要花费很多计算时间。
tanh
sigmoid函数不是关于原点对称的,有人在1991年写了一篇关于如何优化网络的论文,推荐使用tanh函数来代替sigmoid函数。Tanh函数就相当于将两个sigmoid函数叠加在一起,最终得到的输出位于[-1,1]之间。
缺点:
依然存在梯度消失的问题、计算依然很耗时。
ReLU
在2021年左右,在一篇关于卷积神经网络的论文中提出了这种非线性函数max(0,x),可以是网络收敛速度更快。因为至少在输入x为正时函数不会饱和,梯度不会趋于0,在这一区域不会出现梯度消失问题,而且计算效率很高,从实验结果来看该函数的收敛速度更快。
缺点:
ReLU函数也不是关于原点中心对称的。
在反向传播中,当输入x小于0时,ReLU函数就会一直处于未激活状态,就会出现梯度消失问题。
在实际训练中,如果神经元的输入为负,那么ReLU就不会被激活(dead ReLU),梯度就会一直为0,不会再对任何数据有所作用,参数永远不会被更新,产生这种情况的原因一般有两种:
一种是在初始化过程中,不幸地将权重设置为不能激活神经元的数值;
更常见的情况是在训练的过程中学习率设置的太高,可能会发生数据多样性的丢失,且不可逆转。因此人们通常把偏置值设置成很小的正数(如0.01),而不是0,因为这会使得未经初始化的ReLU更多的输出正值,使参数得到更新。
Leaky ReLU
Leaky ReLU是基于ReLU函数的修正,将负值部分的斜率变成0.1而不是0,能够解决dead ReLU问题。0.1这个值实际上可以是任意的参数。
ELU
前不久人们提出了一种新的激活函数,叫做指数线性单元(ELU),它继承了ReLU函数的所有优点,并且近似零中心化。
Maxout单元
它不仅仅是W转置乘以x的函数,而且有两组权重,计算得到两个超平面,然后取最大值。不会出现神经元失活问题,是分段线性的,效率较高。
缺点:
两倍参数的问题,使用的并不普遍。
Data Preprocessing
在机器学习中通常会对数据进行归一化处理,确保每个维度的值都位于特定区间内,但在图像处理中并不常用,因为图像数据中的所有特征都是像素,取值均在0到255之间,所以归一化并不常用,在图像处理中常用的是mean centery及其变种。
Weight Initialization
首先考虑如果不进行权重初始化会怎样?特别的,将所有权重都设为0,那么每一层的神经元学到的东西都是一样的,反向传播计算的梯度也都一样,参数更新也都一样,因此该方式不好。
因此第一种方法是给定很小的随机数来初始化权重,比如从标准差0.01的高斯分布中随机抽取,但这种方法在层数很多的神经网络表现不好。W的梯度等于x乘以上层梯度,如果x是小量,那么W的梯度也是小量,在反向传播的过程中每一层会不断乘以W,这样最终的数据就会趋于0,得到的梯度也会非常小,就会产生梯度消失的问题。如果将标准差改为1,那么就会出现另一个问题,由于数据过于饱和使得梯度越来越大,就会产生梯度爆炸的问题,
Batch Normalization
批量归一化是最近才提出的方法,目的是希望神经网络的每一部分都有粗略的单位高斯激活(roughly unit gaussian activation):
该方法接收输入x,计算出每一个特征的经验均值E和方差Var,保证这批数据的每一个特征维度都有单位高斯激活。通常我们会在一个全连接层(fully connected)或者卷积层(convolutional layers)后面接上批量归一化层(batch normalization)。
BN层将单位高斯激活后的结果输入到tanh函数,但tanh是否一定想要这样的输入呢?在tanh中我们希望避免饱和,但也许有一点点饱和也并不是坏事,因此我们可以通过控制饱和的程度,来决定输入到tanh中的数据格式。这就是批量归一化的另一部分,在规范化之后可以对x的每一个输入特征进行移动,通过乘以γ再加上β,它使得神经网络在得到单位高斯激活值之后依然可以根据需要改变数值。特别的,当γ和β分别取值方差和均值时,神经网络就相当于抵消了BN的效果,因此BN其实等价于一个恒等函数,或者说可以通过学习达到恒等的作用。
优点:
BN算法增强了整个神经网络的梯度流;
支持更高的学习率,可以更快地训练模型;
它减少了算法对合理初始化的依赖。当改变初始值域的大小时,有无BN会产生很大的区别,使用BN时会发现算法适用于更多的初始值,所以在初始化的时候不用考虑太多。
BN实际上起到了一些正则化的作用,且减少了dropout的需要(后面会讲)。
Babysitting the Learning Process
实验过程中可以先去一小部分数据集测试神经网络的完整性,忽略掉正则化,测试神经网络在这小部分数据集上是否能够达到过拟合,如果达到过拟合,就说明反向传播、参数更新正常,接下来就可以扩大数据集,通过实验来找出合适的学习率。
Hyperparameter Optimization
超参数优化使用从粗糙到精细化的思想,首先只需要确定一个大概的参数区间,然后逐渐寻找较好的学习率区间,一遍遍地重复该过程,让选择的区间越来越窄,最后选出一个表现最好的参数。
(纯学习分享,如有侵权,联系删文)