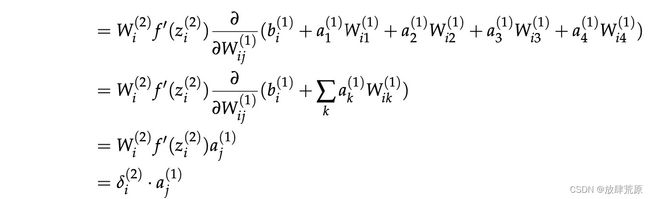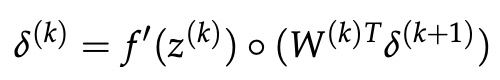CS224n: Natural Language Processing with Deep Learning 笔记、文献及知识点整理(六)神经网络、反向传播(二)
关键词:神经网络 Neural networks、正向计算 Forward computation、反向传播 Backward propagation、神经元 Neuron Units、最大边际损失 Max-margin Loss、梯度检查 Gradient checks、Xavier参数初始化 、学习率 Learning rates、Adagrad。
讲义:神经网络、反向传播 (Lecture Notes: Neural Networks, Backpropagation)
课程讲师:Christopher Manning、Richard Socher
讲义作者:Rohit Mundra、Amani Peddada、Richard Socher、Qiaojing Yan
1 神经网络:基础(Neural Networks: Foundations)
本文上一部分请见:CS224n: Natural Language Processing with Deep Learning 笔记、文献及知识点整理(六)神经网络、反向传播(一)_放肆荒原的博客-CSDN博客
1.5 反向传播训练——基本
在本节中,我们将讨论当 1.4 节中讨论的成本 J 为正时如何训练模型中的不同参数。 如果成本为 0,则不需要更新参数。 由于我们通常使用梯度下降(或 SGD 等变体)更新参数,因此我们通常需要根据更新方程的需要,获取参数的梯度信息:
反向传播是一种技术,允许我们使用微分链规则计算模型前馈计算中使用的任何参数的损失梯度。为了进一步理解这一点,我们来看看图5所示的玩具网络,我们将对其执行反向传播。
图 5:这是一个 4-2-1 神经网络,其中第 k 层的神经元 j 接收输入 并产生激活输出
并产生激活输出 ![]() 。
。
在这里,我们使用具有单个隐藏层和单个单元输出的神经网络。 我们先建立一些符号,以便以后更容易地推进这个模型:
• ![]() 是神经网络的输入。
是神经网络的输入。
• s 是神经网络的输出。
• 每层(包括输入层和输出层)都有接收输入并产生输出的神经元。 第 k 层的第 j 个神经元接收标量输入  并产生标量激活输出
并产生标量激活输出 ![]() 。
。
• 我们把在  处计算的反向传播误差称为
处计算的反向传播误差称为  。
。
• 第1 层是指输入层,而不是第一个隐藏层。 对于输入层, 。
。
•  是将第k 层的输出映射到第(k+1) 层的输入的传递矩阵。因此,
是将第k 层的输出映射到第(k+1) 层的输入的传递矩阵。因此,![]() 和
和 要使用来自第 1.3 节的符号。
要使用来自第 1.3 节的符号。
我们开始:假设成本 是正的,并且我们想要执行参数
是正的,并且我们想要执行参数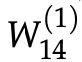 的更新(在图5和图6中),我们必须认识到
的更新(在图5和图6中),我们必须认识到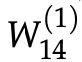 只对
只对 起作用,从而对
起作用,从而对 起作用。这一事实对于理解反向传播至关重要–反向传播的梯度仅受其贡献的值的影响。因此,
起作用。这一事实对于理解反向传播至关重要–反向传播的梯度仅受其贡献的值的影响。因此, 用于与
用于与 相乘的分数正向计算。我们可以从最大边际损失中看出:
相乘的分数正向计算。我们可以从最大边际损失中看出:
我们在上面看到,梯度降低到乘积 ,其中
,其中 本质上是从第2层的第i个神经元向后传播的误差。
本质上是从第2层的第i个神经元向后传播的误差。 是由Wij缩放时馈送至第2层第i个神经元的输入。
是由Wij缩放时馈送至第2层第i个神经元的输入。
我们以图6为例更好地讨论反向传播的“错误共享/分布”解释。假设我们要更新 :
:
2. 然后,我们将这个误差乘以神经元的局部梯度,该梯度将 映射到
映射到 。在这种情况下,这恰好是1,因此,误差仍然是1。现在称为
。在这种情况下,这恰好是1,因此,误差仍然是1。现在称为 =1。
=1。
3. 此时,误差信号1已达到 。我们现在需要1来分配误差信号,以便误差的“公平份额”达到
。我们现在需要1来分配误差信号,以便误差的“公平份额”达到 。
。
5. 正如在第 2 步中所做的,我们需要移动误差到将 映射到
映射到 的神经元上。 我们通过将
的神经元上。 我们通过将  处的误差信号乘以神经元的局部梯度
处的误差信号乘以神经元的局部梯度 来实现。
来实现。
7. 最后,我们需要将错误的“公平份额”分配给  ,只需将其乘以它负责转发的输入,恰好是
,只需将其乘以它负责转发的输入,恰好是  。
。
请注意,我们使用这种方法得到的结果与前面使用显式微分得到的结果完全相同。因此,我们可以使用微分链规则或使用错误共享和分布流方法计算网络中某个参数的错误梯度——这两种方法恰好做了相同的事情,但从不同方向上思考会有所帮助。
偏差更新:只要转发的输入为1,偏差项(如 )在数学上等同于对神经元输入(
)在数学上等同于对神经元输入( )有贡献的其他权重。因此,层k上神经元i的偏置梯度为
)有贡献的其他权重。因此,层k上神经元i的偏置梯度为 。例如,如果我们更新
。例如,如果我们更新 而不是上面的
而不是上面的 ,那么梯度就是
,那么梯度就是
 。
。
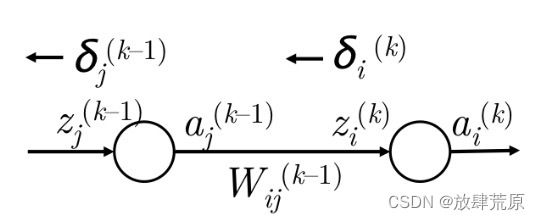
1. 我们有误差 从
从 向后传播,即第 k 层的神经元 i。 参见图 7。
向后传播,即第 k 层的神经元 i。 参见图 7。
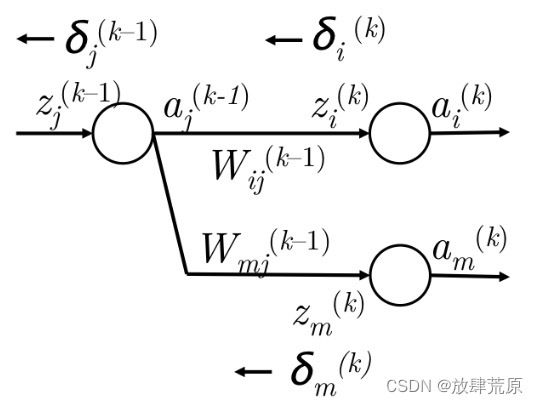
4. 然而,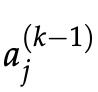 可能已经被转发到下一层中的多个节点,如图 8 所示。它也应该负责使用完全相同的机制从第 k 层的节点 m 向后传播误差。
可能已经被转发到下一层中的多个节点,如图 8 所示。它也应该负责使用完全相同的机制从第 k 层的节点 m 向后传播误差。
7. 现在我们在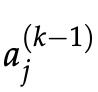 处有正确的错误,我们通过乘以局部梯度
处有正确的错误,我们通过乘以局部梯度 将其移动到第 k-1 层的神经元 j 上。
将其移动到第 k-1 层的神经元 j 上。
1.6 反向传播训练——向量化
到目前为止,我们讨论了如何计算模型中给定参数的梯度。我们将推广上述方法,以便一次性更新权重矩阵和偏差向量。注意,这些只是上述模型的扩展,将有助于在矩阵向量级别建立误差传播方式的直觉。
对于给定的参数 ,我们确定误差梯度只是
,我们确定误差梯度只是 。 提醒一下,
。 提醒一下, 是将
是将 映射到
映射到  的矩阵。 因此,我们可以确定整个矩阵
的矩阵。 因此,我们可以确定整个矩阵 的误差梯度为:
的误差梯度为:
因此,我们可以使用传播到矩阵中的误差向量的外积和矩阵转发的激活来编写整个矩阵梯度。
现在,我们将看到如何计算误差向量![]() 。我们之前用图 8 建立了
。我们之前用图 8 建立了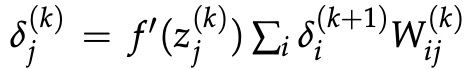 。 这可以很容易地推广到矩阵,使得:
。 这可以很容易地推广到矩阵,使得:
当然,这假设在正向传播中,信号 首先经过激活神经元f产生激活
首先经过激活神经元f产生激活 ,然后通过传递矩阵
,然后通过传递矩阵 线性组合产生
线性组合产生 。
。
计算效率:在探索了元素级更新和向量级更新之后,我们必须认识到,向量化实现在科学计算环境,如MATLAB或Python(使用NumPy/SciPy软件包)中运行得更快。因此,我们应该在实践中使用向量化实现。此外,我们还应该减少反向传播中的冗余计算——例如,注意 是直接取决于
是直接取决于  的。 因此,我们应该确保当我们使用
的。 因此,我们应该确保当我们使用 更新
更新 时,我们要保存
时,我们要保存 以便稍后推导出
以便稍后推导出  ,然后我们对 (k − 1) . . . (1) 重复此操作。 这种递归过程使反向传播成为计算上负担得起的过程。
,然后我们对 (k − 1) . . . (1) 重复此操作。 这种递归过程使反向传播成为计算上负担得起的过程。
<未完待续,下一节《2 神经网络:提示和技巧》>