图像处理——图像傅里叶变换实例

傅里叶变换Fourier Transform，有连续傅里叶变换CFT和离散傅里叶变换DFT，但是用到实时的图像处理中的是快速傅里叶变换。快速傅里叶变换Fast Fourier Transform是DFT的一种算法，但是在运算中减少了大量工作量，所以能够提高运算速度。傅里叶变换在图像分析、图像增强、图像压缩等工作中都有应用。

1.对于已知图像，求其幅值谱和相位谱，并对幅值谱和相位谱分别进行图像重构：

%————1.对已知图像求幅值谱和相位谱，并进行图像重构——————
I=imread('11.png');
% I=rgb2gray(I);
figure,imshow(real(I));
I=I(:, :, 3);

f1=fft2(I);
f2=fftshift(f1);
RRdp1=real(f2); IIdp1=imag(f2);
a=sqrt(RRdp1.^2+IIdp1.^2);
a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;
figure,imshow(real(a));title("幅值谱");

b=angle(f1);
figure,imshow(real(b));title("相位谱");

theta=30;
RR1=a*cos(theta);II1=a*sin(theta);
f11=RR1+i.*II1;
c=ifft2(f11)*255;
figure,imshow(real(c));title("幅值谱重构图像");

m=150;
RR2=m*cos(angle(f1));
II2=m*sin(angle(f1));
f22=RR2+i*II2;
D=ifft2(f22);
figure,imshow(real(D));title("相位谱重构图像");

结果：

分析：
从图中看出，从幅值谱图中得到更多的信息，但是相位谱图像重构后可以基本看出原图像轮廓。

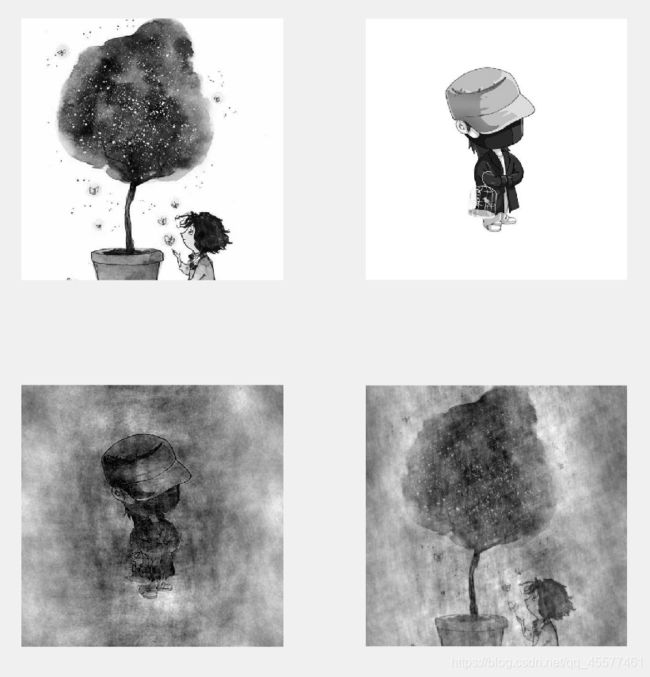
2.对二幅图像分别求幅值谱和相位谱，将相位谱交换，观察结果

% ————2.对已知两幅图像，求其幅值谱和相位谱，并交换两幅图像的相位谱，重构图像————
I=imread('10.jpg');
J=imread('11.png');
[I,J]=CropImage(I,J);
I=rgb2gray(I);
J=rgb2gray(J);
IF=fft2(I); JF=fft2(J);      
% 分别求幅度谱和相位谱
FAI=abs(IF); FPI=angle(IF);     
FAJ=abs(JF); FPJ=angle(JF);
% 交换相位谱并重建复数矩阵
IR=FAI.*cos(FPJ)+FAI.*sin(FPJ).*i;
JR=FAJ.*cos(FPI)+FAJ.*sin(FPI).*i;
IR1=abs(ifft2(IR));
JR1=abs(ifft2(JR));
subplot(2,2,1);imshow(I);
subplot(2,2,2);imshow(J);
subplot(2,2,3);imshow(IR1,[]);
subplot(2,2,4);imshow(JR1,[]);

结果：

实验中要求两幅图像的大小相同，所以我自己做了一个裁剪图像的函数，这个函数把尺寸较大的图像保留较为中心的部分：

function [cropI,cropJ]=CropImage(I,J)

[m1,n1,~]=size(I);
[m2,n2,~]=size(J);

m=min(m1,m2);
n=min(n1,n2);
cropI=zeros(m,n,3);
cropJ=zeros(m,n,3);

if m1<m2
    m=floor((m2-m1)/2);
    if n1<n2
        n=floor((n2-n1)/2);
        cropI=I;
        for i=1:m1
            cropJ(i, :, :)=J(i+m, n:n+n1-1, :);
        end
    else
        n=floor((n1-n2)/2);
        for i=1:m1
            cropI(i, :, :)=I(i, n:n+n2-1, :);
            cropJ(i, :, :)=J(i+m, :, :);
        end
    end
else
    m=floor((m1-m2)/2);
    if n1<n2
        n=floor((n2-n1)/2);
        for i=1:m2
            cropI(i, :, :)=I(i+m, :, :);
            cropJ(i, :, :)=J(i, n:n+n1-1, :);
        end
    else 
        n=floor((n1-n2)/2);
        cropJ=J;
        for i=1:m2
            cropI(i, :, :)=I(i+m, n:n+n2-1, :);
        end
    end
end
cropI=uint8(cropI);
cropJ=uint8(cropJ);