计算机视觉（本科课程） 北京邮电大学 鲁鹏
计算机视觉 2020 北京邮电大学本科课程
这里的计算机视觉中的数学都是比较简单的，不如图形学
课程部分内容
- 计算机视觉 2020 北京邮电大学本科课程
-
- 1. 卷积与边缘提取
-
- 锐化
- 边缘检测
- 2. 拟合
-
- 最小二乘
- Robust estimator
- RANSAC
- Hough
- Model selection
- 3. Harris 角点
- 4.尺度不变区域与SIFT特征
-
- LoG算子 Laplacian of Gaussian
- SIFT 特征
1. 卷积与边缘提取
卷积的padding方式：
clip filter （black）
wrap around
copy edge
reflect across edge
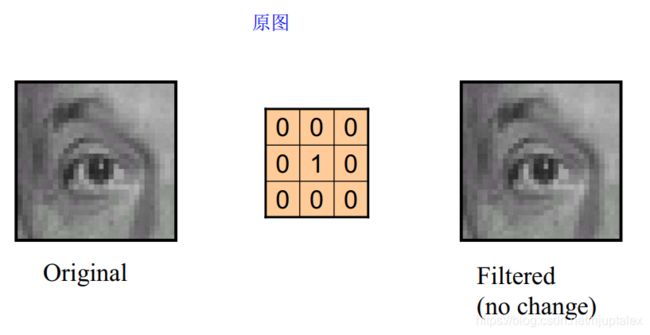
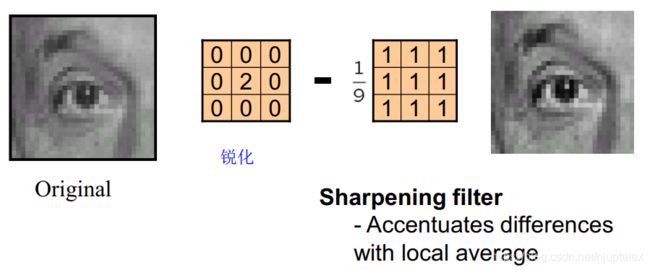
锐化
原图-平滑图=边缘图
原图+边缘图=锐化图
I * e - I * g = detail
I * e + I*(e-g) = sharpened = I * (2e-g)
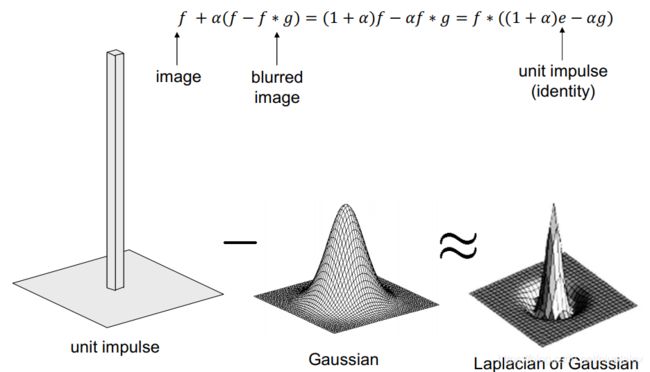
detail前方再加一个参数alpha，调节锐化度，最终约等于对原图乘一个拉普拉斯高斯分布
不用全1的方形滤波，改成圆形的高斯核（中心大四周小）
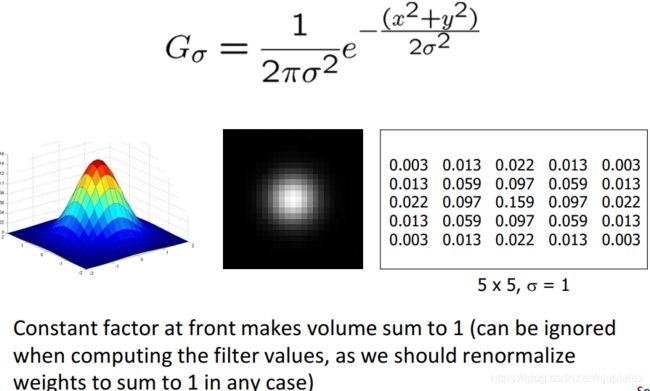
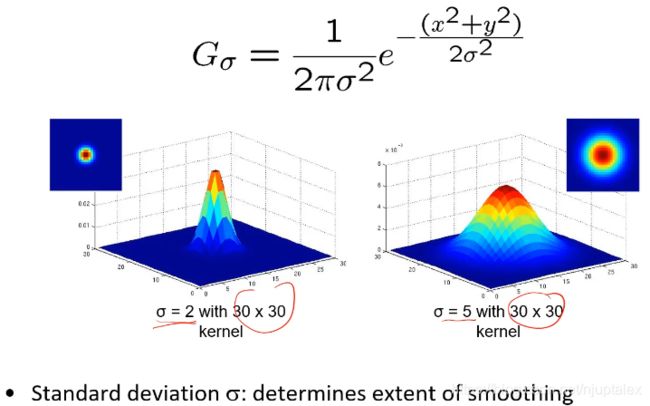
为了让滤波器核有意义，覆盖更多的有值区域，3sigma法则，3倍方差的区域能包含99%的值；so：卷积核的一半长度设置为三倍方差，标准正太sigam=1时，核为7*7
高斯核作用：滤除高频；对一个图像连续高斯两次==一次更大的高斯核卷积
降低卷积运算的复杂度：1）可分离的高斯核：G(x,y) = G(x) * G(y) ；2）两次小卷积代替大卷积
高斯滤波去除高斯噪声，中值滤波（非线性：排序选中止代替周围像素）去除椒盐噪声
边缘检测
确定那些是噪声边，更应该关注什么语义信息
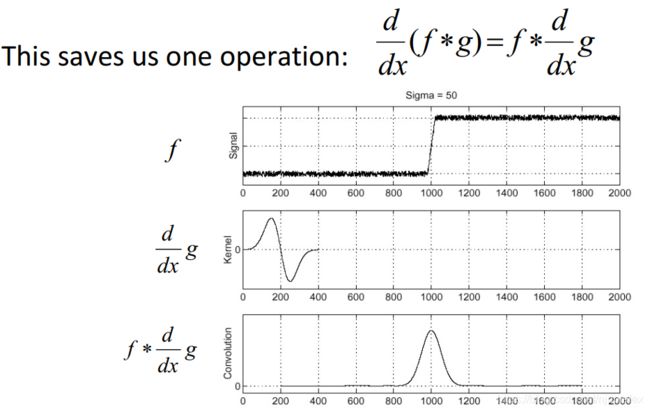
image 看作信号，边缘看作出现了脉冲信号，检测脉冲信号的位置，对信号波形求导，找极值点
搞视觉的方便起见，delta = 1，距离为1的像素之间做差，再除以delta，近似为求导结果
∂ f ( x , y ) ∂ x = lim ε → 0 f ( x + ε , y ) − f ( x , y ) ε \frac{\partial f(x, y)}{\partial x}=\lim _{\varepsilon \rightarrow 0} \frac{f(x+\varepsilon, y)-f(x, y)}{\varepsilon} ∂x∂f(x,y)=ε→0limεf(x+ε,y)−f(x,y)
应用到图像中：
∂ f ( x , y ) ∂ x ≈ f ( x + 1 , y ) − f ( x , y ) 1 \frac{\partial f(x, y)}{\partial x} \approx \frac{f(x+1, y)-f(x, y)}{1} ∂x∂f(x,y)≈1f(x+1,y)−f(x,y)
图像求导实现：
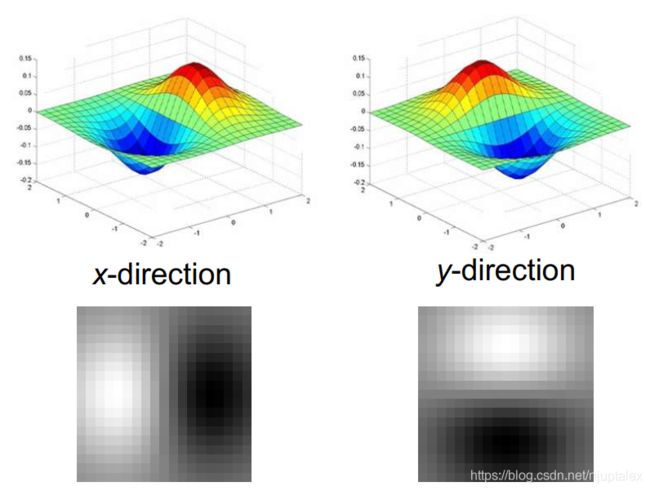
用【-1，1】的卷积核对原图操作，即对x方向求导，通常用【-1，0，1】用右边像素-左边像素来衡量我自己
可以求得某一像素的梯度的强度和方向，方向与边缘垂直，强度为勾股弦
其他的卷积核
Prewitt（利用左上左下右上右下像素来近似自己的梯度），
Sobel（卷积核可以分离为两个向量成绩，第一个高斯滤波向量，第二个边缘提取向量，对噪声鲁棒），
Roberts（用斜上方-自己，近似自己的梯度）
噪声对边缘提取有很大影响，一般需要先用一个卷积核去噪，再求梯度
运算速度更快：先对卷积核求梯度，再乘上原图
高斯核梯度可视化
回顾：
- 平滑核：高斯滤波去除高频；卷积核总和=1，保证不改变原图的强度
- 梯度核：有负值；卷积核总和=1，保证平坦区域不会检测出边缘
Canny算子：
- 高斯梯度滤波
- 计算梯度强度和方向
- 非最大化抑制，细化边缘
- 双门限，两头一夹
边缘检测 可以辅助图像分割
2. 拟合
边缘检测的线无法用数学描述；从问题出发，选择什么拟合算法
最小二乘
可以通过纯矩阵运算求得，缺点：无法拟合垂直的线
使用全最小二乘，到 ax+by=d 的距离最小，推导略
从极大似然估计的角度理解（妙啊）
假设每一个观测点是由噪声产生的，噪声又符合正态分布，距离所有观测点最近的直线 等价于 所有观测点对应的噪声的概率值都尽可能大（即epsilon–>0, Probability(epsilon)–>max）
所以，采取最大似然估计法。
P ( x 1 , y 1 , … , x n , y n ∣ a , b , d ) = ∏ i = 1 n P ( x i , y i ∣ a , b , d ) ∝ ∏ i = 1 n exp ( − ( a x i + b y i − d ) 2 2 σ 2 ) P\left(x_{1}, y_{1}, \ldots, x_{n}, y_{n} \mid a, b, d\right)=\prod_{i=1}^{n} P\left(x_{i}, y_{i} \mid a, b, d\right) \propto \prod_{i=1}^{n} \exp \left(-\frac{\left(a x_{i}+b y_{i}-d\right)^{2}}{2 \sigma^{2}}\right) P(x1,y1,…,xn,yn∣a,b,d)=i=1∏nP(xi,yi∣a,b,d)∝i=1∏nexp(−2σ2(axi+byi−d)2)
L ( x 1 , y 1 , … , x n , y n ∣ a , b , d ) = − 1 2 σ 2 ∑ i = 1 n ( a x i + b y i − d ) 2 L\left(x_{1}, y_{1}, \ldots, x_{n}, y_{n} \mid a, b, d\right)=-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{n}\left(a x_{i}+b y_{i}-d\right)^{2} L(x1,y1,…,xn,yn∣a,b,d)=−2σ21i=1∑n(axi+byi−d)2
Robust estimator
鲁棒的最小二乘，超过某一范围的点就不考虑了
原本的最小二乘，添加一个非线性变换
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NxTjs0Zg-1602489327194)(北京邮电大学计算机视觉（本科）.assets/image-20201010170002191.png)]
鲁棒估计是非线性优化问题，最小二乘求得的解可用作参数初始化；sigma一般选平均残差的1.5倍
RANSAC
应对比较多的偏离点，需要迭代求解，可用于指纹匹配
Hough
多条线拟合
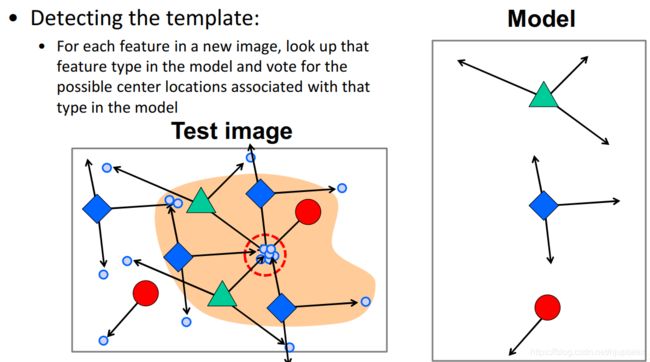
可用于汽车检测，训练车轮和车辆中心点的关系，确定每个局部组件的可能方向
测试新车时，首先检测车轮组件，得到方向，找到所有组件的集中的地方，为车的位置
Model selection
没有数学模型可以刻画，用模型估计，比如snake方法
3. Harris 角点
好的特征点：1）可重复可迁移 2）显著区分性大 3）紧凑 3）局部性
应用：图像对齐拼接，3D重建，动作追踪，物体识别，数据检索
角点：significant change in all directions
Harris 角点检测的过程
- 计算窗口内的能量函数
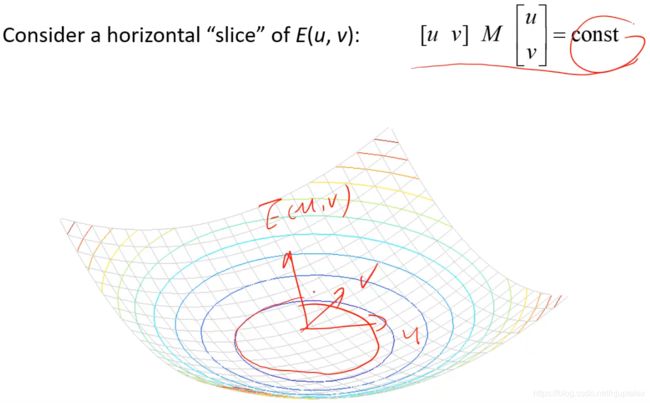
E ( u , v ) = ∑ x , y w ( x , y ) [ I ( x + u , y + v ) − I ( x , y ) ] 2 E(u, v)=\sum_{x, y} w(x, y)[I(x+u, y+v)-I(x, y)]^{2} E(u,v)=x,y∑w(x,y)[I(x+u,y+v)−I(x,y)]2
泰勒展开的原因：简化计算，使E变成与u,v直接关联的函数
E ( u , v ) ≈ E ( 0 , 0 ) + [ u v ] [ E u ( 0 , 0 ) E v ( 0 , 0 ) ] + 1 2 [ u v ] [ E u u ( 0 , 0 ) E u v ( 0 , 0 ) E u v ( 0 , 0 ) E v v ( 0 , 0 ) ] [ u v ] E(u, v) \approx E(0,0)+\left[\begin{array}{ll} u & v \end{array}\right]\left[\begin{array}{l} E_{u}(0,0) \\ E_{v}(0,0) \end{array}\right]+\frac{1}{2}\left[\begin{array}{lll} u & v \end{array}\right]\left[\begin{array}{cc} E_{u u}(0,0) & E_{u v}(0,0) \\ E_{u v}(0,0) & E_{v v}(0,0) \end{array}\right]\left[\begin{array}{l} u \\ v \end{array}\right] E(u,v)≈E(0,0)+[uv][Eu(0,0)Ev(0,0)]+21[uv][Euu(0,0)Euv(0,0)Euv(0,0)Evv(0,0)][uv]
E u ( u , v ) = ∑ x , y 2 w ( x , y ) [ I ( x + u , y + v ) − I ( x , y ) ] I x ( x + u , y + v ) E u u ( u , v ) = ∑ x , y 2 w ( x , y ) I x ( x + u , y + v ) I x ( x + u , y + v ) + ∑ x , y 2 w ( x , y ) [ I ( x + u , y + v ) − I ( x , y ) ] I x x ( x + u , y + v ) E u v ( u , v ) = ∑ x , y 2 w ( x , y ) I y ( x + u , y + v ) I x ( x + u , y + v ) + ∑ x , y 2 w ( x , y ) [ I ( x + u , y + v ) − I ( x , y ) ] I x y ( x + u , y + v ) \begin{aligned} E_{u}(u, v) &=\sum_{x, y} 2 w(x, y)[I(x+u, y+v)-I(x, y)] I_{x}(x+u, y+v) \\ E_{u u}(u, v) &=\sum_{x, y} 2 w(x, y) I_{x}(x+u, y+v) I_{x}(x+u, y+v)+\sum_{x, y} 2 w(x, y)[I(x+u, y+v)-I(x, y)] I_{x x}(x+u, y+v) \\ E_{u v}(u, v) &=\sum_{x, y} 2 w(x, y) I_{y}(x+u, y+v) I_{x}(x+u, y+v)+\sum_{x, y} 2 w(x, y)[I(x+u, y+v)-I(x, y)] I_{x y}(x+u, y+v) \end{aligned} Eu(u,v)Euu(u,v)Euv(u,v)=x,y∑2w(x,y)[I(x+u,y+v)−I(x,y)]Ix(x+u,y+v)=x,y∑2w(x,y)Ix(x+u,y+v)Ix(x+u,y+v)+x,y∑2w(x,y)[I(x+u,y+v)−I(x,y)]Ixx(x+u,y+v)=x,y∑2w(x,y)Iy(x+u,y+v)Ix(x+u,y+v)+x,y∑2w(x,y)[I(x+u,y+v)−I(x,y)]Ixy(x+u,y+v)
带入值
E ( 0 , 0 ) = 0 E u ( 0 , 0 ) = 0 E v ( 0 , 0 ) = 0 \begin{array}{l} E(0,0)=0 \\ E_{u}(0,0)=0 \\ E_{v}(0,0)=0 \end{array} E(0,0)=0Eu(0,0)=0Ev(0,0)=0
E u u ( 0 , 0 ) = ∑ x , y 2 w ( x , y ) I x ( x , y ) I x ( x , y ) E v v ( 0 , 0 ) = ∑ x , y 2 w ( x , y ) I y ( x , y ) I y ( x , y ) E u v ( 0 , 0 ) = ∑ x , y 2 w ( x , y ) I x ( x , y ) I y ( x , y ) \begin{aligned} E_{u u}(0,0) &=\sum_{x, y} 2 w(x, y) I_{x}(x, y) I_{x}(x, y) \\ E_{v v}(0,0) &=\sum_{x, y} 2 w(x, y) I_{y}(x, y) I_{y}(x, y) \\ E_{u v}(0,0) &=\sum_{x, y} 2 w(x, y) I_{x}(x, y) I_{y}(x, y) \end{aligned} Euu(0,0)Evv(0,0)Euv(0,0)=x,y∑2w(x,y)Ix(x,y)Ix(x,y)=x,y∑2w(x,y)Iy(x,y)Iy(x,y)=x,y∑2w(x,y)Ix(x,y)Iy(x,y)
则E简化为
E ( u , v ) ≈ [ u v ] M [ u v ] M = ∑ x , y w ( x , y ) [ I x 2 I x I y I x I y I y 2 ] E(u, v) \approx\left[\begin{array}{lll} u & v \end{array}\right] M\left[\begin{array}{l} u \\ v \end{array}\right] \\ M=\sum_{x, y} w(x, y)\left[\begin{array}{cc} I_{x}^{2} & I_{x} I_{y} \\ I_{x} I_{y} & I_{y}^{2} \end{array}\right] E(u,v)≈[uv]M[uv]M=x,y∑w(x,y)[Ix2IxIyIxIyIy2]
其中，E(u, v) 是一个二次方程，可表示成一个二次曲面，E(u,v)取常数值的时候，得到关于u，v的椭圆切面
通过分析M矩阵，就可以知道窗口的能量
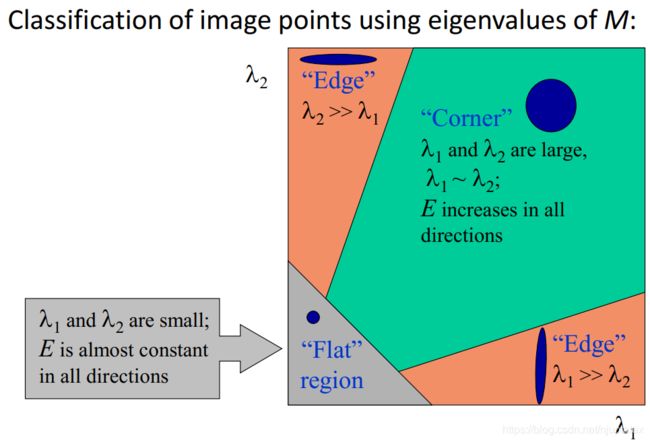
分析M矩阵（二阶矩矩阵）：
当x，y方向正交时，IxIy=0
M = ∑ x , y w ( x , y ) [ I x 2 I x I y I x I y I y 2 ] = [ λ 1 0 0 λ 2 ] M=\sum_{x, y} w(x, y)\left[\begin{array}{cc} I_{x}^{2} & I_{x} I_{y} \\ I_{x} I_{y} & I_{y}^{2} \end{array}\right]=\left[\begin{array}{cc} \lambda_{1} & 0 \\ 0 & \lambda_{2} \end{array}\right] M=x,y∑w(x,y)[Ix2IxIyIxIyIy2]=[λ100λ2]
若Iy=0，E=lamda1u^2，v再怎么变化，E都不变化，于是检测不出v方向；所以lamda1和lamda2都要较大
E的椭圆切片可视化：
M 矩阵可以分解出旋转矩阵
M = R − 1 [ λ 1 0 0 λ 2 ] R M=R^{-1}\left[\begin{array}{ll} \lambda_{1} & 0 \\ 0 & \lambda_{2} \end{array}\right] R M=R−1[λ100λ2]R
特征值的大小决定了椭圆的长短轴，R决定了椭圆的旋转角度
每一个像素点都可以绘制一个椭圆：
可以看出，沿着长轴信号变化缓慢（lamda小），沿着短轴信号变化激烈（lamda大）
与旋转矩阵R没啥关系：Harris具有旋转不变性
-
计算完窗口的能量函数之后，得到二阶矩矩阵，和其特征值后
计算 响应值 以判断lamda1 是不是和 lamda2 差不太多
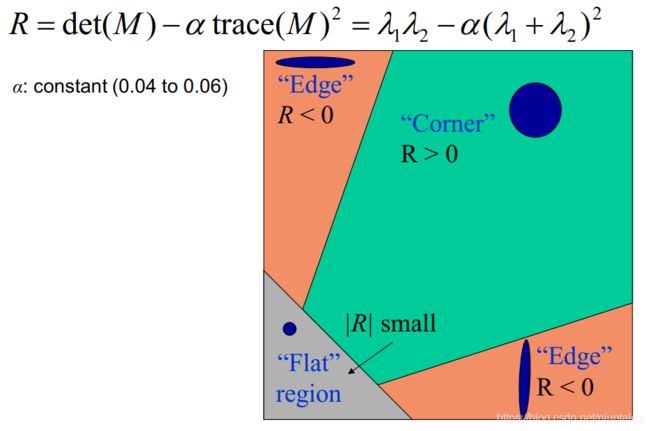
作者设计了一个响应函数：
R = det ( M ) − α trace ( M ) 2 = λ 1 λ 2 − α ( λ 1 + λ 2 ) 2 R=\operatorname{det}(M)-\alpha \operatorname{trace}(M)^{2}=\lambda_{1} \lambda_{2}-\alpha\left(\lambda_{1}+\lambda_{2}\right)^{2} R=det(M)−αtrace(M)2=λ1λ2−α(λ1+λ2)2 -
每一个像素计算响应值之后，过滤
-
最大化抑制
Harris 角点的特性
Invariance 不变性: 图像变换之后，检测到的角点不变
Covariance 协相关不变性：图像变换之后，再叠加变换，又能使得检测到的角点不变
平移，旋转不变性
不具有尺度不变性
Partially invariant to affine intensity change
Corner location is covariant w.r.t translation
Corner location is covariant w.r.t rotation
Corner location is not covariant to scaling
4.尺度不变区域与SIFT特征
LoG算子 Laplacian of Gaussian
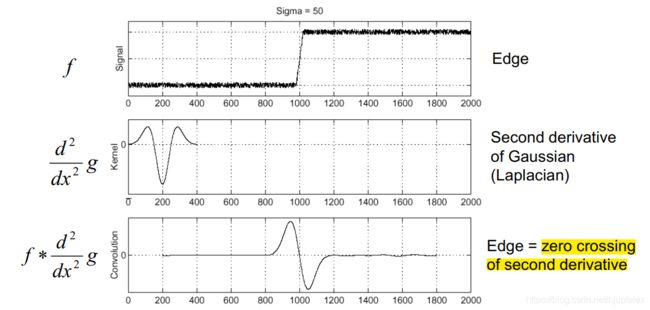
边缘提取的时候我们是用高斯(平滑作用)一阶导对原图做卷积，边缘出现在一阶导最大处
若用高斯二阶导做卷积，边缘出现再二阶导零点处
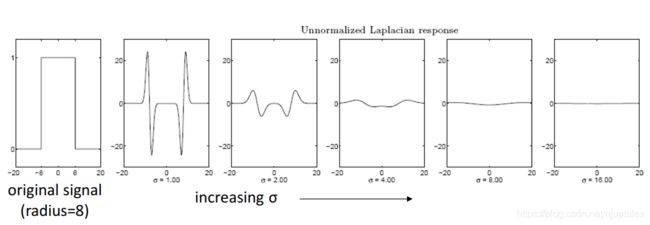
但是拉普拉斯响应（原始信号经过拉普拉斯卷积后得到拉普拉斯响应）会随sigma增加而衰弱
随着方差增加，高斯一阶导的相应衰弱，需要补偿一个sigma
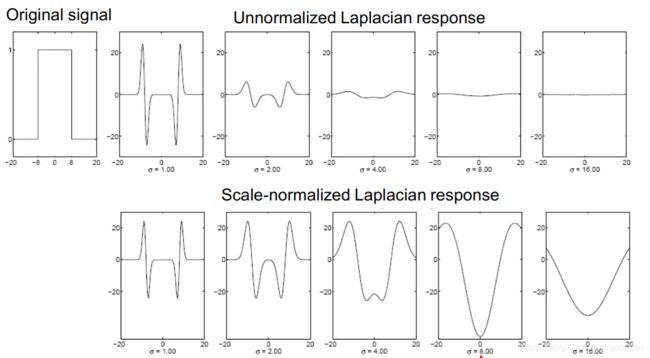
对应拉普拉斯响应，需要补偿sigma平方
Scale-normalized 后效果：
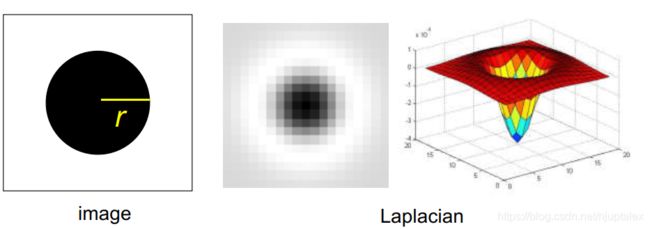
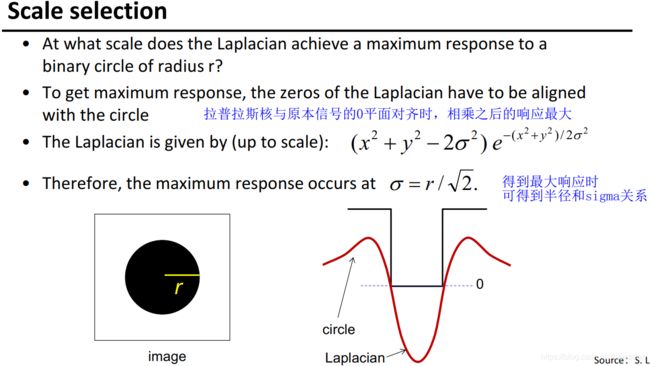
利用拉普拉斯核找blob区域：
拉普拉斯响应最大时，blob的半径和方差的关系为
σ = r / 2 \sigma=r / \sqrt{2} σ=r/2
检测到blob时，image中的黑圈圈和拉普拉斯的黑圈圈刚好对上
小sigma检测小圆圈，大sigma检测大圆圈，
用3个不同的尺度（不同的sigma）对原图卷积，取3个响应最大的那个，以该像素为中心，画一个半径为根号二倍sigma的圈。也是需要非最大化抑制的；
Scale-space blob detector
尺度越大，检测越慢
应用：
Harris-Laplacian：Harris解决光照，平移，旋转，拉普拉斯解决尺度不变性
SIFT特征：Scale-Invariant Keypoints IJCV 2004
SIFT 特征
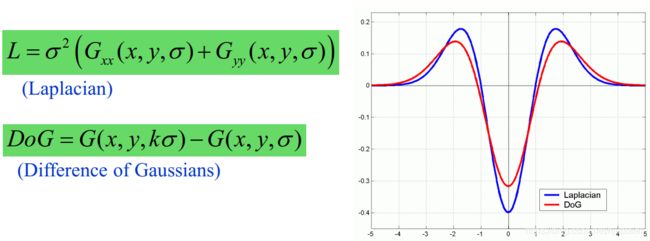
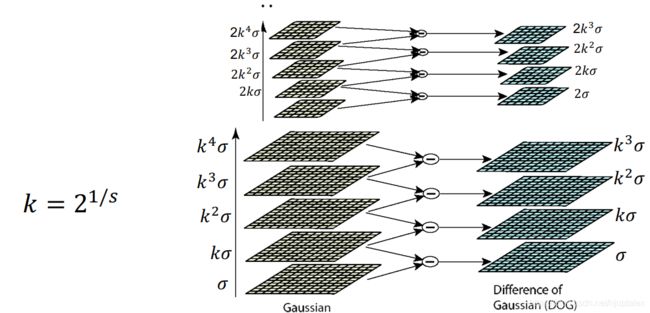
DoG算子
DoG算子（高斯核之差）和Laplacian算子（高斯二阶导，补偿sigma平方）大致差一个常数倍；Laplacian算子太慢
1）尺度空间极值检测：通过使用高斯差分函数来计算并搜索所有尺度上的图像位置，用于识别对尺度和方向不变的潜在兴趣点。
2）关键点定位：通过一个拟合精细的模型在每个候选位置上确定位置和尺度
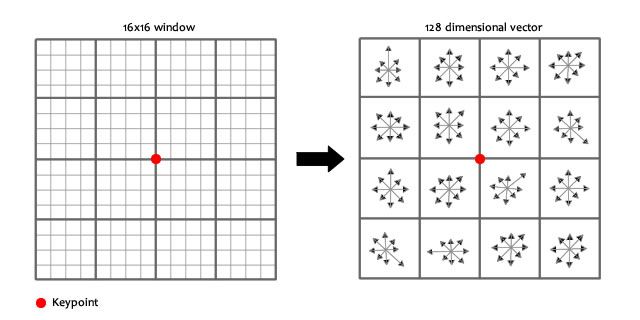
它以检测得到的关键点为中心，选择一个16 * 16的邻域，然后再把这个邻域再划分为4 * 4的子区域，然后对梯度方向进行划分成8个区间，这样在每个子区域内就会得到一个4 * 4 * 8=128维的特征向量，向量元素大小为每个梯度方向区间权值。提出得到特征向量后要对邻域的特征向量进行归一化，归一化的方向是计算邻域关键点的主方向，并将邻域旋转至根据主方向旋转至特定方向，这样就使得特征具有旋转不变性。然后再根据邻域内各像素的大小把邻域缩放到指定尺度，进一步使得特征描述子具有尺度不变性。
