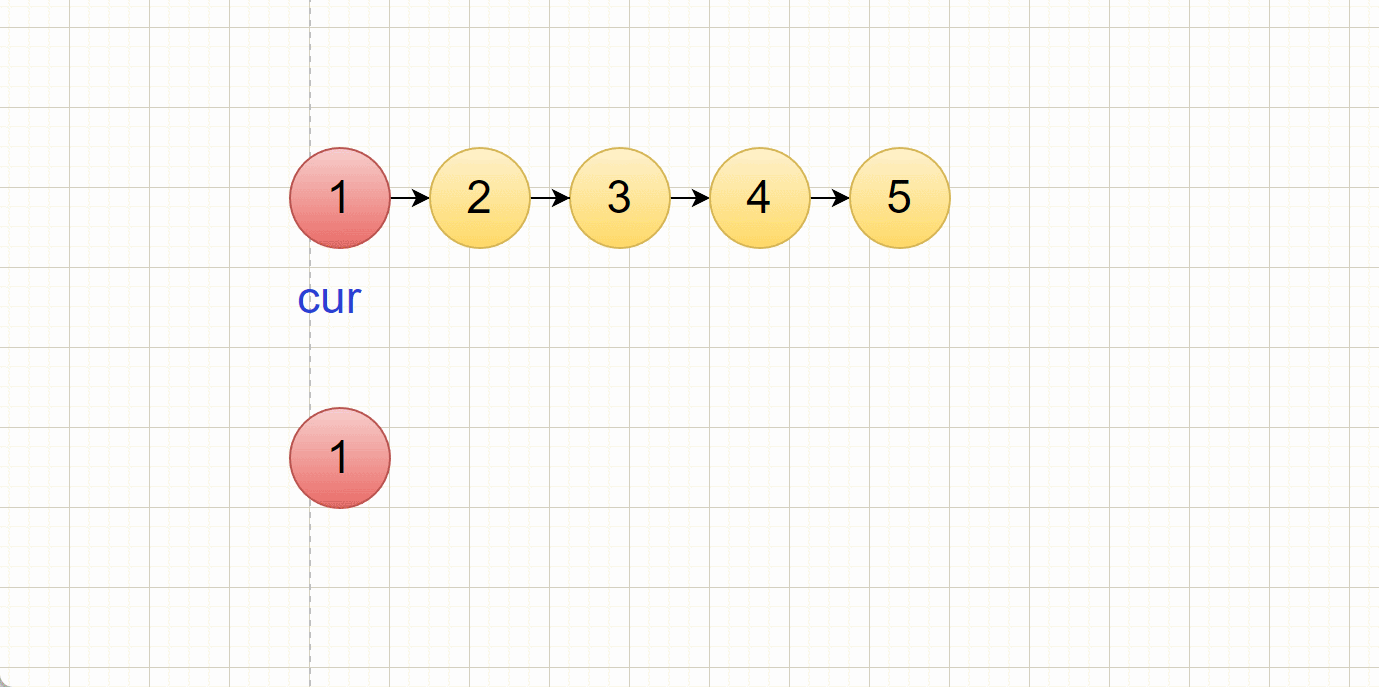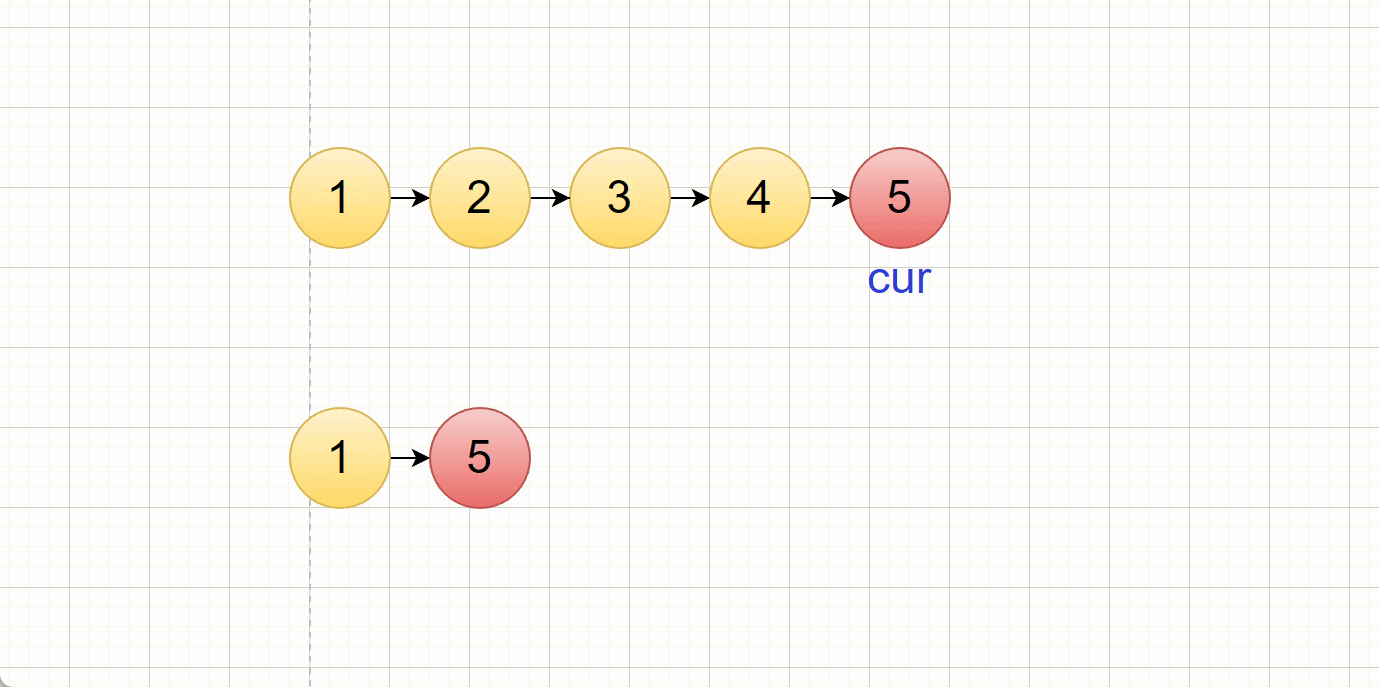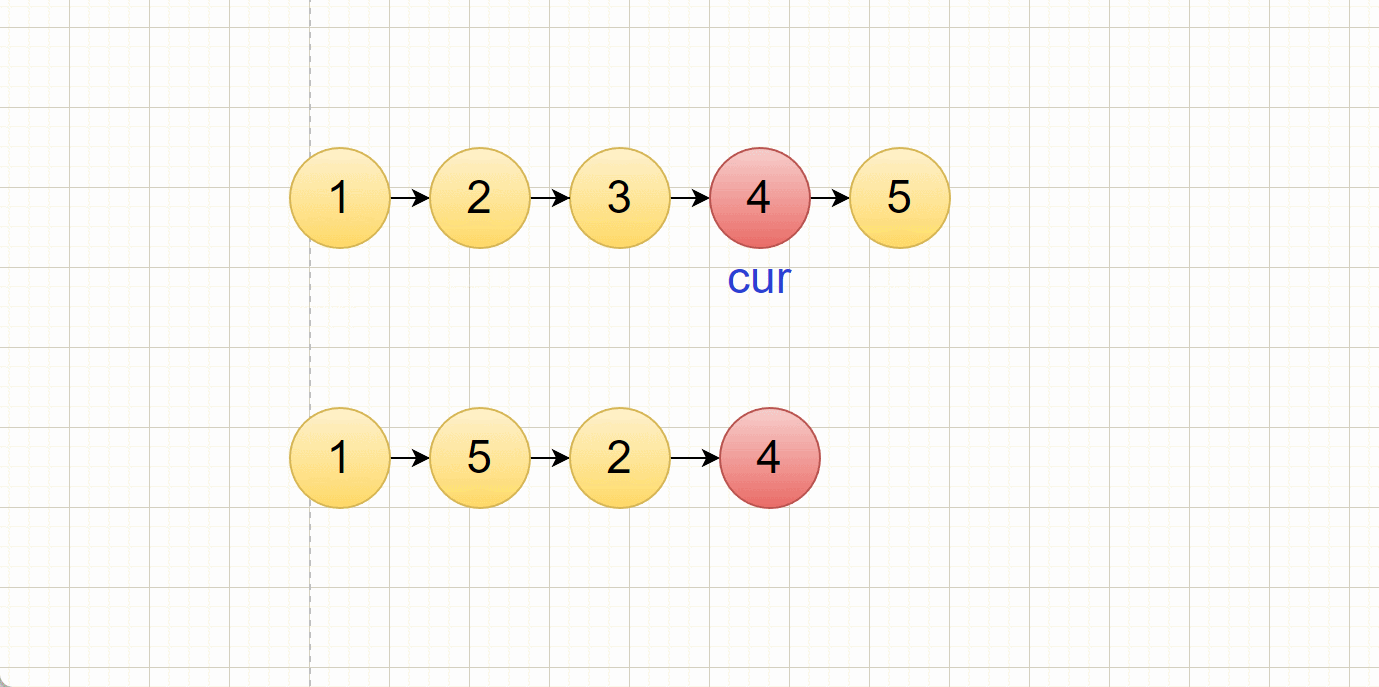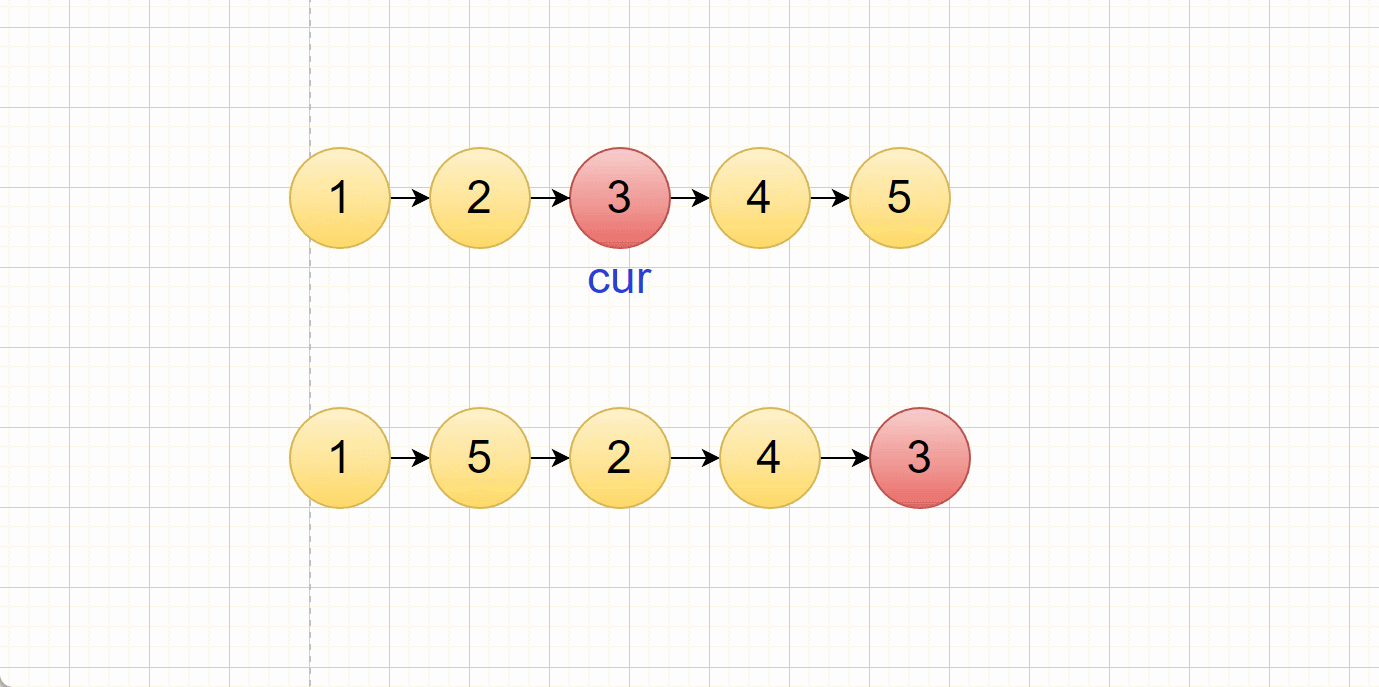五道LeetCode《中等难度》的单链表题
五道单链表中等难度题型
- 1. 剑指 Offer II 021. 删除链表的倒数第 n 个结点
-
- 第一种解法(单指针):
- 第二种解法(栈):
- 第三种解法(双指针):
- 2. 删除排序链表中的重复元素 II(重点)
-
- 普通状态
- 特殊状态(头结点重复时)
- 特殊状态(删除尾结点时)
- 3. 删除链表中的节点
- 4. 重排链表
-
- 思路一:
- 思路二(寻找链表中点 + 链表逆序 + 合并链表)
- 5. 剑指 Offer II 077. 链表排序(重点!)
1. 剑指 Offer II 021. 删除链表的倒数第 n 个结点
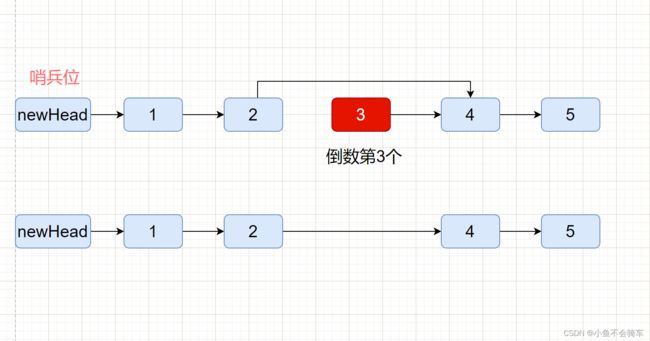
找到链表的倒数第n个结点,并删除该结点
三种解法:
第一种解法(单指针):
1.遍历链表,求出链表长度 L
2.链表长度 L 减去 n ,就是倒数第 n 个结点
3.找到倒数第 n 个结点的前驱结点,让前驱结点的 next 指向倒数第 n 个结点的后一个结点。
4.倒数的n个结点的前驱结点,就是 L-n+1
5.因为如果要删除的是头节点,要删除的头节点没有先驱结点,所以设置一个哨兵位
6.哨兵位的 next 指向 head ,这样头结点删除的情况也被转化为了通用情况
代码如下:
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0, head);//设置哨兵位
int length = getLength(head);//求出链表长度
ListNode cur = dummy;//用cur去遍历
//遍历L-n+1次就是要删除结点的前驱结点
for (int i = 1; i < length - n + 1; ++i) {
cur = cur.next;
}
//前驱结点的next指向要删除结点的后一个结点
cur.next = cur.next.next;
return dummy.next;
}
//求出链表长度
public int getLength(ListNode head) {
int length = 0;
while (head != null) {
++length;
head = head.next;
}
return length;
}
}
作者总结:
如果要删除的结点是最后一个结点,那么该代码的时间复杂度会达到 2×n ,虽然不是很慢,但是依旧没有达到想要的效果。
复杂度分析:
- 时间复杂度O(n),其中
N是给定链表中的结点数目。- 空间复杂度O(1)
第二种解法(栈):
实现思路:
我们可以在遍历链表的同时,顺便将链表中的结点依次存放到栈上,根据栈「先进后出」的原则,我们栈中弹出的第n个结点,就是我们要删除的结点,并且目前栈顶的节点就是待删除节点的前驱节点。这样一来,删除操作就变得十分方便了。
具体实现:
1.创建一个栈,将链表中的结点依次压入栈中
2.当链表遍历完成之后,依次从栈中弹出结点,到第n个结点时,就是我们要删除的结点
3.由于当前栈顶的结点刚好时第n个结点前驱结点,所以将栈顶的结点的next指向第 n 个结点的 next 就可以
4.由于需要考虑要删除的是头节点,所以我们设置一个哨兵位,这样即使要删除的结点是头节点,处理方法也和普通结点一样。
如图:
代码如下:
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0, head);//创建哨兵位
Deque<ListNode> stack = new LinkedList<ListNode>();//创建一个栈
ListNode cur = dummy;//cur代替哨兵位遍历
while (cur != null) {
//依次放入
stack.push(cur);
cur = cur.next;
}
//弹出倒数n个结点
for (int i = 0; i < n; ++i) {
stack.pop();
}
//当前栈顶就是要删除结点的前驱结点
ListNode prev = stack.peek();
//
prev.next = prev.next.next;
return dummy.next;
}
}
作者总结:
栈最大的特点是先进后出,所以逆序输出是栈经常用到的一个应用场景。首先把所有元素依次入栈,然后把所有元素出栈并输出,这样就实 现了逆序输出。
复杂度分析:
- 时间复杂度O(n),其中
N是给定链表中的结点数目。- 空间复杂度O(n),其中
N是链表的长度,主要为栈的开销。
第三种解法(双指针):
解题思路:
通过双指针,由于是删除倒数第 n 个结点,所以我们可以用距离的差,快指针先走 n+1 步,接下来两个指针一起走,当快指针为空时,此时的慢指针就是倒数第n-1个结点( n-1 是 n 的前驱结点)。
具体实现:
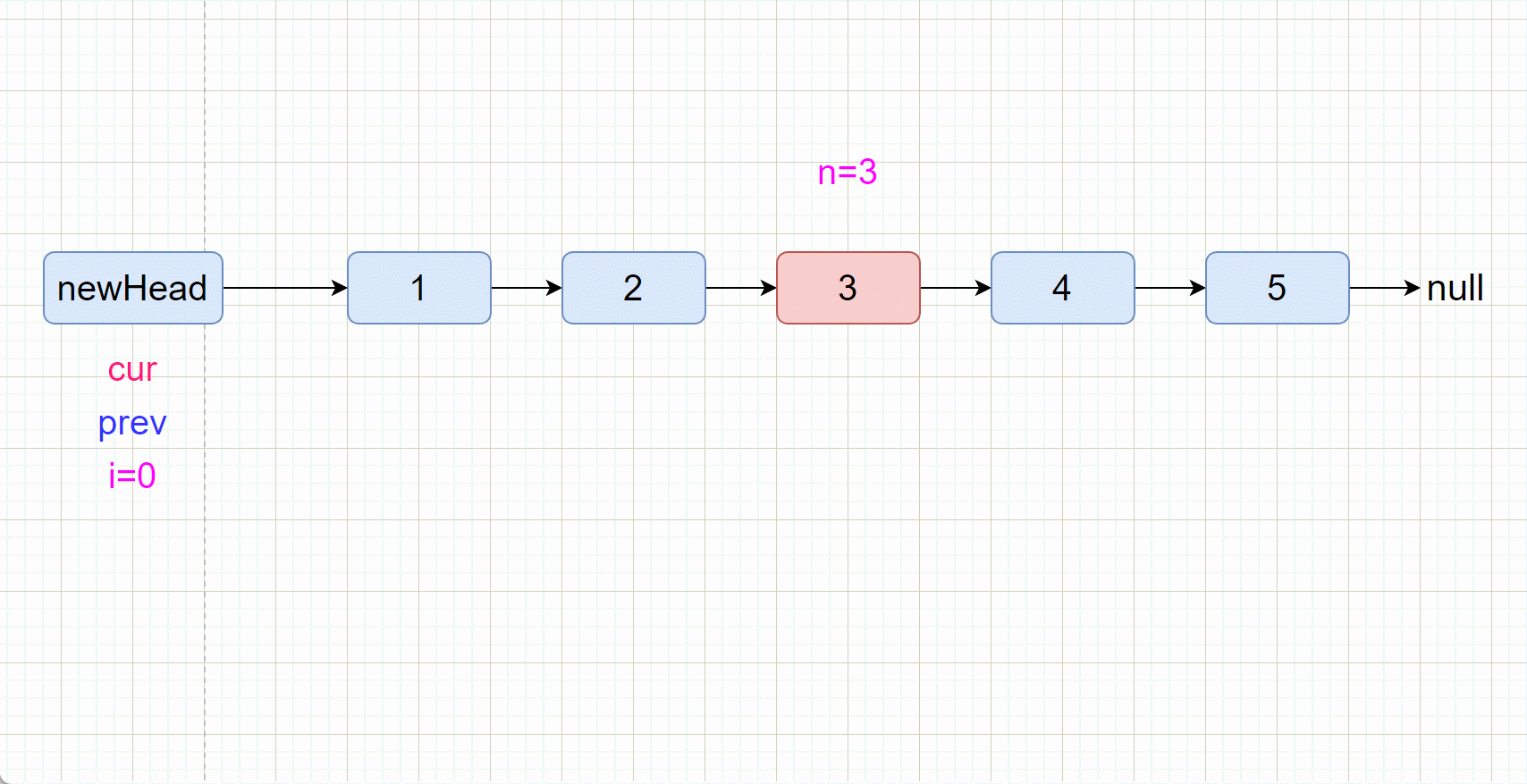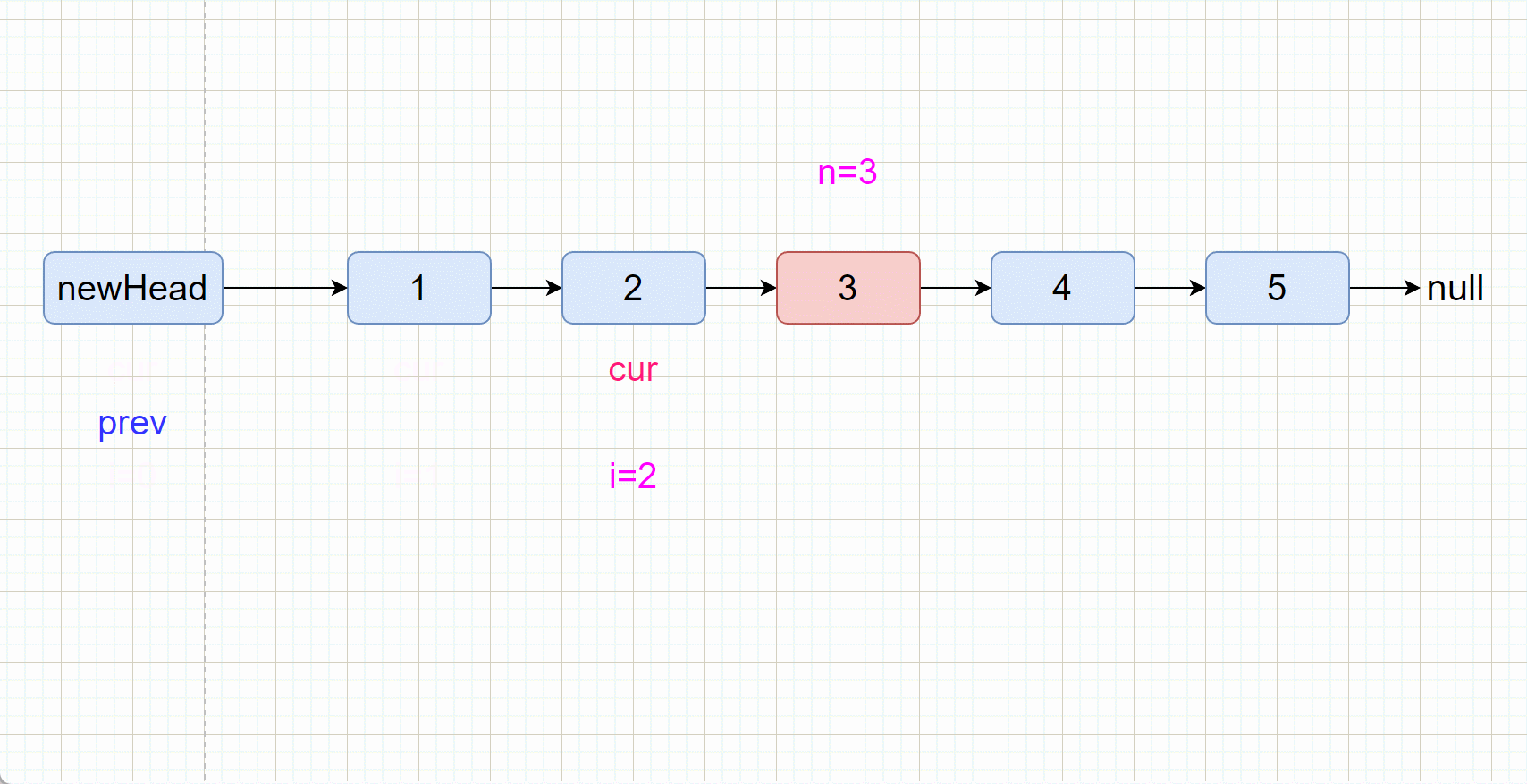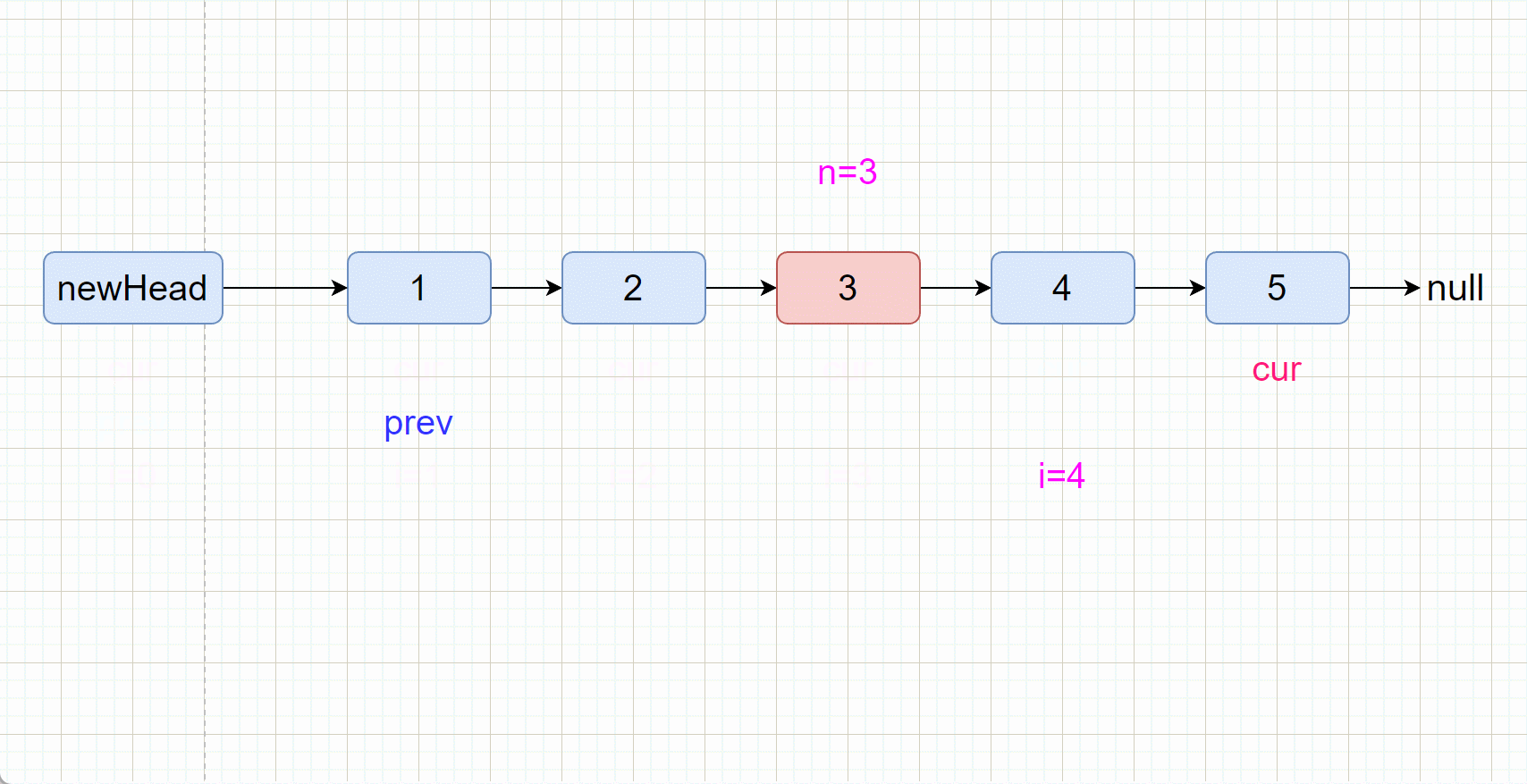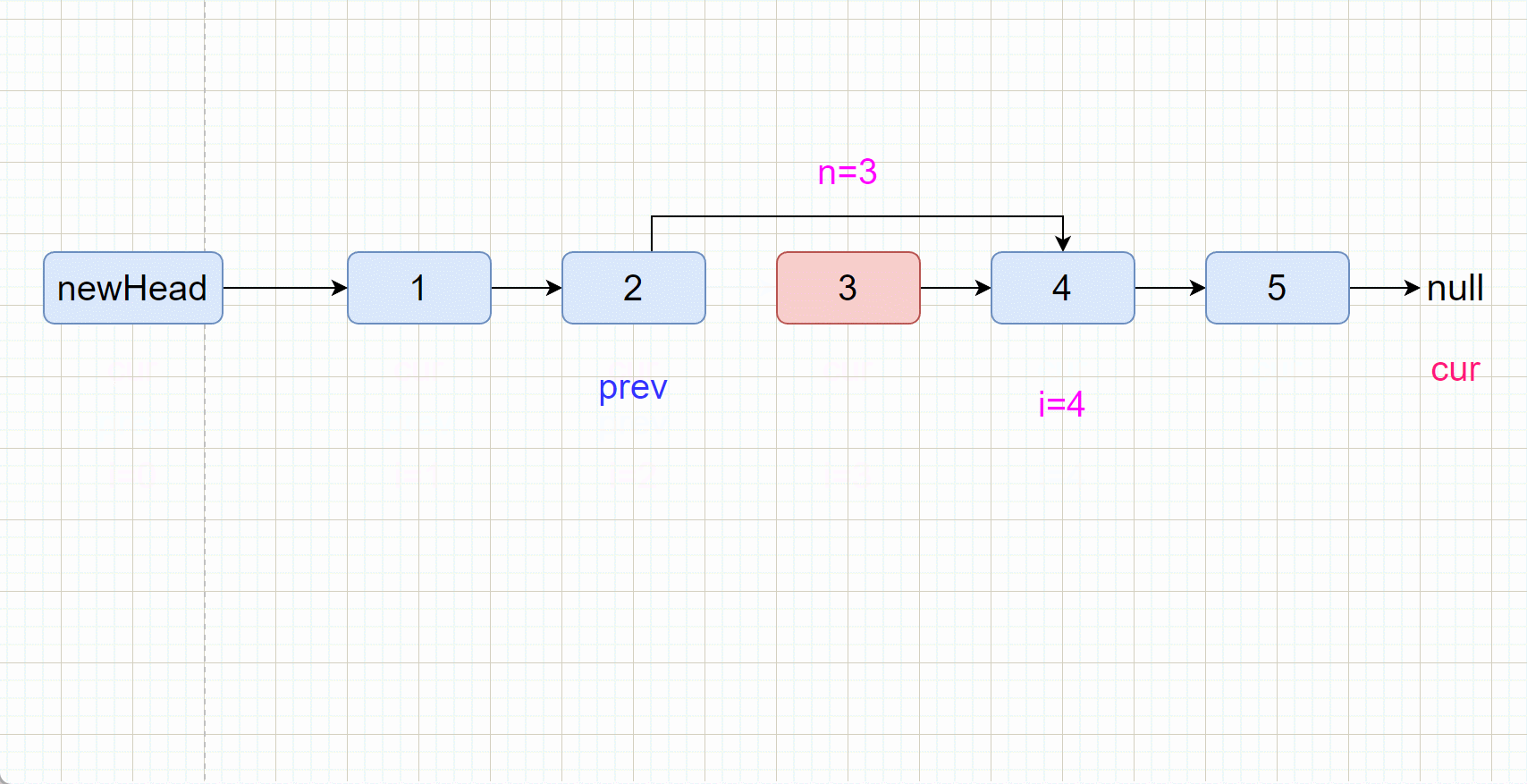
- 定义两个指针,cur 和 prev
- cur先走 n+1 步,然后两个指针一起向后遍历,直到cur为空时,此时prev就是要删除结点的前驱结点,
prev.next=prev.next.next就行。- 定义一个哨兵位,使 cur 和 prev 最开始都指向
newHead
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
//判断是否为空
if(head==null) {
return head;
}
//创建一个哨兵位
ListNode newHead=new ListNode(0);
//哨兵位的next指向head
newHead.next=head;
//将cur和prev同时指向newHead
ListNode cur=newHead;
ListNode prev=newHead;
//快指针先走n+1步(也可以快指针总head走,走n步就可以,核心思路就是慢指针要和快指针之间的距离差1)
for(int i=0;i<n+1;i++) {
cur=cur.next;
}
//两个指针一起走
while(cur!=null) {
cur=cur.next;
prev=prev.next;
}
//最后删除倒数第n个结点
prev.next=prev.next.next;
//返回newHead的next
return newHead.next;
}
}
作者总结:
不同于之前做的找到倒数第k个结点,该题是要删除倒数第k个结点,所以我们需要找到倒数第k个数的前驱节点,核心思路就是,快指针和慢指针最开始的距离差要为 n+1,不论是相同位置快指针先走 n+1 步,又或者慢指针是快指针的前一个结点,快指针走 n 步,最终要到达的目的都是和快指针的距离为 n+1,所以掌握核心思路,再去思考这道题就会很轻松。
复杂度分析:
- 时间复杂度O(n),其中
N是给定链表中的结点数目。- 空间复杂度O(1)。
2. 删除排序链表中的重复元素 II(重点)
题目描述:
将有序链表中所有重复出现的数,都删除掉,只留下出现一次的数字。
需要考虑的事项:
- 考虑头删和尾删,
- 注意空指针异常,
一种普通状态:
1->2->3->3->4->4->5->null (中间删)
两种特殊状态:
1->1->1->2->3->null (头删)
1->2->3->3->3->null (尾删)
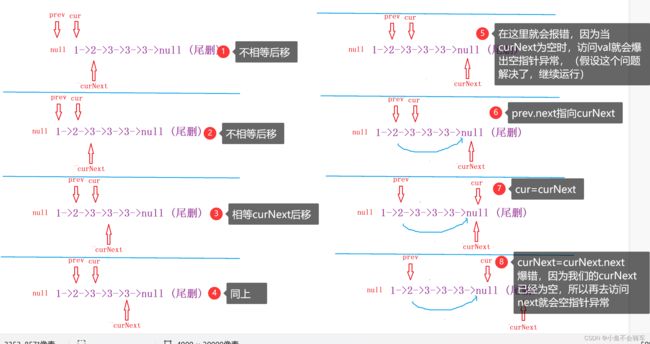
普通状态
解题思路:
- 定义三个指针,
prev cur curNext- 判断 cur 和 curNext 他们的 val 是否相等,如果不相等则把 cur 给 prev, curNext 给 cur,curNext=curNext.next.
如图:
重复上述操作,直到
cur.val == curNext.val
再次判断
curNext.val == cur.val是否为真,如果为真,继续重复上述操作,
最后运行结果:
特殊状态(头结点重复时)
如果此时依旧是通过上述的代码运行,会爆出空指针异常的错误,因为的的 prev 是 null ,所以prev.next 就会产生空指针异常,解决的方法就是,判断是否是头删,如果是头删则
head=curNext,将头节点后移。
此时我们的头删就完成了
运行结果:
特殊状态(删除尾结点时)
这里需要注意空指针异常,具体细节如下
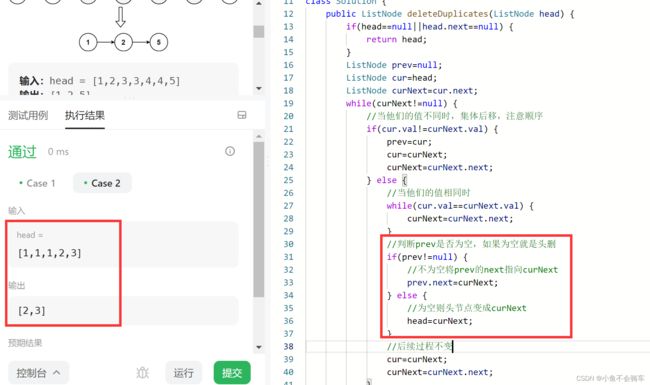
class Solution {
public ListNode deleteDuplicates(ListNode head) {
if(head==null||head.next==null) {
return head;
}
ListNode prev=null;
ListNode cur=head;
ListNode curNext=cur.next;
while(curNext!=null) {
//当他们的值不同时,集体后移,注意顺序
if(cur.val!=curNext.val) {
prev=cur;
cur=curNext;
curNext=curNext.next;
} else {
//当他们的值相同时,并且curNext不为空,进入循环
//注意要将curNext!=null的判断条件写在左边
//逻辑运算&&,先判断左边,如果左边为真才判断右边,
//当你的curNext!=null写在右边时,
//他会先进行curNext.val的操作,此时你的curNext已经为空
//再去访问就会发出空指针异常
while(curNext!=null&&cur.val==curNext.val) {
curNext=curNext.next;
}
//判断prev是否为空,如果为空就是头删
if(prev!=null) {
//不为空将prev的next指向curNext
prev.next=curNext;
} else {
//为空则头节点变成curNext
head=curNext;
}
//后续过程不变
cur=curNext;
//判断curNext是否为空,如果为空则不进行该操作
if(curNext!=null)
curNext=curNext.next;
}
}
return head;
}
}
作者总结:
这道题主要考虑的是答题人的细心程度,有一点不注意就有可能会造成越界访问,所以需要时刻注意可能会爆出错误的地方,并且我们自己画图会对写这种编程题有很大的益处,它可以帮我们找到平时没有注意到的小问题。
复杂度分析:
- 时间复杂度O(n),其中
N是给定链表中的结点数目。- 空间复杂度O(1)。
3. 删除链表中的节点
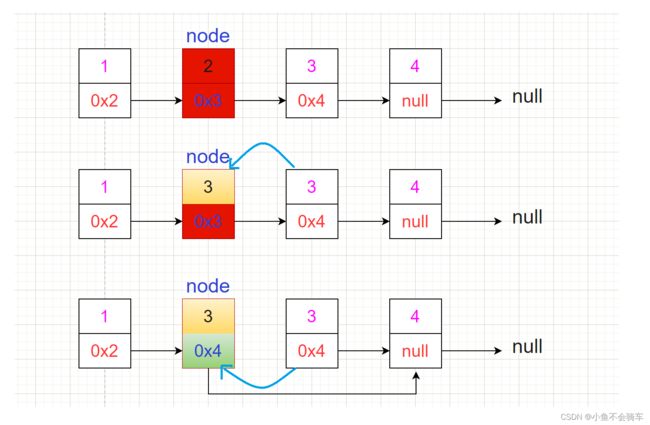
给你一个链表的结点,不能访问到头节点,要将链表的这个结点删除,
用例如下:1->2->3->4->5->null node=3;
输出为:1->2->4->5->null
解题思路:
题目中提到了,我们无法访问到头节点,在平时我们删除结点,都是找到要删除结点的前驱结点,让前驱结点的next指向要删除结点的下一个结点。
但是题目直接给了要删除的结点,我们无法访问的它的前一个结点,我们可以考虑,将下一个结点的 val 和 next 都给要删除的结点,由于下一个结点的next给了我们的node所以我们找不到原来的node的下一个结点,自然就完成了删除,如果是C语言需要释放内存,则可以提前保存下一个结点,最后free().
代码如下:
class Solution {
public void deleteNode(ListNode node) {
node.val=node.next.val;//替换为下一个结点的val
node.next=node.next.next;//替换为下一个结点的next
}
}
总结:
既然不能先删除自己,那就把自己整容成儿子,再假装自己就是儿子来养活孙子
复杂度分析:
- 时间复杂度O(1)
- 空间复杂度O(1)
4. 重排链表
题目描述:
解题思路:
思路一:
单链表并不支持随机访问,也不支持从后往前遍历,所以我们可以创建一个顺序表,将单链表中的结点一个一个存入顺序表中,最后根据下标来找到结点并重建链表。
具体实现:
- 构建一个顺序表
- 将链表存入到顺序表中
- 建立一个哨兵位,将后续重新排序的结点一个一个衔接在后面
代码如下:
class Solution {
public void reorderList(ListNode head) {
if(head==null||head.next==null) {
return;
}
//利用顺序表存储,然后按指定位置
//我这里没有直接使用库的顺序表,
ListNode [] array=new ListNode[50000];
ListNode cur=head;//
int i=0;
//从0下标存入
while(cur!=null) {
array[i]=cur;
cur=cur.next;
i++;
}
//最后i是元素个数
ListNode newHead=new ListNode(0);
ListNode newPrev=newHead;
int a=0;//a是下标
int b=i-1;//b也是下标,i是元素个数,元素个数-1就是最后一个元素的下标
int count=1;//根据奇偶判断读取哪个下标的元素
//最后i+1就是链表的结点个数+1,
//count是从1开始的,所以当count=i+1时,就代表读取完了所有结点
while(count!=i+1) {
//如果是奇数,就顺序读取
if(count%2!=0) {
newPrev.next=array[a];
newPrev=newPrev.next;
a++;//
} else{
//如果是偶数就逆序读取
newPrev.next=array[b];
newPrev=newPrev.next;
b--;
}
count++;
}
//将左后一个结点呢next置为kong,防止循环
newPrev.next=null;
//将头节点改为newHead的next
head=newHead.next;
}
}
复杂度分析:
- 时间复杂度O(n),n是链表的长度
- 空间复杂度O(n),n是顺序表的长度
思路二(寻找链表中点 + 链表逆序 + 合并链表)
思路二:
通过找到链表的中点,从中点将链表逆序,此时的实现和判断回文链表很是相似!将链表逆序后,一个结点从头开始,一个结点从逆序的链表的头开始,依次向后遍历,最后利用哨兵位合并这个链表
如图:
我们需要考虑的是合并链表的退出条件,如果是奇数个结点的链表,我们采取
cur!=prev,就会导致最后一个中间结点没有被合并到新链表中,所以需要单独考虑
具体步骤:
- 找到中间结点
- 逆序包含中间及后面的所以结点
- 合并单链表
代码如下(注意注释)
class Solution {
public void reorderList(ListNode head) {
if(head==null||head.next==null) {
return;
}
//找到中间结点
ListNode prev=head;//慢指针
ListNode cur=head;//快指针
while(cur!=null&&cur.next!=null) {
cur=cur.next.next;
prev=prev.next;
}
//逆序单链表
cur=reverse(prev);
prev=head;//prev从头遍历
ListNode newHead=new ListNode(0);
ListNode newPrev=newHead;
int i=1;//来判断调用谁的结点
while(true) {
if(i%2!=0) {
newPrev.next=prev;//衔接该结点
//当两个结点相等时退出循环
if(prev==cur) {
//并将newPrev置为下一个结点
newPrev=newPrev.next;
break;
}
prev=prev.next;//prev指向下一个结点
} else {
newPrev.next=cur;//衔接该结点
//当两个结点相等时退出循环
if(prev==cur) {
//并将newPrev置为下一个结点
newPrev=newPrev.next;
break;
}
cur=cur.next;//cur指向下一个结点
}
i++;
newPrev=newPrev.next;//置为下一个结点
}
newPrev.next=null;//将尾结点的next置为null,防止循环
}
//逆置链表函数
public ListNode reverse(ListNode head) {
ListNode prev=null;
ListNode cur=head;
while(cur!=null) {
ListNode curNext=cur.next;
cur.next=prev;
prev=cur;
cur=curNext;
}
return prev;
}
作者总结:
这道题作者最开始做的时候也没有思路,但是通过画图,也就慢慢的有了思路,关于我合并链表中,退出循环的条件,大家可以画图看一下,对应着图才能更好的掌握规律,包括作者为什么要将
if ( prev == cur )写在prev=prev.next或cur=cur.next的前面,大家可以画图思考一下,总之就是多画图,多思考,多上手敲代码。
复杂度分析:
- 时间复杂度O(n),n是链表的长度
- 空间复杂度O(1)
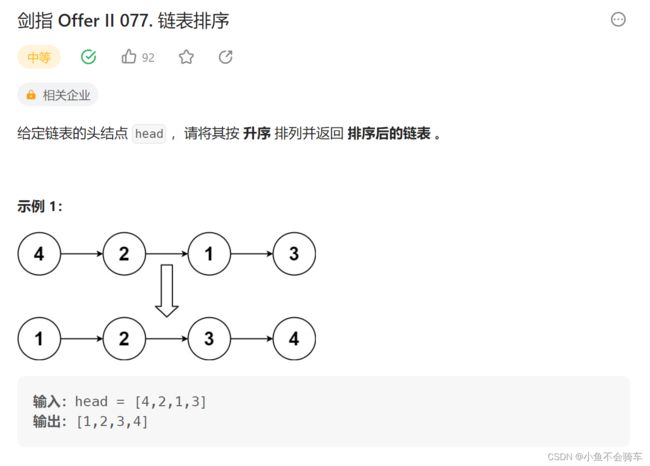
5. 剑指 Offer II 077. 链表排序(重点!)
题目描述:
给你一个无序链表,你需要将该链表排序
解题思路:
以链表的第一个结点为有序结点,后续结点和该有序链表的头进行对比,如果比头节点小,那就进行头插,如果比有序链表的尾小,那就尾插,否则就是中间插入。
如图:
我们先把会用到的指针都列举出来
ListNode cur=head.next;//后续链表的头指针
ListNode newhead=head;//当前有序链表的头指针
newhead.next=null;//与后续链表断开联系
ListNode prev=newhead;//有序链表向后遍历指针的前驱指针
ListNode prevNext=newhead.next;//用于有序链表向后遍历的指
针
ListNode last=newhead;//尾结点
ListNode curNext=cur.next;//用于找回后续链表的指针
具体实现:
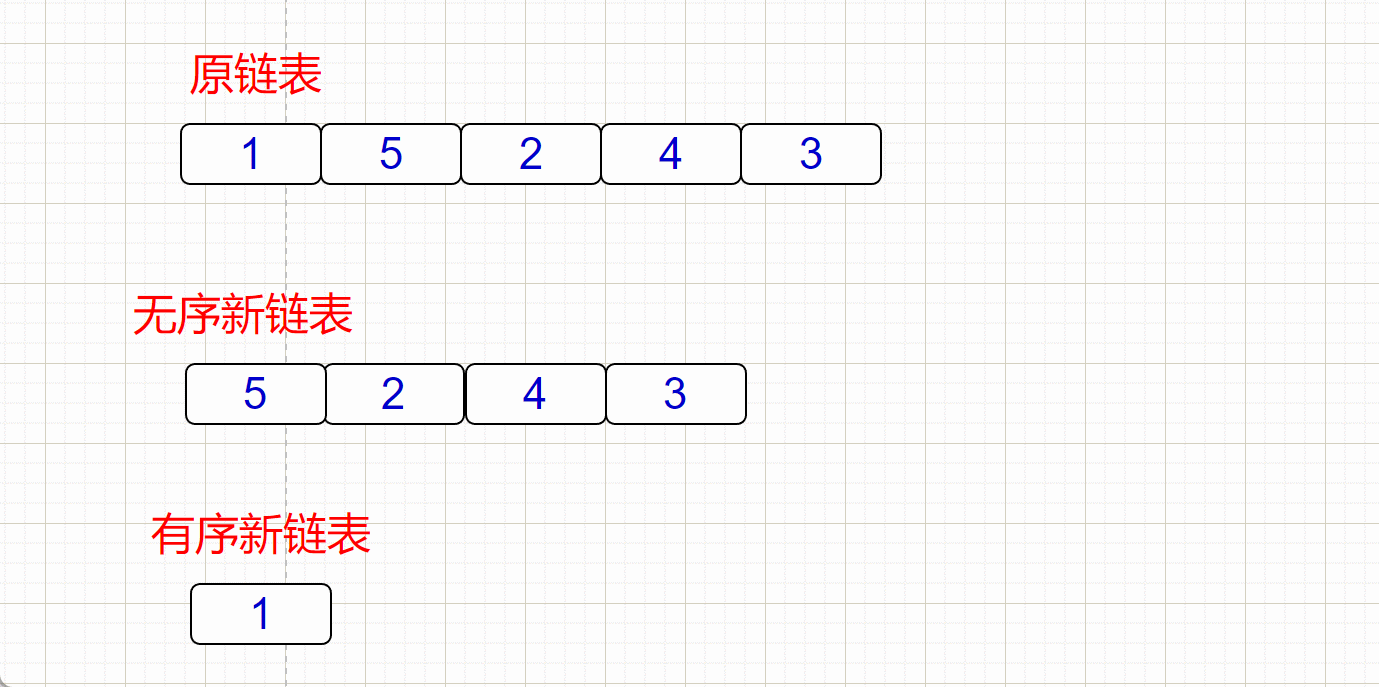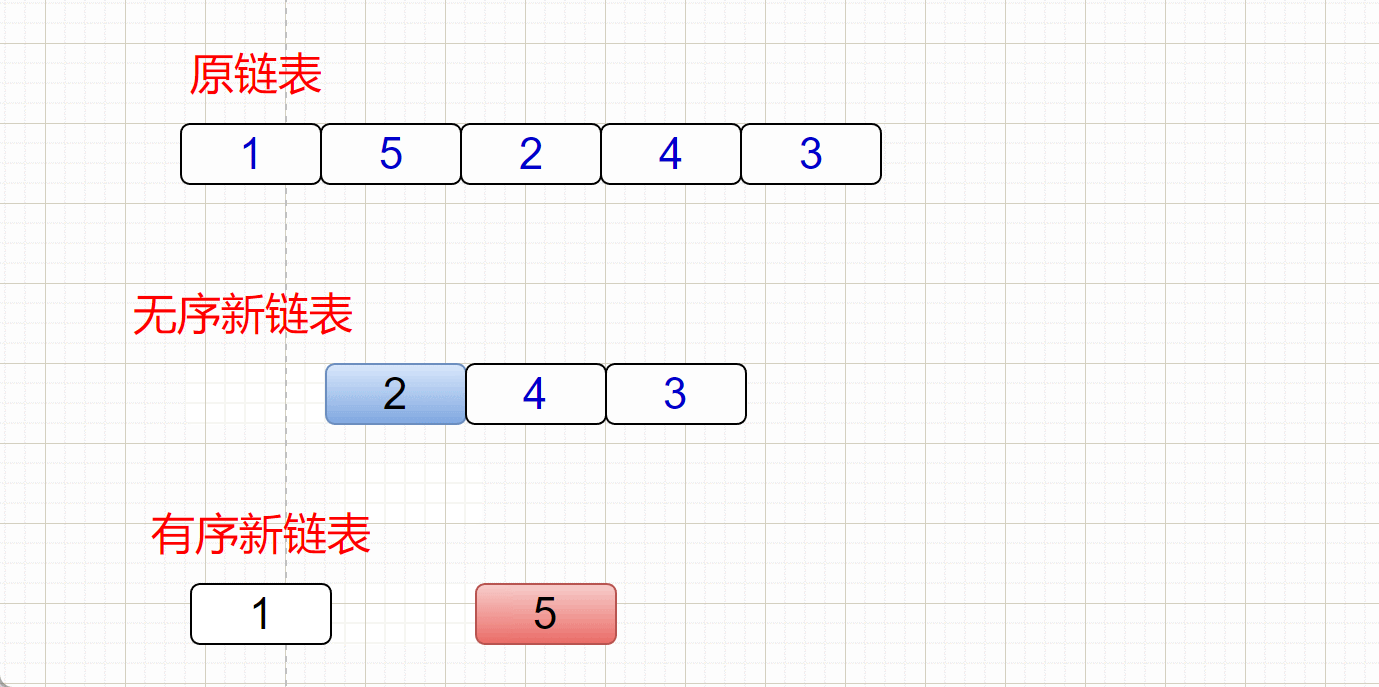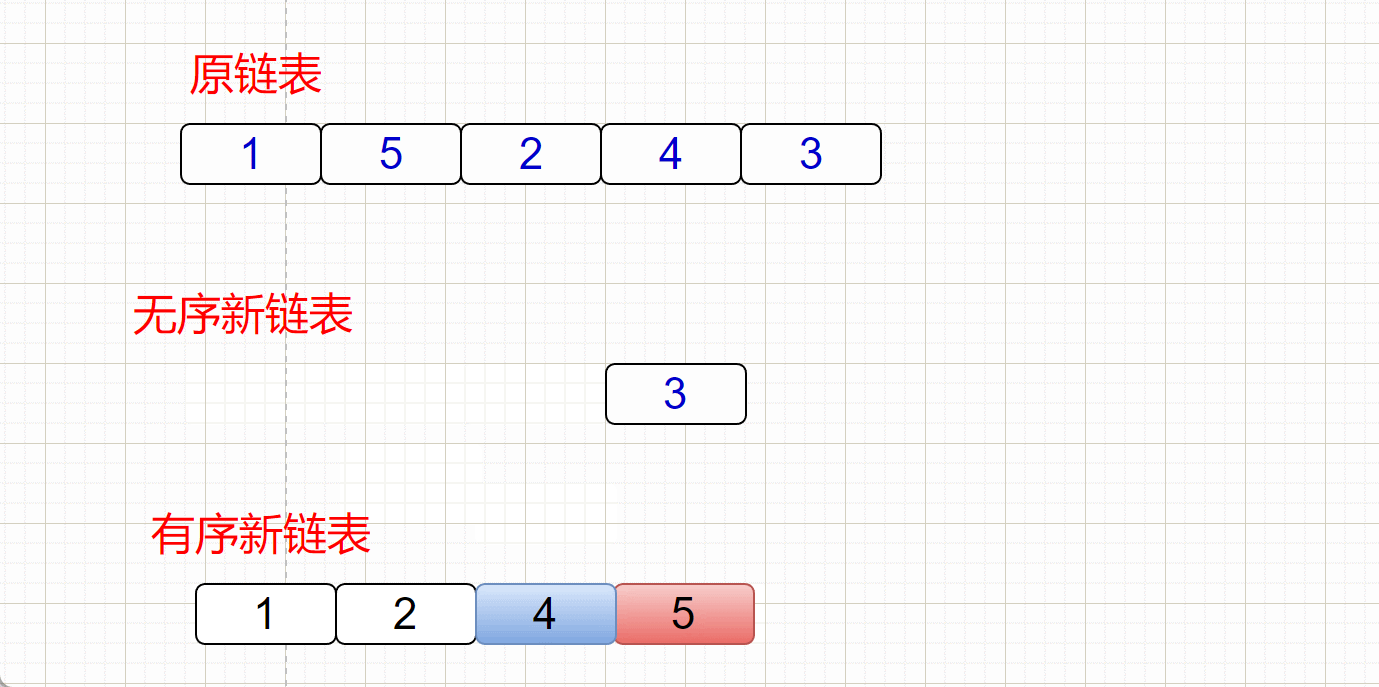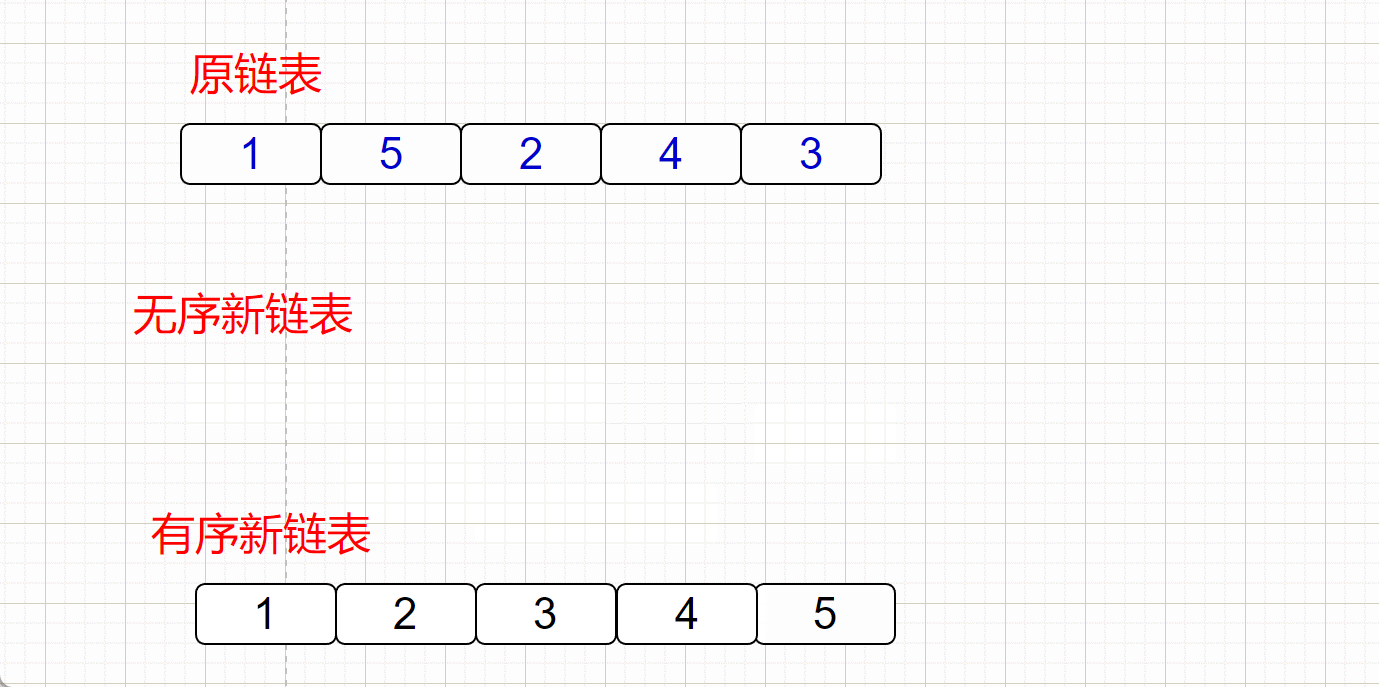
- 先将链表分割为一个有序链表,和一个无序链表
- 有序链表的头结点和无序链表中cur指向的结点进行对比,如果头节点小于cur对应的结点,就进行头插,
- 有序链表的尾结点和无序链表中的cur指向的结点进行对比,如果 尾结点小于cur对应的结点,那就代表这个链表没有比这个结点还要大的结点了,所以直接尾插就好了!
- 其余情况就是中间插入了,我们通过找到第一个比cur对应的结点的大的结点,将cur插入在该结点前面,完成中间插入
- 完成了插入后,让 prev 重新回归头节点的位置,即
prev=newHead,让 prevNext 重新成为有序链表的第二个结点,即prevNext=prev.next;
插入过程:
(有小瑕疵,cur跟尾结点比较的过程忽略了,直接按顺序对比去了,但是大体思路是这样)
代码如下:
class Solution {
public static ListNode sortList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode cur=head.next;//后续链表的头节点
ListNode newhead=head;//当前有序链表的头节点
newhead.next=null;//与后续链表断开联系
ListNode prevNext=newhead.next;//有序链表向后遍历的结点
ListNode prev=newhead;//有序链表向后遍历结点的前驱结点
ListNode last=newhead;//尾结点
while(cur!=null) {
//头插
ListNode curNext =cur.next;
if(newhead.val>=cur.val) {
cur.next=newhead;
newhead=cur;
} else if(last.val<cur.val) {
//尾插
last.next=cur;
last=cur;
last.next=null;
} else {//中间插入
//找到大于等于cur.val的结点
while(cur.val>prevNext.val) {
//prev一直保存prevNext的前一个结点
prev=prevNext;
//prevNext置为它的下一个结点
prevNext=prevNext.next;
}
//将cur插入prev和prevNext之间
prev.next=cur;
cur.next=prevNext;
}
//重置prev
prev=newhead;
//重置prevNext
prevNext=prev.next;
//重置cur
cur=curNext;
}
//返回新头节点
return newhead;
}
}
作者总结:
这道题的主要思路就是,将第一个结点单独出来,一步一步和这个链表的后续结点进行对比,分别进行头插,尾插,中间插入,该题的难度并不简单,对于初学者来说。
并且这道题属于经常会考到的面试题,最优的解法可以将时间复杂度缩短到 O(nlogn),后续我在学习归并排序后,会优化该题解。
复杂度分析:
- 时间复杂度O(n^2),n是链表的长度
- 空间复杂度O(1)
删除链表倒数第n个结点oj
删除链表中的重复结点II
删除链表中的节点
重排链表
链表排序