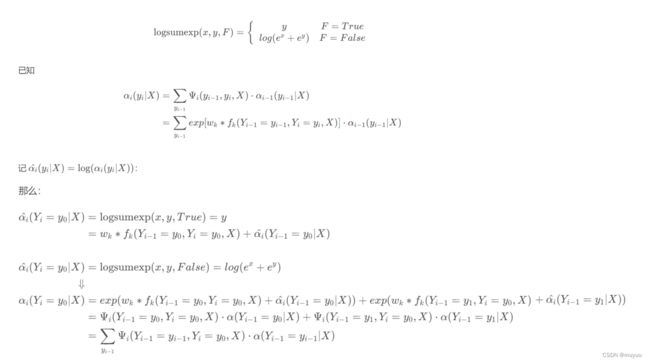CRF++代码解读
目录
- 代码结构
- 特征提取
-
- 数据读入
- 生成特征函数
- 学习过程
-
- 计算loss和gradient
-
- buildLattice
- forwardbackward
- 优化算法 lbgfs
-
- 停止条件
- 预测过程
之前我们在 理论篇 中详细介绍了CRF的公式推理。接下来我们会在这篇里读crf++代码(java版本),并结合理论篇里的公式,完成对整个CRF理论+实践的理解。代码原始版本可以戳crf4j
代码结构
- "CrfLearn"和"CrfTest"分别是学习过程和预测过程的入口。"Encoder"是服务于"CrfLearn"用来执行具体的学习过程。
- "LbfgsOptimizer"是在损失函数和梯度被计算完毕后被"Encoder"调用来进行参数优化,"Mcsrch"是服务于"LbfgsOptimizer"进行步长搜索的函数。
- 剩下的"FeatureIndex, Model, Node, Pair, Tagger, …"都是自定义的数据结构,方便其他功能性函数使用。
特征提取
数据读入
运行"CrfLearn"会直接调用"Encoder"里面的learn函数:
Encoder encoder = new Encoder();
if (!encoder.learn(restArgs[0], restArgs[1], restArgs[2],textmodel, maxiter, freq, eta, C1, C2, threadNum, shrinkingSize, algo, compact)) {
System.err.println("fail to learn model");
return false;
}
learn函数中首先读取了trainFile和templFile,这两个文件的格式都在理论篇中介绍了。
List<TaggerImpl> x = new ArrayList<TaggerImpl>();//用于放所有的train data,按句分开
if (!featureIndex.open(templFile, trainFile)) {//featureIndex用于储存所有与特征函数相关的东西,包括特征模板,特征函数及其id,特征函数的权重,output的label等等,详见EncoderFeatureIndex类
System.err.println("Fail to open " + templFile + " " + trainFile);
}
生成特征函数
接下来对每一句话,定义一个TaggerImpl类的变量tagger,tagger里面存这句话的训练数据以及特征模板信息:
TaggerImpl tagger = new TaggerImpl(TaggerImpl.Mode.LEARN);//tagger用来储存一句训练数据包含的所有内容,详见TaggerImpl类
tagger.open(featureIndex);//tagger里存特征模板信息
TaggerImpl.ReadStatus status = tagger.read(br);//tagger里存训练数据
接下来解析特征函数的入口在这里:
if (!tagger.shrink()) {//遍历模板及数据,将得到的特征,特征的index,以及特征被hit中的次数放到featureIndex.dic_里面去
System.err.println("fail to build feature index ");
return false;
}
进入shrink()函数,立马就调用了buildFeatures(),再进入buildFeatures()函数,可以看到它是分别解析unigram和bigram两类模板生成的特征:
public boolean buildFeatures(TaggerImpl tagger) {//该函数的功能是根据模板提取特征
List<Integer> feature = new ArrayList<Integer>();
List<List<Integer>> featureCache = tagger.getFeatureCache_();
tagger.setFeature_id_(featureCache.size());
//unigram模板一共生成x_.size()*num个特征,x_.size()*num*y_.size()个特征函数,其中num是模板的个数
for (int cur = 0; cur < tagger.size(); cur++) {//一次读tagger里面的一行,例如"Confidence NN B"
if (!buildFeatureFromTempl(feature, unigramTempls_, cur, tagger)) {//根据unigram特征模板,生成该行对应的特征
return false;
}
feature.add(-1);//以-1结尾
featureCache.add(feature);//featureCache[i]用于存放第i行数据根据unigram模板生成的特征(可能不止一个)的起始位置,例如featureCache[0]='0,3,-1',featureCache[1]='6,9,-1'
feature = new ArrayList<Integer>();
}
//从第二个词开始,利用bigram模板生成bigram特征,如果模板是B,那么只生成一个特征,如果是类似B00%x[0,0],那么生成x_.size()-1个特征
for (int cur = 1; cur < tagger.size(); cur++) {
if (!buildFeatureFromTempl(feature, bigramTempls_, cur, tagger)) {
return false;
}
feature.add(-1);
featureCache.add(feature);
feature = new ArrayList<Integer>();
}
return true;
}
解释一下特征模板,特征,特征函数的区别:
- 特征模板形如
U01:%x[0,0]或者B,它是直接在temlpFile里面人工定义的 - 特征是由训练数据遍历特征模板得到的,例如训练数据
Confidence NN B经过特征模板U01:%x[0,0]就会得到特征U01:Confidence;如果经过的特征模板是U08:%x[0,1]就会得到特征U08:NN - 特征函数实际上是由上面的特征展开得到的,如果是unigram特征,就展开成label个特征函数,如果是bigram特征,就展开成label*label个特征函数
上面buildFeatures里最主要的功能都在buildFeatureFromTempl里面,我们再进入到buildFeatureFromTempl函数,主要的功能函数applyRule和getID的作用都在下面注释了,不难看出,虽然理论上我们使用的都是特征函数,但由于特征函数是特征按照一定规律展开出来的,所以为了节省内存,代码里只存了所有的特征及其起始位置:
private boolean buildFeatureFromTempl(List<Integer> feature, List<String> templs, int curPos, TaggerImpl tagger) {
for (String tmpl : templs) {
String featureID = applyRule(tmpl, curPos, tagger);//根据特征模板U00:%x[row,col]生成特征"U00:{tagger.x_[cur+row,col]}",例如第一行是"Confidence NN B"时,U00:%x[0,0]生成特征"U00:Confidence"
if (featureID == null || featureID.length() == 0) {
System.err.println("format error");
return false;
}
int id = getID(featureID);//featureID这个特征的起始位置,每个特征都有y_.size()或者y_.size()^2个特征函数
if (id != -1) {
feature.add(id);
}
}
return true;
}
至此就完成了一个tagger.shrink()并回到"Encoder"里面。接下来给这条数据分配一个线程,并将这句话加到x里面:
tagger.setThread_id_(lineNo % threadNum);//每条数据分配一个thread
x.add(tagger);//x用于放所有的train data,按句分开
以上步骤重复直至所有训练数据都读取完,所有的特征也都解析完毕。下面会经过featureIndex.shrink(freq, x);,用于将出现频率低于freq的特征过滤掉。
学习过程
有了特征函数,我们下面可以按照理论篇 的公式来计算loss func和gradient:
计算loss和gradient
接下来初始化特征函数的参数alpha:
double[] alpha = new double[featureIndex.size()];//alpha的维度为x.size()*y.size()*num,每一个特征函数都有一个权重参数
Arrays.fill(alpha, 0.0);
然后根据选择的模型进行训练:
switch (algo) {
case CRF_L1:
if (!runCRF(x, featureIndex, alpha, maxitr, C1, C2, eta, shrinkingSize, threadNum, true)) {
System.err.println("CRF_L1 execute error");
return false;
}
break;
case CRF_L2:
if (!runCRF(x, featureIndex, alpha, maxitr, C1, C2, eta, shrinkingSize, threadNum, false)) {
System.err.println("CRF_L2 execute error");
return false;
}
break;
case MIRA:
if (!runMIRA(x, featureIndex, alpha, maxitr, C2, eta, shrinkingSize, threadNum)) {
System.err.println("MIRA execute error");
return false;
}
break;
default:
break;
}
进入runCRF(),首先是将各个线程里面计算的loss和gradient累加:
for (int i = 1; i < threadNum; i++) {
threads.get(0).obj += threads.get(i).obj;//累加loss fun的值
threads.get(0).err += threads.get(i).err;//预测错的词数
threads.get(0).zeroone += threads.get(i).zeroone;//预测错的句子数
}
for (int i = 1; i < threadNum; i++) {
for (int k = 0; k < featureIndex.size(); k++) {
threads.get(0).expected[k] += threads.get(i).expected[k];//累加所有training data的梯度
}
}
然后是根据需要,在loss及gradient后面加上正则化的部分:
if (orthant) {
for (int k = 0; k < featureIndex.size(); k++) {//L1正则化
threads.get(0).obj += Math.abs(alpha[k] / C1)
//L1正则化的梯度会根据x所处的位置有不同,因此放到lbfgs里面计算
if (alpha[k] != 0.0) {
numNonZero++;
}
}
} else {
numNonZero = featureIndex.size();
for (int k = 0; k < featureIndex.size(); k++) {//L2正则化
threads.get(0).obj += (alpha[k] * alpha[k] / (2.0 * C2));
threads.get(0).expected[k] += alpha[k] / C2;
}
}
多线程计算loss和gradient是通过调用CRFEncoderThread.java实现的:
for (int i = start_i; i < size; i = i + threadNum) {
obj += x.get(i).gradient(expected);//计算loss和gradient
int errorNum = x.get(i).eval();
x.get(i).clearNodes();
err += errorNum;//预测错的词数
if (errorNum != 0) {
++zeroone;//预测错的句子数
}
}
buildLattice
主要的功能在gradient()里实现:
public double gradient(double[] expected) {
if (x_.isEmpty()) {
return 0.0;
}
buildLattice();//计算所有node和path上的loss,也就是unigram和bigram的loss,对应公式(3.1)里面的w_kf_k(X,Y)
forwardbackward();//利用前向后向算法计算alpha和beta,并计算归一化因子Z_w
double s = 0.0;
for (int i = 0; i < x_.size(); i++) {
for (int j = 0; j < ysize_; j++) {
node_.get(i).get(j).calcExpectation(expected, Z_, ysize_);//计算公式(3.3)梯度项里面的E_p(f)
}
}
for (int i = 0; i < x_.size(); i++) {
List<Integer> fvector = node_.get(i).get(answer_.get(i)).fVector;//answer_[i]表示第i个词的真实label, 取(i,label)对应的unigram特征
for (int j = 0; fvector.get(j) != -1; j++) {//遍历(i,label)对应的unigram特征
int idx = fvector.get(j) + answer_.get(i);//找到unigram特征的index
expected[idx]--;//每遍历一个unigram特征,就减1,遍历所有的特征之后,就相当于减掉了公式(3.2)中f(Y,X)的unigram部分
}
s += node_.get(i).get(answer_.get(i)).cost; //UNIGRAM COST
List<Path> lpath = node_.get(i).get(answer_.get(i)).lpath;//answer_[i]表示第i个词的真实label,取(i,label)对应的bigram特征
for (Path p : lpath) {//遍历(i,label)对应的bigram特征
if (p.lnode.y == answer_.get(p.lnode.x)) {
for (int k = 0; p.fvector.get(k) != -1; k++) {
int idx = p.fvector.get(k) + p.lnode.y * ysize_ + p.rnode.y;//找到bigram特征的index
expected[idx]--;//同上,相当于剪掉了公式(3.2)中的f(X,Y)的bigram部分
}
s += p.cost; // BIGRAM COST
break;
}
}
}
viterbi();//用上一个iter更新得到的参数alpha来对当前的句子进行预测,并记录预测结果到result_里面
return Z_ - s;//s是公式(3.1)中的\sum w_k*f_k
}
gradient()里首先调用buildLattice()来计算 理论篇 里公式(3.1)中的 ∑ w k f k ( X , Y ) \sum w_kf_k(X,Y) ∑wkfk(X,Y):
public void buildLattice() {
if (!x_.isEmpty()) {
feature_index_.rebuildFeatures(this);//创建节点,以及节点之间的边,一共x_.size()*y_.size()个节点
for (int i = 0; i < x_.size(); i++) {
for (int j = 0; j < ysize_; j++) {
feature_index_.calcCost(node_.get(i).get(j));//计算节点(i,j)上的loss,也就是(i,j)对应的所有unigram loss
List<Path> lpath = node_.get(i).get(j).lpath;
for (Path p : lpath) {//从第二个节点开始,每个节点有y_.size()条lpath
feature_index_.calcCost(p);//计算边的loss,也就是点(i,j)上的所有bigram loss
}
}
}
首先rebuildFeatures里面构建了一个有x_.size()*y_.size()个node的lattice网络,其中x_.size()是这句话的长度,y_.size()是label的个数。因为每一个词的label都有label_num种可能,所以这样一个lattice可以囊括一句话所有可能的标注。因为lattice是全连接的,所有一共有y_.size() ∗ * ∗ y_.size() ∗ * ∗ (x_.size()-1)条path:
public void rebuildFeatures(TaggerImpl tagger) {
int fid = tagger.getFeature_id_();
List<List<Integer>> featureCache = tagger.getFeatureCache_();
//遍历每个词及所有可能的label,生成x_.size()*y_.size()个节点
for (int cur = 0; cur < tagger.size(); cur++) {//遍历每个词
List<Integer> f = featureCache.get(fid++);//取出第cur个词对应的特征的index,例如[0,3,-1]表示这个词对应了两个unigram特征,起始位置分别为0和3
for (int i = 0; i < y_.size(); i++) {
Node n = new Node();
n.clear();
n.x = cur;//当前词的位置
n.y = i;//当前词的label,(x,y)表示第x个词的label为y的节点
n.fVector = f;//cur词对应的特征的index,只用fVector就可以找到相应特征,再加上label值,就是一个特征函数
tagger.set_node(n, cur, i);//对tagger.node_[cur][i]赋值Node n
}
}
//从第二个词开始构造节点之间的边,两个词之间有y_.size()*y_.size()条边
for (int cur = 1; cur < tagger.size(); cur++) {//从第二个词开始遍历
List<Integer> f = featureCache.get(fid++);
for (int j = 0; j < y_.size(); j++) {
for (int i = 0; i < y_.size(); i++) {
Path p = new Path();
p.clear();
//下面的p.add实际会更新node_里面的各个节点的lpath和rpath,每个节点有y_.size()个lpath和y_.size()个rpath
p.add(tagger.node(cur - 1, j), tagger.node(cur, i));//将节点(cur-1,j)添加为p的左节点,将节点(cur, i)添加为p的右节点,并将p加为节点(cur-1,j)的右边,节点(cur, i)的左边
// 即p是节点(cur-1,j)和(cur, i)间的边
p.fvector = f;//bigram特征的index
}
}
}
}
从rebuildFeatures出来之后,接下来会调用calcCost来分别计算node和path上的loss值:
public void calcCost(Node node) {//计算节点上的cost,也就是公式(3.1)里w_kf_k(X,Y)中对应unigram特征函数的部分
node.cost = 0.0;
if (alphaFloat_ != null) {
float c = 0.0f;
for (int i = 0; node.fVector.get(i) != -1; i++) {
c += alphaFloat_[node.fVector.get(i) + node.y];
}
node.cost = costFactor_ * c;
} else {
double c = 0.0;
for (int i = 0; node.fVector.get(i) != -1; i++) {//node_i的fVector储存的是第i个词对应的uni特征的index,因此这里是遍历第i行的词的uni特征,一般有几个uni模板,每个词就有几个uni特征
c += alpha_[node.fVector.get(i) + node.y];//每一个特征函数的值都是1,而alpha_[node.fVector.get(i) + node.y]是对应特征函数的权值,这里省略了*1
//因为node.fVector.get(i)只是特征的起始位置,还需要再加上n.y才能定位到形如f('U00:Confidence',y='label')的完整特征函数
//c是这个节点上所有unigram loss的累加
}
node.cost = costFactor_ * c;//将c赋值给node.cost,即node[i][j].cost等于公式(1.1)中的u(y_i=j,X,i)
}
}
可以看出在node上调用calcCost其实就遍历一行输入生成的所有unigram模板(可以从node.fVector得到),然后根据这个词的label是什么(这里用y来指代这个词的label在label列表里的位置)从而得到一行输入生成的所有unigram特征函数的index,再用这个index到alpha列表(也就是理论篇里用的 w k w_k wk)里面去做索引并且乘以 f k ( X , Y ) f_k(X,Y) fk(X,Y)(因为 f k ( X , Y ) = 1 f_k(X,Y)=1 fk(X,Y)=1所以代码里省略了)。将以上全部叠加,得到的就是这行输入生成的所有unigram特征函数对loss的贡献。
rebuildFeatures里面并没有更新参数alpha,参数alpha是每一个iter在lbfgs里面更新的,所以calcCost里用到的alpha是上一个iter里lbfgs更新出来的
calcCost在path上的计算过程跟node类似,主要区别是计算path对应的是bigram特征,所以找所有bigram特征函数的index的时候有点不同:
for (int i = 0; path.fvector.get(i) != -1; i++) {
c += alpha_[path.fvector.get(i) + path.lnode.y * y_.size() + path.rnode.y];//特征函数的值都为1,乘上权值alpha_[path.fvector.get(i) + path.lnode.y * y_.size() + path.rnode.y]
//bigram特征的起始位置在path.fvector.get(i),因为一个bigram特征可以生成y_.size()*y_.size()个特征函数,所以首先要加上path.lnode.y * y_.size(),再加上path.rnode.y
}
path.cost = costFactor_ * c;//将c赋值给path.cost,path.cost等于公式(1.1)里的b(y_{path.lnode.x}=path.lnode.y, y_{path.rnode.x}=path.rnode.y, X)
forwardbackward
至此我们就解读完了buildLattice()这个函数的功能,下面回到gradient()函数,接下来要做的是forwardbackward(),这个函数就是在实现理论篇里前向算法和后向算法的部分,并且通过前向后向算法计算了归一化因子 Z w Z_w Zw:
public void forwardbackward() {
if (!x_.isEmpty()) {
for (int i = 0; i < x_.size(); i++) {//前向算法,参考公式(3.4)
for (int j = 0; j < ysize_; j++) {
node_.get(i).get(j).calcAlpha();
}
}
for (int i = x_.size() - 1; i >= 0; i--) {//后向算法,参考公式(3.5)
for (int j = 0; j < ysize_; j++) {
node_.get(i).get(j).calcBeta();
}
}
Z_ = 0.0;//计算Z_w
for (int j = 0; j < ysize_; j++) {
Z_ = Node.logsumexp(Z_, node_.get(0).get(j).beta, j == 0);//根据公式(3.6), Z = \beta(1) or \alpha(n)
}
}
}
calcAlpha和calcBeta实现逻辑相同,里面比较特别的地方是用了logsumexp来提高计算稳定性:
public void calcAlpha() {
alpha = 0.0;
for (Path p: lpath) {
alpha = logsumexp(alpha, p.cost + p.lnode.alpha, p == lpath.get(0));//函数里面先取了exp,因此p.cost + p.lnode.alpha 会变成相乘;此处的alpha实际等于log(公式里的alpha)
}
//算alpha的公式(3.4): alpha(i) = \sum phi(y_{i-1},y_i)*alpha(i-1),在log空间里转化为 alpha(i) = \sum (\sum_k w_k*f_k + alpha(i-1))
alpha += cost;//此处的cost就是log(公式中的w_k*f_k)
}
}
到这里就解读完了forwardbackward()这个函数的功能,下面再回到gradient()函数,有了前向后向算法计算得到的结果,接下来就可以调用calcExpectation来计算梯度了,对应的是理论篇里的利用公式(3.7)和(3.8)来计算(3.3):
public void calcExpectation(double[] expected, double Z, int size) {
double c = Math.exp(alpha + beta - cost - Z);//由公式(3.7),P(Y_i=y_i|X) = alpha(i)*beta(i)/Z,映到log空间,P(Y_i=y_i|X) = alpha + beta -Z
// -cost是因为beta里面多加了一个cost,所以要减掉一个
for (int i = 0; fVector.get(i) != -1; i++) {
int idx = fVector.get(i) + y;
expected[idx] += c;//expect是公式(3.3)中的E_{P}(f_k),这个位置加的是当f_k为unigram特征时的项
}
for (Path p: lpath) {
p.calcExpectation(expected, Z, size);//公式(3.8)
}
}
p.calcExpectation对应的是公式(3.8):
public void calcExpectation(double[] expected, double Z, int size) {
double c = Math.exp(lnode.alpha + cost + rnode.beta - Z);//对应公式(3.8),log空间中乘法变加法
for (int i = 0; fvector.get(i) != -1; i++) {
int idx = fvector.get(i) + lnode.y * size + rnode.y;
expected[idx] += c;//expect是(3.3)中的E_p(f),这个位置加的是当f_k是bigram时的项
}
}
到这里为止我们已经计算了loss [公式(3.1)]中的 l o g Z w log Z_w logZw以及gradient [公式(3.3)]中的 ∑ i = 1 n [ ∑ y i , y i − 1 f k ( Y i − 1 = y i − 1 , Y i = y i , X , i ) P ( Y ′ , Y i − 1 = y i − 1 , Y i = y i ∣ X ) + ∑ y i f k ( Y i = y i , X , i ) P ( Y ′ , Y i = y i ∣ X ) ] \sum_{i=1}^n[\sum_{y_i,y_{i-1}}f_k(Y_{i-1}=y_{i-1},Y_i=y_i,X,i)P(Y',Y_{i-1}=y_{i-1},Y_i=y_i|X) + \sum_{y_i}f_k(Y_i=y_i,X,i)P(Y',Y_i=y_i|X)] ∑i=1n[∑yi,yi−1fk(Yi−1=yi−1,Yi=yi,X,i)P(Y′,Yi−1=yi−1,Yi=yi∣X)+∑yifk(Yi=yi,X,i)P(Y′,Yi=yi∣X)],所以为了计算得到完整的loss和gradient,我们还分别需要计算 − ∑ k = 1 K w k f k ( X , Y ) -\sum_{k=1}^Kw_k f_k(X,Y) −∑k=1Kwkfk(X,Y)和 − f k ( Y , X ) -f_k(Y,X) −fk(Y,X):
for (int i = 0; i < x_.size(); i++) {
List<Integer> fvector = node_.get(i).get(answer_.get(i)).fVector;//answer_[i]表示第i个词的真实label, 取(i,label)对应的unigram特征
for (int j = 0; fvector.get(j) != -1; j++) {//遍历(i,label)对应的unigram特征
int idx = fvector.get(j) + answer_.get(i);//找到unigram特征的index
expected[idx]--;//每遍历一个unigram特征,就减1,遍历所有的特征之后,就相当于减掉了公式(3.2)中f(Y,X)的unigram部分
}
s += node_.get(i).get(answer_.get(i)).cost; //UNIGRAM COST
List<Path> lpath = node_.get(i).get(answer_.get(i)).lpath;//answer_[i]表示第i个词的真实label,取(i,label)对应的bigram特征
for (Path p : lpath) {//遍历(i,label)对应的bigram特征
if (p.lnode.y == answer_.get(p.lnode.x)) {
for (int k = 0; p.fvector.get(k) != -1; k++) {
int idx = p.fvector.get(k) + p.lnode.y * ysize_ + p.rnode.y;//找到bigram特征的index
expected[idx]--;//同上,相当于剪掉了公式(3.2)中的f(X,Y)的bigram部分
}
s += p.cost; // BIGRAM COST
break;
}
}
}
viterbi();
return Z_ - s;//s是公式(3.1)中的\sum w_k*f_k
上面的viterbi()是用上一个iter更新得到的参数alpha来对当前的句子进行预测,并记录预测结果到result_里面。
至此整个gradient()的功能都运行完了一遍,不过这只是针对一句话的,所有训练数据里的句子都做完这个流程(当然可以多线程进行)之后累加就得到了所有训练数据的loss和gradient。再加上前面说的正则化项,下面我们将所有的东西丢到lbfgs.optimize里去优化:
int ret = lbfgs.optimize(featureIndex.size(), alpha, threads.get(0).obj, threads.get(0).expected, orthant, C1, C2);
这个函数的主要功能就是利用优化算法lbfgs来更新参数alpha。
优化算法 lbgfs
lbfgs的理论推导请戳数值优化-lbfgs,代码解读如下:
package com.github.zhifac.crf4j;
import java.util.Arrays;
import java.util.List;
/**
* Quasi-Newton optimizer
*
* This section implement the quasi-Newton optimizer. We use the L-BFGS
* algorithm described by Liu and Nocedal in [1] and [2]. If an l1-norm must
* be applyed we fallback on the OWL-QN variant described in [3] by Galen and
* Jianfeng which allow to use L-BFGS for function not differentiable in 0.0.
*
* [1] Updating quasi-Newton matrices with limited storage, Jorge Nocedal, in
* Mathematics of Computation, vol. 35(151) 773-782, July 1980.
* [2] On the limited memory BFGS method for large scale optimization, Dong C.
* Liu and Jorge Nocedal, in Mathematical Programming, vol. 45(1) 503-528,
* January 1989.
* [3] Scalable Training of L1-Regularized Log-Linear Models, Andrew Galen and
* Gao Jianfeng, in Proceedings of the 24th International Conference on
* Machine Learning (ICML), Corvallis, OR, 2007.
**/
public class LbfgsOptimizer {
int iflag_, iscn, nfev, iycn, point, npt, iter, info, ispt, isyt, iypt, maxfev;
double stp, stp1;
double[] diag_ = null;
double[] w_ = null;
double[] v_ = null;
double[] xi_ = null;
Mcsrch mcsrch_ = null;
// Compute the pseudo-gradient of crf-l1 for owl-qn. It is
// defined in [3, pp 335(4)]
// | ∂_i^- f(x) if ∂_i^- f(x) > 0
// ◇_i f(x) = | ∂_i^+ f(x) if ∂_i^+ f(x) < 0
// | 0 otherwise
// with
// ∂_i^± f(x) = ∂/∂x_i l(x) + | Cσ(x_i) if x_i ≠ 0
// | ±C if x_i = 0
public void pseudo_gradient(int size,
double[] v,//pseudo_gradient
double[] x,
double[] g,
double C) {
for (int i = 0; i < size; ++i) {
if (x[i] == 0) {
if (g[i] + C < 0) {
v[i] = g[i] + C;
} else if (g[i] - C > 0) {
v[i] = g[i] - C;
} else {
v[i] = 0;
}
} else {
v[i] = g[i] + C * Mcsrch.sigma(x[i]);
}
}
}
//参考[1,pp 779]中的迭代计算H*g的recursive formula:
//Loop1: q = f'(x)
// alpah = rho * s^T * q
// q = q - alpha * y
//Loop2: r_0 = H_0 q_0
// beta = rho * y^T * r
// r = r + s(alpha - beta)
int lbfgs_optimize(int size,//权重向量的长度
int msize,//lbfgs超参,只保存msize个向量来计算H*g
double[] x,//feature的权重
double f, //obj的值
double[] g, //crf loss的梯度
double[] diag,//[2, pp 515]定义的H_0,也就是[1, pp 779]double loop循环中的H_0
double[] w,//存放最近m个rho,y,s; 以及计算搜索方向时的临时变量alpha,q,r等
boolean orthant, //true when crf-l1, false when crf-l2
double C1,
double C2,
double[] v,//crf-l2:v=g;crf-l1,v is pseudo_gradient
double[] xi,//crf-l1时存放x的符号
int iflag) {
double yy = 0.0;
double ys = 0.0;
int bound = 0;
int cp = 0;
if (orthant) {
pseudo_gradient(size, v, x, g, C1);//v is pseudo_gradient for crf-l1
}
if (mcsrch_ == null) {
mcsrch_ = new Mcsrch();
}
boolean firstLoop = true;
// initialization
if (iflag == 0) {
point = 0;
// r_0 = H_0 q_0
// Scaling is described in [2, pp 515]
// for k = 0: H_0 = I
for (int i = 0; i < size; ++i) {
diag[i] = 1.0;
}
//w[1:size]存放lbfgs迭代时的临时变量q或r; 在计算出line search搜索方向后,w[1:size]也用来存放梯度f'(x),
//以便后面确定好步长后,来计算梯度变化(w[iypt + npt + i] = g[i] - w[i];)
// 注意每次传进来的g可能不是f'(x_k),也有可能是f'(x+stp*r)
//
//w[size + 1 : size + m] 存放rho
//w[size + m + 1 : size + 2*m] 存放alpha(双loop循环中的临时变量)
//w[size+2*m+1 : size+2*m+m*size]用于存放[1, pp 773]上定义的s,可以保存最近的m个s
//w[size+2*m+m*size+1 : size+2*m+m*size+m*size]用于存放[1, pp 773]上定义的y,可以保存最近的m个y
ispt = size + (msize << 1);//存放m个s的下标基址
iypt = ispt + size * msize;//存放m个y的下标基址
//r_0 = H_0 q_0,第一次迭代的搜索方向
for (int i = 0; i < size; ++i) {
w[ispt + i] = -v[i] * diag[i];
}
stp1 = 1.0 / Math.sqrt(Mcsrch.ddot_(size, v, 0, v, 0));
}
// Double Loop Algo described in [1, pp 779]
while (true) {
if (!firstLoop || (firstLoop && iflag != 1 && iflag != 2)) {
++iter;
info = 0;
if (orthant) {//crf-l1,用于后面line search时限制在一个象限内
for (int i = 0; i < size; ++i) {
xi[i] = (x[i] != 0 ? Mcsrch.sigma(x[i]) : Mcsrch.sigma(-v[i]));
}
}
if (iter != 1) {
if (iter > size) bound = size;
// r_0 = H_0 q_0
// Scaling is described in [2, pp 515]
// for k > 0: H_0 = I * y_k^T s_k / ||y_k||²
ys = Mcsrch.ddot_(size, w, iypt + npt, w, ispt + npt);//y_k^T s_k
yy = Mcsrch.ddot_(size, w, iypt + npt, w, iypt + npt);//||y_k||²
for (int i = 0; i < size; ++i) {
diag[i] = ys / yy;//H_0 = I * y_k^T s_k / ||y_k||²
}
}
}
if (iter != 1 && (!firstLoop || (iflag != 1 && firstLoop))) {
cp = point;
if (point == 0) {
cp = msize;
}
//w[size+1:size+m]存放[1, pp 774]上定义的rho = 1/y^T s
w[size + cp - 1] = 1.0 / ys;
//初始化w[1:size]为-g
for (int i = 0; i < size; ++i) {
w[i] = -v[i];
}
bound = Math.min(iter - 1, msize);//即[1, pp 779]上Recursive Formula里面定义的BOUND
cp = point;
for (int i = 0; i < bound; ++i) {
--cp;
if (cp == -1) {
cp = msize - 1;
}
//下面计算First Loop里的 alpha = rho * s^T * q
// sq = s^T * q
double sq = Mcsrch.ddot_(size, w, ispt + cp * size, w, 0);
int inmc = size + msize + cp;
iycn = iypt + cp * size;//定位y的起始位置
w[inmc] = w[size + cp] * sq;//w[inmc]用于存放alpha = rho * s^T * q
double d = -w[inmc];
//下面计算First Loop里的q = q - alpha * y
Mcsrch.daxpy_(size, d, w, iycn, w, 0);//w[1:size]里存放累加得到的q_0
}
//Second Loop中的初始化 r_0 = H_0*q_0
for (int i = 0; i < size; ++i) {
w[i] = diag[i] * w[i];//此时w[1:size]里存放的是q_0
}
for (int i = 0; i < bound; ++i) {
//下面计算Second Loop里的 beta = rho * y^T * r
//yr = y^T * r
double yr = Mcsrch.ddot_(size, w, iypt + cp * size, w, 0);
double beta = w[size + cp] * yr;// beta = rho * y^T * r
int inmc = size + msize + cp;
beta = w[inmc] - beta;// w[inmc]此时放的是FirstLoop里计算得到的alpha,beta更新为 beta - alpha
iscn = ispt + cp * size;//定位s的起始位置
//下面计算Second Loop里的 r = r + s(alpha-beta)
Mcsrch.daxpy_(size, beta, w, iscn, w, 0);//w[1:size]里存放累加得到的r_last,也就是下降方向
++cp;
if (cp == msize) {
cp = 0;
}
}
if (orthant) {//crf-l1, 校正搜索方向,以使搜索方向不与伪梯度相反
for (int i = 0; i < size; ++i) {
w[i] = (Mcsrch.sigma(w[i]) == Mcsrch.sigma(-v[i]) ? w[i] : 0);
}
}
// STORE THE NEW SEARCH DIRECTION
//将w[1:size]此时存放的下降方向r存放到w[ispt + point * size : ispt + point * size + size]
for (int i = 0; i < size; ++i) {
w[ispt + point * size + i] = w[i];
}
}
// OBTAIN THE ONE-DIMENSIONAL MINIMIZER OF THE FUNCTION
// BY USING THE LINE SEARCH ROUTINE MCSRCH
if (!firstLoop || (firstLoop && iflag != 1)) {
nfev = 0;//nfev表示mcsrch评估函数值和梯度的次数,每评估一次mcsrch里面就会加1,达到最大搜索次数后认为搜索失败,crf主程序也会退出
stp = 1.0;
if (iter == 1) {
stp = stp1;
}
for (int i = 0; i < size; ++i) {
w[i] = g[i];//储存梯度f'(x),后面用于计算梯度变换f'(x+stp*r) - f'(x)
}
}
double[] stpArr = {stp};
int[] infoArr = {info};
int[] nfevArr = {nfev};
//mcsrch中寻找满足Wolfe condition的步长,并输出到stp里面
mcsrch_.mcsrch(size, x, f, v, w, ispt + point * size,
stpArr, infoArr, nfevArr, diag);
stp = stpArr[0];
info = infoArr[0];
nfev = nfevArr[0];
if (info == -1) {
if (orthant) {//crf-l1: 限制line search搜索的一系列点都在指定象限
for (int i = 0; i < size; ++i) {
x[i] = (Mcsrch.sigma(x[i]) == Mcsrch.sigma(xi[i]) ? x[i] : 0);
}
}
return 1; // next value
}
if (info != 1) {//line search失败,详见mcsrch里的注释
System.err.println("The line search routine mcsrch failed: error code:" + info);
return -1;
}
//找到了满足Wolfe condition的步长stp
npt = point * size;
for (int i = 0; i < size; ++i) {
w[ispt + npt + i] = stp * w[ispt + npt + i];//w[ispt + npt + i]重新储存为下降方向r*stp
w[iypt + npt + i] = g[i] - w[i];//g[i]在mcsrh中被重新计算为f'(x + stp*r)
//因此w[iypt + npt + i]中存放的是f'(x + stp*r) - f'(x)
}
++point;
if (point == msize) point = 0;
double gnorm = Math.sqrt(Mcsrch.ddot_(size, v, 0, v, 0));
double xnorm = Math.max(1.0, Math.sqrt(Mcsrch.ddot_(size, x, 0, x, 0)));
if (gnorm / xnorm <= Mcsrch.eps) {//梯度足够小就停止
return 0; // OK terminated
}
firstLoop = false;
}
}
public LbfgsOptimizer() {
iflag_ = iscn = nfev = 0;
iycn = point = npt = iter = info = ispt = isyt = iypt = maxfev = 0;
mcsrch_ = null;
}
public void clear() {
iflag_ = iscn = nfev = iycn = point = npt =
iter = info = ispt = isyt = iypt = 0;
stp = stp1 = 0.0;
diag_ = null;
w_ = null;
v_ = null;
mcsrch_ = null;
}
public int init(int n, int m) {
//This is old interface for backword compatibility
final int msize = 5;
final int size = n;
iflag_ = 0;
w_ = new double[size * (2 * msize + 1) + 2 * msize];
Arrays.fill(w_, 0.0);
diag_ = new double[size];
v_ = new double[size];
return 0;
}
public int optimize(double[] x, double f, double[] g) {
return optimize(diag_.length, x, f, g, false, 1.0, 1.0);
}
public int optimize(int size, double[] x, double f, double[] g, boolean orthant, double C1, double C2) {
int msize = 5;
if (w_ == null) {
iflag_ = 0;
w_ = new double[size * (2 * msize + 1) + 2 * msize];
Arrays.fill(w_, 0.0);
diag_ = new double[size];
v_ = new double[size];
if (orthant) {
xi_ = new double[size];
}
} else if (diag_.length != size || v_.length != size) {
System.err.println("size of array is different");
return -1;
} else if (orthant && v_.length != size) {
System.err.println("size of array is different");
return -1;
}
int iflag = 0;
if (orthant) {
iflag = lbfgs_optimize(size,
msize, x, f, g, diag_, w_, orthant, C1, C2, v_, xi_, iflag_);
iflag_ = iflag;
} else {
iflag = lbfgs_optimize(size,
msize, x, f, g, diag_, w_, orthant, C1, C2, g, xi_, iflag_);
iflag_ = iflag;
}
if (iflag < 0) {
System.err.println("routine stops with unexpected error");
return -1;
}
if (iflag == 0) {
clear();
return 0; // terminate
}
return 1; // evaluate next f and g
}
}
停止条件
模型的停止条件代码里设置为:
if (diff < eta) {
converge++;
} else {
converge = 0;
}
if (itr > maxItr || converge == 3) {
break;
}
其中diff是两次迭代loss的相对误差,所有要求两次迭代loss的相对误差连续三次满足小于eta,或者达到最大训练次数。
以上就是全部的学习过程,下面我们解读预测过程的代码。
预测过程
模型预测的入口是CrfTest.java,首先读取model:
FileInputStream stream = new FileInputStream(model);
if (!tagger.open(stream, nbest, vlevel, costFactor)) {//读取model.m里面的值,包括权值参数的值,uni/bigram模板,label的值等
System.err.println("open error");
return false;
}
然后读取testFile数据并用model预测每句话的结果:
TaggerImpl.ReadStatus status = tagger.read(br);//将test data读取,主要是读入x_,创建node,但node里all elements are null;answer_和result_初始化为0
if (TaggerImpl.ReadStatus.ERROR == status) {
System.err.println("read error");
return false;
} else if (TaggerImpl.ReadStatus.EOF == status && tagger.empty()) {
break;
}
if (!tagger.parse()) {//对于输入的一句test data,预测其每个词的label,预测结果放在result_里面
System.err.println("parse error");
return false;
}
模型预测函数parse()的结构如下:
public boolean parse() {//parse函数用于预测
if (!feature_index_.buildFeatures(this)) {//根据一句test data,生成它每个词对应的uni/bigram特征以及特征的index
System.err.println("fail to build featureIndex");
return false;
}
if (x_.isEmpty()) {
return true;
}
buildLattice();//构建node和path,其上的cost分别为公式(1.1)里的u(*)和b(*)
if (nbest_ != 0 || vlevel_ >= 1) {
forwardbackward();
}
viterbi();//用维特比算法做预测
if (nbest_ != 0) {
initNbest();
}
return true;
}
首先是调用buildFeatures解析testFile生成的所有特征;然后是调用buildLattice构建测试数据的node和path;接下来是调用forwardbackward做前向后向算法计算;这些函数都跟学习过程里用到的一样,唯一的区别在于学习过程里用到的参数alpha是上一个iter里更新得到的,而这里用的参数alpha是从model里读取的。如果test data中有train data中不存在的特征,那么这种特征在计算中不会使用,也可以看作权重设为零。
尽管CrfTest里面使用的
buildFeatures()跟CrfLearn里是一样的,但是buildFeatures()里用到的getID()函数是不一样的,CrfLearn里面的getID()函数是根据特征展开的长度来记录这个特征起始位置,而CrfTest里面的getID()函数是在从model里读取的参数里面做查找,并返回找到的index
有了上面的处理,现在就可以用viterbi方法进行预测了:
public void viterbi() {
for (int i = 0; i < x_.size(); i++) {
for (int j = 0; j < ysize_; j++) {
double bestc = -1e37;
Node best = null;
List<Path> lpath = node_.get(i).get(j).lpath;//(i,j)节点的lpath
for (Path p : lpath) {
//path.lnode.bestCost记录的是到path.lnode的最佳路径的score + 路径p的cost(即b(*)) + 节点(i,j)的cost(即u(*))。相当于公式(4.2)花括号里面的内容
double cost = p.lnode.bestCost + p.cost + node_.get(i).get(j).cost;
if (cost > bestc) {
bestc = cost;//更新bestc为到node[i][j]的最佳路径的score,相当于公式(4.2)里面取max的部分
best = p.lnode;//用来记录到节点node[i][j]的最佳路径y_1,...y_{i-1}里的点y_{i-1}是哪个node
}
}
node_.get(i).get(j).prev = best;//prev用来记录到node[i][j]的最佳路径y_1,...y_{i-1}里的点y_{i-1}是哪个node
node_.get(i).get(j).bestCost = best != null ? bestc : node_.get(i).get(j).cost;//将node(i,j)为终点的最佳路径的score保存在bestCost里面
}
}
double bestc = -1e37;
Node best = null;
int s = x_.size() - 1;//到最后一个词
for (int j = 0; j < ysize_; j++) {//遍历最后一个词的ysize_个可能的label
if (bestc < node_.get(s).get(j).bestCost) {
best = node_.get(s).get(j);//best用来记录终点为最后一个词的最佳路径的最后一个节点
bestc = node_.get(s).get(j).bestCost;//bestc记录终点为最后一个词的最佳路径的score
}
}
for (Node n = best; n != null; n = n.prev) {
result_.set(n.x, n.y);//result_用来记录每个词的预测label
}
cost_ = -node_.get(x_.size() - 1).get(result_.get(x_.size() - 1)).bestCost;//记录最佳序列的score
}
通过在lattice里面不断后移node并更新每个node的prev和bestCost参数,当走到最后一个node时,即可以找到最佳路线。其中某个node的bestCost是以该node为最后节点的路径的得分。
至此我们就完成了CrfTest。以上就是整个crf++代码(java版本)的解读。
Reference:
条件随机场之CRF++源码详解-特征