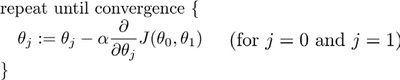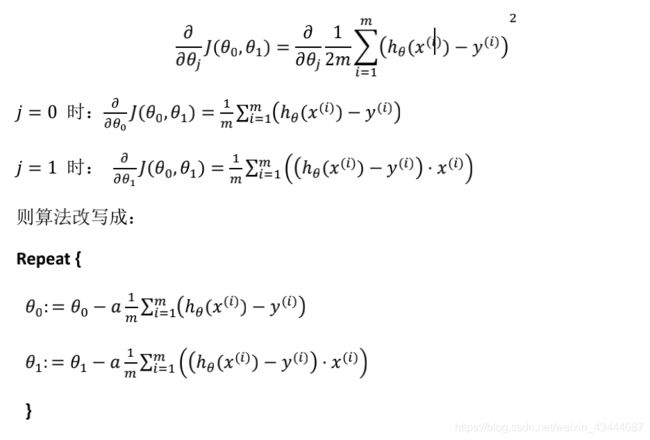吴恩达机器学习1——单变量线性回归、梯度下降

吴恩达机器学习第一周

一、什么是机器学习？

• Arthur Samuel 定义：使计算机无需明确编程即可学习的学习领域

• Tom Mitchell 定义：如果某计算机程序在T任务中的性能（由P衡量）随着经验E的提高而提高，则可以说它是从经验E中学习有关某类任务T和性能度量P的机器学习方法。

  例如：在玩跳棋的任务中。E =玩过许多跳棋游戏的经验、T =扮演跳棋的任务、P =程序将赢得下一场比赛的概率。

二、机器学习的分类

• 机器学习问题通常分为两类，一类是监督学习（Supervised learning），一类是非监督学习（Unsupervised learning）。监督学习这个想法是指，我们将教计算机如何去完成任务，而在无监督学习中，我们打算让它自己进行学习。

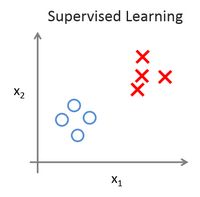
1. 监督学习

• ***监督学习***指的就是我们给学习算法一个数据集。这个数据集由“正确答案”组成，也就是说已经做好了标记。监督学习问题又分为“回归”和“分类”问题。在回归问题中，我们试图预测连续输出中的结果，这意味着我们试图将输入变量映射到某个连续函数。在分类问题中，我们改为尝试预测离散输出的结果。换句话说，我们正在尝试将输入变量映射为离散类别。

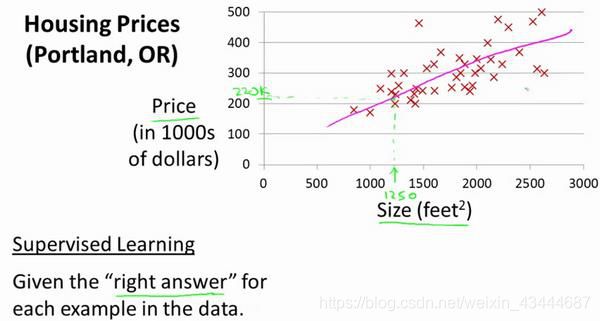
• ***回归问题：***在房价的例子中，我们给了一系列房子的数据，我们给定数据集中每个样本的正确价格，即它们实际的售价然后运用学习算法，算出更多的正确答案。比如你朋友那个新房子的价格。用术语来讲，这叫做回归问题。我们试着推测出一个连续值的结果，即房子的价格。
  

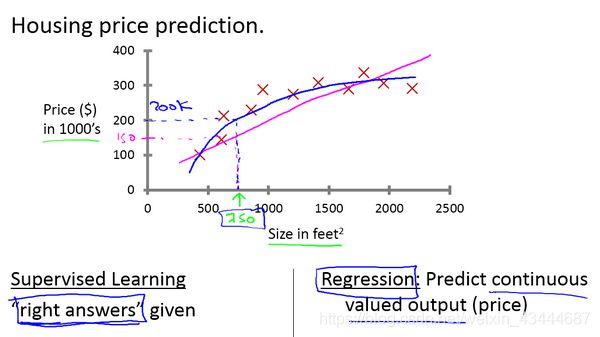
在上图中我们将面积和价格的坐标记录在图像坐标系中，我们想方设法拟合出一条类似于红色的线，再将新房子的面积带入直线中求解价格。为了更加精确，我们还可以应用二次方程来拟合

• 分类问题，比如说我有5个良性肿瘤样本，在1的位置有5个恶性肿瘤样本。现在我们有一个朋友很不幸检查出乳腺肿瘤。假设说她的肿瘤大概这么大，那么机器学习的问题就在于，你能否估算出肿瘤是恶性的或是良性的概率。用术语来讲，这是一个分类问题。
  

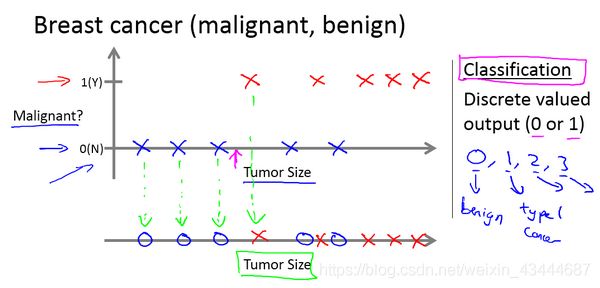
• 假设你经营着一家公司，你想开发学习算法来处理这两个问题：

  你有一大批同样的货物，想象一下，你有上千件一模一样的货物等待出售，这时你想预测接下来的三个月能卖多少件？
  你有许多客户，这时你想写一个软件来检验每一个用户的账户。对于每一个账户，你要判断它们是否曾经被盗过？
  那这两个问题，它们属于分类问题、还是回归问题?

  １．问题一是一个回归问题，因为你知道，如果我有数千件货物，我会把它看成一个实数，一个连续的值。因此卖出的物品数，也是一个连续的值。

  ２．问题二是一个分类问题，因为我会把预测的值，用 0 来表示账户未被盗，用 1 表示账户曾经被盗过。所以我们根据账号是否被盗过，把它们定为0 或 1，然后用算法推测一个账号是 0 还是 1，因为只有少数的离散值，所以我把它归为分类问题。

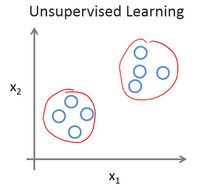
2. 非监督学习

在无监督学习中，我们已知的数据。看上去有点不一样，不同于监督学习的数据的样子，即无监督学习中没有任何的标签或者是有相同的标签或者就是没标签。所以我们已知数据集，却不知如何处理，也未告知每个数据点是什么。别的都不知道，就是一个数据集。你能从数据中找到某种结构吗？针对数据集，无监督学习就能判断出数据有两个不同的聚集簇。这是一个，那是另一个，二者不同。是的，无监督学习算法可能会把这些数据分成两个不同的簇。所以叫做***聚类算法***。

无监督学习，它是学习策略，交给算法大量的数据，并让算法为我们从数据中找出某种结构。

3. 监督学习和非监督学习的举例

• 垃圾邮件问题。如果你有标记好的数据，区别好是垃圾还是非垃圾邮件，我们把这个当作监督学习问题。

• 新闻事件分类的例子，我们看到，可以用一个聚类算法来聚类这些文章到一起，所以是无监督学习。

• 细分市场的例子，你可以当作无监督学习问题，因为我只是拿到算法数据，再让算法去自动地发现细分市场。

• 糖尿病的例子，这个其实就像是我们的乳腺癌。只是替换了好、坏肿瘤，良性、恶性肿瘤，我们改用糖尿病或没病。所以我们把这个当作监督学习，我们能够解决它，作为一个监督学习问题，就像我们在乳腺癌数据中做的一样。

三、单变量线性回归（Linear Regression with One Variable）

1. 模型表示

这里首先给出一个监督学习问题的例子：这里有来自 Portland 地区 47 所房子的面积和 价格数据，通过上述给出的数据，我们是否可利用机器学习来根据房子的面积大小来预测房子价格。

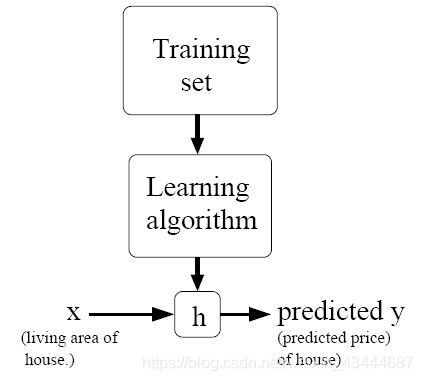
监督学习就是对训练数据给出了正确结果，这里所给出了 47 所房子的真实价格(相对于预测价格来说)就是正确结果。而线性回归就是要根据输入的特征来进行相应的预测。我们将要用来描述这个回归问题的标记如下:

ｍ 代表训练集中实例的数量

x 代表特征/输入变量

y 代表目标变量/输出变量

(x,y) 代表训练集中的样本

(Xi,Yi) 代表第 i 个观察实例

h 代表学习算法的解决方案或函数也称为假设（hypothesis)

2. 代价函数

对于一次线性方程

我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价函数最小

代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。我们之所以要求出误差的平方和，是因为误差平方代价函数，对于大多数问题，特别是回归问题，都是一个合理的选择。还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回归问题最常用的手段了。

代价函数的直观理解

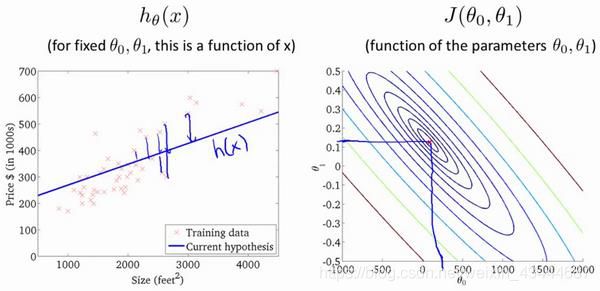
求解流程图：

我们绘制一个等高线图，三个坐标分别为0和1 和(0, 1)：

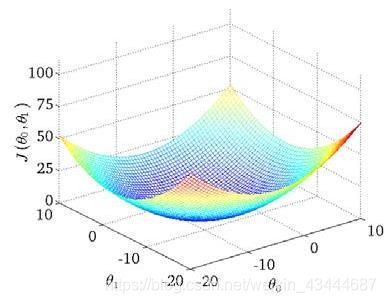
则可以看出在三维空间中存在一个使得(0, 1)最小的点。那个点的坐标就是满足代价函数最小的0和1值。

在右图的等高线图中，每一组点都可以决定一条左图中的一条唯一的一条直线，并且我们可以看到当选择的点越接近中心的红色点时，左侧图像的拟合效果越好。中心点即是我们所求的代价函数最小的0和1值，也可以求出最后的拟合直线。

但这种手动的算法并不是一直有效，当参数过多时可能会失效，所以我们需要一种高效且自动的算法来找出使代价函数取最小值的参数。

3. 梯度下降算法

梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数(0, 1) 的最小值。

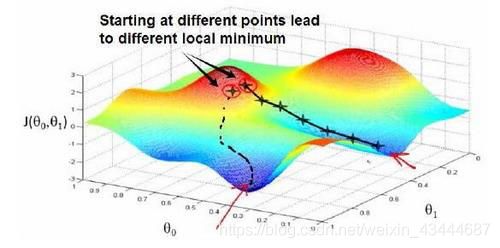
梯度下降背后的思想是：开始时我们随机选择一个参数的组合(0, 1, . . . . . . , )，计算代价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

如图所示，梯度下降算法就是当你处于开始点的时候，不断地向最佳的下山方向走，每一次经过判断走出一步之后，再进行下一次判断。

• 批量梯度下降算法公式为：

其中是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。

在梯度下降算法中，0和1需要同步更新

• 梯度下降的直观理解

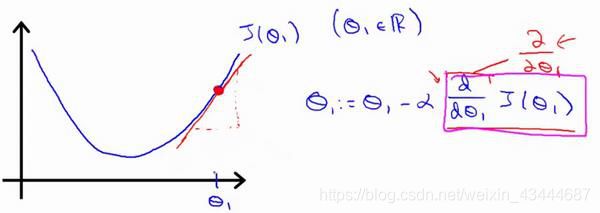
  对赋值，使得()按梯度下降最快方向进行，一直迭代下去，最终得到局部最小值。其中是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。

​ 对于这个问题，求导的目的，基本上可以说取这个红点的切线，就是这样一条红色的直线，刚好与函数相切于这一点，让我们看看这条红色直线的斜率，就是这条刚好与函数曲线相切的这条直线，这条直线的斜率正好是这个三角形的高度除以这个水平长度，现在，这条线有一个正斜率，也就是说它有正导数，因此，我得到的新的1，1更新后等于1减去一个正数乘以。

• a的大小

  • 如果太小了，即我的学习速率太小，结果就是只能一点点地挪动，去努力接近最低点，这样就需要很多步才能到达最低点，所以如果太小的话，可能会很慢，因为它会一点点挪动，它会需要很多步才能到达全局最低点。

  • 如果太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远，所以，如果太大，它会导致无法收敛，甚至发散。

  • 如果你的参数已经处于局部最低点，那么梯度下降法更新其实什么都没做，它不会改变参数的值。

  • 学习速率保持不变时，梯度下降也可以收敛到局部最低点。

4. 梯度下降的线性回归

我们要将梯度下降和代价函数结合。我们将用到此算法，并将其应用于具体的拟合直线的线性回归算法里。

• 梯度下降算法和线性回归算法比较如图：

求解过程：

作业

1. 单变量线性回归

题目描述：在本部分的练习中，您将使用一个变量实现线性回归，以预测食品卡车的利润。假设你是一家餐馆的首席执行官，正在考虑不同的城市开设一个新的分店。该连锁店已经在各个城市拥有卡车，而且你有来自城市的利润和人口数据。
您希望使用这些数据来帮助您选择将哪个城市扩展到下一个城市。

import numpy as np
import matplotlib.pyplot as plt


def compute_cost(X, Y, theta):
    # 两个数组作矩阵乘积
    # 当两个数组的维度不能直接进行矩阵乘法时，dot会把后面的参数进行转置
    hypthesis = np.dot(X, np.transpose(theta))
    # 先转置再做矩阵乘法
    cost = np.dot(np.transpose(hypthesis - Y), (hypthesis - Y))
    cost = cost / (2 * X.shape[0])
    return cost


def gradient_descent(X, Y, theta_init, alpha, iter_num):
    # 样本个数
    m = Y.shape[0]
    # 代价的历史值
    J_history = np.zeros(iter_num)
    theta = theta_init
    # 进行迭代计算
    for num in range(0, iter_num):
        # 计算每一个theta值下的代价值
        J_history[num] = compute_cost(X, Y, theta)
        # 根据公式计算梯度，来更新theta的值
        hyp = np.dot(X, np.transpose(theta))  # x是97，2  theta是1，2  结果是97，1
        theta = theta - alpha * np.dot(np.transpose(hyp - Y), X) / m
    return theta, J_history



# ======== 1.载入数据和绘制散点图 ========
print('读取数据，并绘制散点图...\n')
filepath = r'ex1data1.txt'
# 从文件中读取数据，读取第0列和第1列，要求文件中每一行的列数相等
dataset = np.loadtxt(filepath,
                     delimiter=',',
                     usecols=(0, 1))  # 分隔符 读取第一列和第二列
Xdata = dataset[:, 0]   # 人口数据
Ydata = dataset[:, 1]   # 利润


# ======== 2.计算代价和梯度 ========
print('进行梯度计算...\n')
# 按照第二维度，把两个数组连接起来
# 给输入数据增加一个偏置维度
X = np.c_[np.ones(Xdata.shape[0]), Xdata]
Y = Ydata
# 初始化参数：theta,iter_num,alpha
theta_init = np.zeros(X.shape[1])


iter_num = 12000  # 迭代次数
alpha = 0.01     # 学习速率
# 计算初始代价
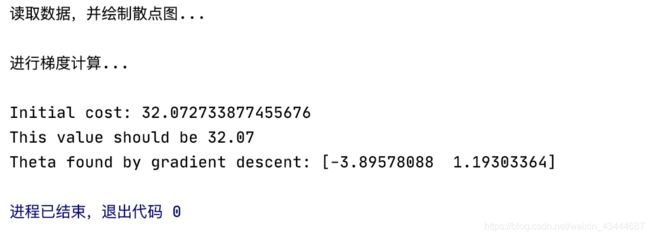
print('Initial cost:',
      str(compute_cost(X, Y, theta_init)),
      '\nThis value should be 32.07')
# 使用梯度下降法进行优化求解
theta_fin, J_history = gradient_descent(X, Y, theta_init, alpha, iter_num)
print('Theta found by gradient descent:', str(theta_fin.reshape(2)))
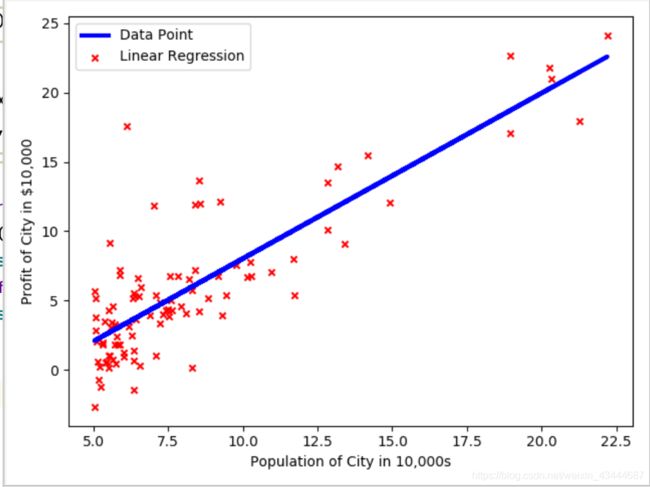
# 绘制数据散点图和线性回归曲线
plt.figure(0)  # 设置图像编号为０
plt.scatter(Xdata, Ydata, c='red', marker='x', s=20)  # 设置图像的参数
plt.plot(X[:, 1], np.dot(X, np.transpose(theta_fin)), 'b-', lw=3)
plt.xlabel('Population of City in 10,000s', fontsize=10)
plt.ylabel('Profit of City in $10,000', fontsize=10)
plt.legend(['Data Point', 'Linear Regression'])
plt.show()

2. 多变量线性回归

在本部分的练习中，需要预测房价，输入变量有两个特征，一是房子的面积，二是房子卧室的数量；输出变量是房子的价格。

import numpy as np
import matplotlib.pyplot as plt

def feature_normalize(Xdata):
    # 计算每一维度的均值
	X_mean = np.mean(Xdata,axis=0)   # 每列均值
	X_std = np.std(Xdata,axis=0)     # 每列标准差
	X_norm = np.divide(np.subtract(Xdata,X_mean),X_std)

	return X_norm,X_mean,X_std

def compute_cost(X, Y, theta):
    # 两个数组作矩阵乘积
    # 当两个数组的维度不能直接进行矩阵乘法时，dot会把后面的参数进行转置
    hypthesis = np.dot(X, np.transpose(theta))
    # 先转置再做矩阵乘法
    cost = np.dot(np.transpose(hypthesis - Y), (hypthesis - Y))
    cost = cost / (2 * X.shape[0])
    return cost


def gradient_descent(X, Y, theta_init, alpha, iter_num):
    # 样本个数
    m = Y.shape[0]
    # 代价的历史值
    J_history = np.zeros(iter_num)
    theta = theta_init
    # 进行迭代计算
    for num in range(0, iter_num):
        # 计算每一个theta值下的代价值
        J_history[num] = compute_cost(X, Y, theta)
        # 根据公式计算梯度，来更新theta的值
        hyp = np.dot(X, np.transpose(theta))
        theta = theta - alpha * np.dot(np.transpose(hyp - Y), X) / m
    return theta, J_history

# ======== 1.读取数据并标准化数据的特征 ========
data = np.loadtxt(r'ex1data2.txt',delimiter =',')
Xdata = data[:,0:2]
Ydata = data[:,2]
# 对输入数据特征进行标准化
X,mu,sigma = feature_normalize(Xdata)
# print('Mu is:',mu)
# print('Sigma is:',sigma)
X = np.c_[np.ones(X.shape[0]),X]
Y = Ydata

# ======== 2.使用梯度下降法求解 ========
theta_init = np.zeros(X.shape[1])
alpha = 0.05
num_iters = 1400

theta,J_history = gradient_descent(X,Y,theta_init,alpha,num_iters)
plt.figure()
plt.plot(np.arange(J_history.size),J_history)
plt.xlabel('Number of iterations')
plt.ylabel('Cost J')
#plt.axis([0,num_iters,0,100])
plt.show()
# theta是数组格式，格式化输出时，不能像下面那样{:0.3f}
print('Theta computed from gradient descent : \n{}'.format(theta))

# ======== 3.预测 ========
Xtest = np.array([1,1650,3])
price = np.dot(Xtest,np.transpose(theta))
print('Predicted price of a 1650 sq-ft, 3 br house (using normal equations) : {:0.3f}'.format(price))