Lesson 8.1&8.2 单层回归神经网络&torch.nn.Linear实现单层回归神经网络的正向传播

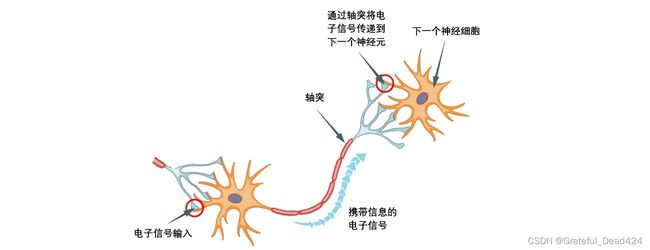​​​​​​​​在之前的介绍中，我们已经了解了神经网络是模仿人类大脑结构所构建的算法，在人脑里，我们有轴突连接神经元，在算法中，我们用圆表示神经元，用线表示神经元之间的连接，数据从神经网络的左侧输入，让神经元处理之后，从右侧输出结果。

上图是一个最简单的神经元的结构。从这里开始，我们正式开始认识神经网络。

一、单层回归网络：线性回归

1 单层回归网络的理论基础

许多人都以为神经网络是一个非常复杂的算法，其实它的基本原理其实并不难理解。还记得我们在讲解GPU那一节曾提到过的，深度学习中的计算是“简单大量”，而不是”复杂的单一问题“吗？神经网络的原理很多时候都比经典机器学习算法简单。了解神经网络，可以从线性回归算法开始。在之前的课程中，我们讲解过PyTorch基本数据结构Tensor和基本库Autograd，在给autograd举例时，我们对线性回归其实已经有简单的说明，在这里，给大家复习一下，并且明确一些数学符号。

线性回归算法是机器学习中最简单的回归类算法，多元线性回归指的就是一个样本对应多个特征的线性回归问题。假设我们的数据现在就是二维表，对于一个有个特征的样本而言，它的预测结果可以写作一个几乎人人熟悉的方程：
$${\hat{z}}_i=b+w_1{x}_{i1}+w_2{x}_{i2}+\dots +w_n{x}_{in}$$
$w$和$b$被统称为模型的权重，其中b被称为截距(intercept)，也叫做偏差(bias)，$w_1$~$w_n$被称为回归系数(regression coefficient)，也叫作权重(weights)，$w_{i1}$~$w_{in}$是样本 上的不同特征。这个表达式，其实就和我们小学时就无比熟悉的$y=ax+b$是同样的性质。其中$y$被我们称为因变量，在线性回归中表示为$z$，在机器学习中也就表现为我们的标签。如果写作$z$ ，则代表真实标签。如果写作$\hat{z}$（读作z帽或者zhat），则代表预测出的标签。模型得出的结果，一定是预测的标签。

如果考虑我们有m个样本，则回归结果可以被写作：

$$\hat{\mathbf{z}}=b+w_1{\mathbf{x}}_1+w_2{\mathbf{x}}_2+\dots +w_n{\mathbf{x}}_n$$

其中$\hat{z}$是包含了m个全部的样本的预测结果的列向量。注意，我们通常使用粗体的小写字母来表示列向量，粗体的大写字母表示矩阵或者行列式。并且在机器学习中，我们默认所有的一维向量都是列向量。我们可以使用矩阵来表示上面多个样本的回归结果的方程，其中$w$可以被看做是一个结构为(n+1,1)的列矩阵（这里的n加上的1是我们的截距b）， 是一个结构为(m,n+1)的特征矩阵（这里的n加上的1是为了与截距b相乘而留下的一列1，这列1有时也被称作$x_0$），则有：
$$\begin{array}{rl}\left[\begin{array}{c}{\hat{z}}_1\\ {\hat{z}}_2\\ {\hat{z}}_3\\ \dots \\ {\hat{z}}_m\end{array}\right]& =\left[\begin{array}{cccccc}1& x_{11}& x_{12}& x_{13}& \dots & x_{1n}\\ 1& x_{21}& x_{22}& x_{23}& \dots & x_{2n}\\ 1& x_{31}& x_{32}& x_{33}& \dots & x_{3n}\\ & & \dots & & & \\ 1& x_{m1}& x_{m2}& x_{m3}& \dots & x_{mn}\end{array}\right]\ast \left[\begin{array}{c}b\\ w_1\\ w_2\\ \dots \\ w_n\end{array}\right]\\ & \hat{\mathbf{z}}=\mathbf{X}\mathbf{w}\end{array}$$
如果在我们的方程里没有常量b，我们则可以不写$X$中的第一列以及$w$中的第一行。

线性回归的任务，就是构造一个预测函数来映射输入的特征矩阵$X$和标签值$y$的线性关系。这个预测函数的图像是一条直线，所以线性回归的求解就是对直线的拟合过程。预测函数的符号在不同的教材上写法不同，可能写作$f(x)$,$y_w(x)$或者$h(x)$等等形式，但无论如何，这个预测函数的本质就是我们需要构建的模型，而构造预测函数的核心就是找出模型的权重向量$w$，也就是求解线性方程组的参数（相当于求解$y=ax+b$里的$a$与$b$）。

现在假设，我们的数据只有2个特征，则线性回归方程可以写作如下结构：
$$\hat{z}=b+x_1{w}_1+x_2{w}_2$$

此时，我们只要对模型输入特征$x_1$,$x_2$的取值，就可以得出对应的预测值$\hat{z}$。神经网络的预测过程是从神经元左侧输入特征，让神经元处理数据，并从右侧输出预测结果。这个过程和我们刚才说到的线性回归输出预测值的过程是一致的。如果我们使用一个神经网络来表达线性回归上的过程，则可以有：
​
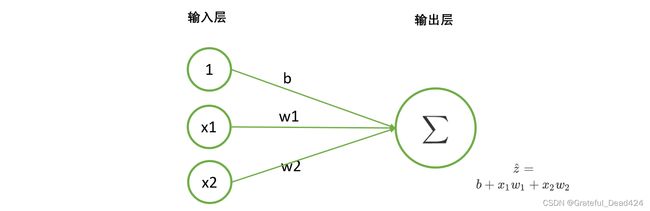
这就是一个最简单的单层回归神经网络的表示图。

在神经网络中，竖着排列在一起的一组神经元叫做“一层网络”，所以线性回归的网络直观看起来有两层，两层神经网络通过写有参数的线条相连。我们从左侧输入常数1和特征取值$x_1$,$x_2$，再让它们与相对应的参数相乘，就可以得到$b$，$w_1{x}_1$，$w_2{x}_2$三个结果。这三个结果通过连接到下一层神经元的直线，被输入下一层神经元。我们在第二层的神经元中将三个乘积进行加和（使用符号$\sum$表示），就可以得到加和结果$\hat{z}$，即$b+w_1{x}_1+w_2{x}_2$，这个值正是我们的预测值。可见，线性回归方程与上面的神经网络图达到的效果是一模一样的。

在上述过程中，左侧的是神经网络的输入层（input layer）。输入层由众多承载数据用的神经元组成，数据从这里输入，并流入处理数据的神经元中。在所有神经网络中，输入层永远只有一层，且每个神经元上只能承载一个特征(一个$x$)或一个常量（通常都是1）。现在的二元线性回归只有两个特征，所以输入层上只需要三个神经元，包括两个特征和一个常量，其中这里的常量仅仅是被用来乘以偏差用的。对于没有偏差的线性回归来说，我们可以不设置常量1。

右侧的是输出层（output layer）。输出层由大于等于一个神经元组成，我们总是从这一层来获取预测结果。输出层的每个神经元上都承载着单个或多个功能，可以处理被输入神经元的数据。在线性回归中，这个功能就是“加和”，当我们把加和替换成其他的功能，就能够形成各种不同的神经网络。

在神经元之间相互连接的线表示了数据流动的方向，就像人脑神经细胞之间相互联系的“轴突”。在人脑神经细胞中，轴突控制电子信号流过的强度，在人工神经网络中，神经元之间的连接线上的权重也代表了“信息可通过的强度。最简单的例子是，当$w_1$为0.5时，在特征$x_1$上的信息就只有0.5倍能够传递到下 一层神经元中，因为被输入到下层神经元中去进行计算的实际值是0.5$x_1$。相对的，如果$x_1$是2.5，则会传递2.5倍的$x_1$上的信息。因此，有的深度学习课程会将权重$w$比喻成是电路中的”电压“，电压越大，则电信号越强烈，电压越小，信号也越弱，这都是在描述权重$w$会如何影响传入下一层神经元的信息/数据量的大小。

到此，我们已经了解了线性回归的网络是怎么一回事，它是最简单的回归神经网络，同时也是最简单的神经网络。类似于线性回归这样的神经网络，被称为单层神经网络。

2 tensor实现单层神经网络的正向传播

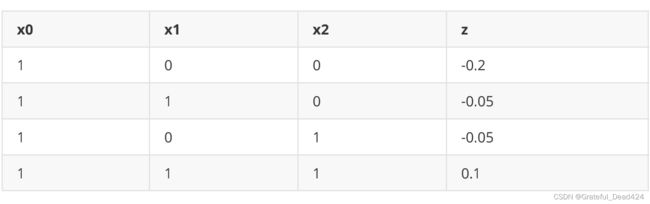
让我们使用一组非常简单（简直是简单过头了）的代码来实现一下回归神经网络求解的过程，在神经网络中，这个过程是从左向右进行的，被称为神经网络的正向传播（forwardspread）（当然，这是正向传播中非常简单的一种情况）。来看下面这组数据：

我们将构造能够拟合出以上数据的单层回归神经网络：

import torch
X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]], dtype = torch.float32) 
z = torch.tensor([-0.2, -0.05, -0.05, 0.1])
w = torch.tensor([-0.2,0.15,0.15])

def LinearR(X,w):
    zhat = torch.mv(X,w)
    return zhat
zhat = LinearR(X,w)
zhat
#tensor([-0.2000, -0.0500, -0.0500,  0.1000])

3 tensor计算中的新手陷阱

接下来，我们对这段代码进行详细的说明：

#导入库
import torch
#首先生成特征张量
X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]])
#我们输入的是整数，默认生成的是int64的类型
X.dtype
#torch.int64
#查看一下特征张量是什么样子
X
#tensor([[1, 0, 0],
#        [1, 1, 0],
#        [1, 0, 1],
#        [1, 1, 1]])
X.shape
#torch.Size([4, 3])
#生成标签

z = torch.tensor([-0.2, -0.05, -0.05, 0.1])
#标签我们输入的是浮点数，默认生成的则是float32的类型
z.dtype
#torch.float32
#查看标签
z
#tensor([-0.2000, -0.0500, -0.0500,  0.1000])

#定义常量b和权重w
#注意，常量b所在的位置必须与特征张量X中全为1的那一列所在的位置相对应，在这里，-0.2是b, 0.15是两个w
w = torch.tensor([-0.2,0.15,0.15])
w.shape
#torch.Size([3])

• tensor计算中的第一大坑： PyTorch的静态性

#定义线性回归计算的函数
def LinearR(X,w):
    zhat = torch.mv(X,w)
    #矩阵与向量相乘，使用函数torch.mv。注意，矩阵与向量相乘时，向量必须写作第二个参数。   
    #float32与int64相乘会出现什么问题？看似是个问题，其实这是PyTorch计算快速的秘诀之一。
    return zhat

#因此之后需要修改成：
def LinearR(X,w):
    zhat = torch.mv(X.float(),w)
    return zhat

#你还可以使用大写的Tensor来解决这个问题，但这个方法并不推荐：
X_ = torch.Tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]])
X_.dtype
#torch.float32

#或者，你可以直接养成好习惯：
X = torch.tensor([[1,0,0],[1,1,0],[1,0,1],[1,1,1]], dtype = torch.float32)

'''
PyTorch中的许多函数都不接受浮点型的分类标签，但也有许多函数要求真实标签的类型必须与预测值的类型一致，因此标签的类型定义总是一个容易踩坑的地方。通常来说，我们还是会将标签定义为float32，如果在函数运行时报错，要求整形，我们再使用.long()方法将其转换为整型。

另一个非常容易踩坑的地方是， PyTorch中许多函数不接受一维张量
但同时也有许多函数不接受二维标签(￣_￣|||)
因此我们在生成标签时，可以默认生成二维标签，若函数报错说不能接受二维标签，我们再使用view()函数将其调整为一维。
'''

可以看到，只要能够给到适合的w和b，回归神经网络其实非常容易实现。在这里，我们需要提出PyTorch中另一个比较严肃的问题。
最安全的办法定义的时候都把类型写上float32，标签来说定义成二维的。

• tensor计算中的第二大坑：精度问题
  来看这段代码。

zhat == z
#tensor([ True, False, False, False])
zhat.dtype
#torch.float32
z.dtype
#torch.float32
#为什么会出现这种现象呢？还记得如何衡量线性回归的结果优劣吗？

在多元线性回归中，我们的使用SSE（误差平方和，有时候也叫做RSS残差平方和）来衡量回归的结果优劣：
$$SSE=\sum _{i=1}^m{\left(z_i-{\hat{z}}_i\right)}^2$$
如果预测值${\hat{z}}_i$与真实值$z_i$完全相等，那SSE的结果应该为0。在这里，SSE虽然非常接近0，但的确是不为0的。

SSE = sum((zhat - z)**2)
SSE
#tensor(8.3267e-17)

#设置显示精度，再来看yhat与y_reg
torch.set_printoptions(precision=30) #看小数点后30位的情况
zhat
#tensor([-0.200000002980232238769531250000, -0.049999997019767761230468750000,
#        -0.049999997019767761230468750000,  0.100000008940696716308593750000])
z
#tensor([-0.200000002980232238769531250000, -0.050000000745058059692382812500,
#        -0.050000000745058059692382812500,  0.100000001490116119384765625000])
#精度问题在tensor维度很高，数字很大时，也会变得更大
#float32由于只保留32位，所以精确性会有一些问题
#torch.mv这个函数在进行计算的时候，内部计算时会出现一些很微小的进度问题

preds = torch.ones(300, 68, 64, 64) * 0.1
'''preds.shape #运行查看preds的结构'''
preds.sum() * 10
#tensor(83558328.)
preds = torch.ones(300, 68, 64, 64)
preds.sum()
#tensor(83558400.)
#怎么解决这个问题呢？

#与Python中存在Decimal库不同，PyTorch设置了64位浮点数来尽量减轻精度问题
preds = torch.ones(300, 68, 64, 64, dtype=torch.float64) * 0.1
preds.sum() * 10
#tensor(83558400.000000059604644775390625000000, dtype=torch.float64)

#但即便如此，我们也不能完全消除掉精度问题所带来的区别,如果你希望能够无视掉非常小的区别，而让两个张量的比较结果展示为True，你可以使用下面的代码:
torch.allclose(zhat,z)
#True

4 torch.nn.Linear实现单层回归神经网络的正向传播

在PyTorch中，我们使用类torch.nn.Linear类来实现单层回归神经网络，不过需要注意的是， 它可不是代表单层回归神经网络这个算法。还记得之前我们的架构图吗？

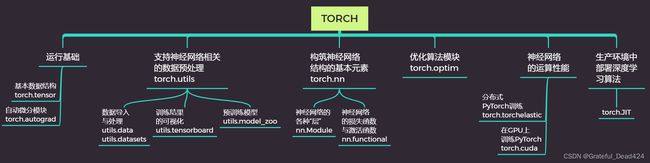
从这张架构图中我们可以看到，torch.nn是包含了构筑神经网络结构基本元素的包，在这个包中，你可以找到任意的神经网络层。这些神经网络层都是nn.Module这个大类的子类。我们的torch.nn.Linear就是神经网络中的”线性层“，它可以实现形如$\hat{\mathbf{z}}=\mathbf{X}\mathbf{w}$的加和功能。在我们的单层回归神经网络结构图中，torch.nn.Linear类表示了我们的输出层。现在我们就来看看它是如何使用的。

回顾一下我们的数据：
接下来，我们使用nn.Linear来实现单层回归神经网络：

import torch
'''只需要真正的特征矩阵,x0不需要'''
X = torch.tensor([[0,0],[1,0],[0,1],[1,1]], dtype = torch.float32,requires_grad=True)
output = torch.nn.Linear(2,1)
zhat = output(X)
zhat
#tensor([[ 0.0972],
#        [ 0.4869],
#        [-0.1768],
#        [ 0.2129]], grad_fn=)

怎么样，代码是不是异常简单？但在这段代码中，却有许多细节需要声明：

nn.Linear是一个类，在这里代表了输出层，所以我使用output作为变量名，output = 的这一行相当于是类的实例化过程

实例化的时候，nn.Linear需要输入两个参数，分别是（上一层的神经元个数——上一层的神经元中，给这一层传输数据的神经元的个数，这一层的神经元个数——接收传输数据的神经元的个数）。上一层是输入层，因此神经元个数由特征的个数决定（2个）。这一层是输出层，作为回归神经网络，输出层只有一个神经元。因此nn.Linear中输入的是（2，1）。

我只定义了X，没有定义w和b。所有nn.Module的子类，形如nn.XXX的层，都会在实例化的同时随机生成w和b的初始值。所以实例化之后，我们就可以调用以下属性来查看生成的和：

output.weight #查看生成的w
#Parameter containing:
#tensor([[ 0.3897, -0.2741]], requires_grad=True)
output.bias #查看生成的b
#Parameter containing:
#tensor([0.0972], requires_grad=True)

其中，w是必然会生成的，b是我们可以控制是否要生成的。在nn.Linear类中，有参数bias，默认bias = True。如果我们希望不拟合常量b，在实例化时将参数bias设置为False即可：

output = torch.nn.Linear(2,1,bias=False)
#再次调用属性weight和bias
output.weight
#Parameter containing:
#tensor([[ 0.0868, -0.3132]], requires_grad=True)
output.bias

由于w和b是随机生成的，所以同样的代码多次运行后的结果是不一致的。如果我们希望控制随机性，则可以使用torch中的random类。如下所示：

torch.random.manual_seed(888) #人为设置随机数种子
output = torch.nn.Linear(2,1)
zhat = output(X)
zhat
#tensor([[-0.5236],
#        [-1.1635],
#        [-0.2499],
#        [-0.8898]], grad_fn=)

由于不需要定义常量b，因此在特征张量中，也不需要留出与常数项相乘的x0那一列。在输入数据时，我们只输入了两个特征x1与x2

输入层只有一层，并且输入层的结构（神经元的个数）由输入的特征张量决定，因此在PyTorch中构筑神经网络时，不需要定义输入层
实例化之后，将特征张量输入到实例化后的类中，即可得出输出层的输出结果。
让我们来看看输出结果的形状：

zhat.shape
#torch.Size([4, 1])

这个形状与我们自己定义的z是一致的。但就数字大小上来说，由于我们没有自己定义w和b，所以我们无法让nn.Linear输出的zhat与我们真实的z接近——让真实值与预测值差异更小的部分，我们会在之后进行讲解。现在，让我们继续了解神经网络。在下一节中，我们会将单层回归神经网络的例子推广到分类问题上。