语音信号线性预测分析（MATLAB实战篇）

前言

在学习线性预测分析的过程中，也是发现其应用比较广泛，参数的用途很多，如果不总结一下，脑袋就瓜嗡嗡的！所以呢，我就简单总结一下线性预测分析在语音信号处理中的一些用途吧！内容肯定是不全的，我主要总结了由线性预测分析得到一些基本参数，并分析这些参数有啥实际应用，通过MTALAB编写程序来实现。

基本概念

在学习之前，我们需要弄清楚几个基本问题。什么是线性预测分析，以及为什么要进行线性预测分析？线性预测分析能有啥用？

首先，必须知道线性预测分析的一个重要概念就是，一个语音信号的当前采样值能够用其过去若干采样值的线性组合来逼近，使其具备和原语音信号同样的“特征”。这里的“特征”强调两者等同，即各方面完全一致。而线性预测分析就是在这个逼近过程中，依据实际采样值与预测采样值两者误差值最小原则，确定一个预测模型的过程。也就是决定唯一的一组预测系数（LPC）的过程。然后依据这组预测系数可以还原一个完整的语音信号。反过来说就是，由实际语音信号决定一组预测器系数（LPC），使得预测误差在某个准则（最小均方误差准则）下最小的这一过程，就叫做线性预测分析。简单概括，线性预测分析就是由实际语音信号求LPC的过程。

重要性：线性预测分析之所以如此重要，主要还是求解得到的线性预测系数LPC太重要。LPC是语音信号处理中的重要重要参数，用途十分广泛。可以用来估计很多语音参数，如基音周期、共振峰、声道面积函数，以及用于语音编码、语音合成和语音识别等领域。更具体而言，LPC的优势在于能够用少量的参数就可以有效而正确的表现出原语音信号的时域和频域特性；除此之外，LPC还能够提供一个很好的声道模型，这对于语音识别和语音合成非常重要！！！下面我将主要讲述一下线性预测系数LPC及其衍生参数的求解和用途吧。附有代码实现！

基本参数的求解及其用途

1、线性预测系数（LPC）

根据上文的分析可知，线性预测分析的过程就是求解一组线性预测系数LPC。因此LPC是线性预测分析的主要参数，其他参数都是由LPC推演出来的。严格上来讲，一个完整的线性预测分析过程是需要求解LPC和其增益。其基本原理如下图所示，

线性预测分析的过程就是将被分析信号用一个模型来表示，即将预测信号看成某个系统或模型H(z)的输出。其中，u(n)表示模型的输入。对于发浊音信号（汉语韵母），模型的输入u(n)可采用周期性单位冲击序列；对于发清音信号（汉语声母），模型的输入u(n)可采用随机白噪声序列。而对于模型的传输函数H(z)目前更多是采用自回归AR模型，其传递函数H(z)和x(n)的线性常系数差分方程（时域表达）的表达式如下：

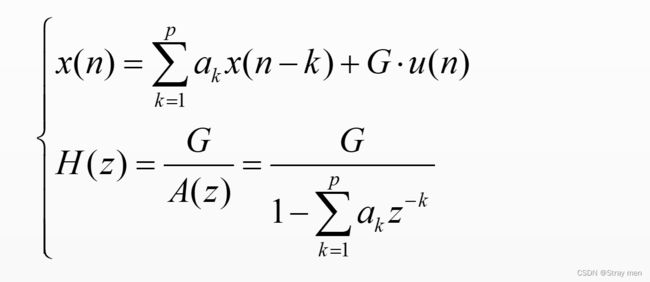
AR模型的含义是：该模型当前的输出是由当前的输入u(n)和过去p个输出x(n-k)的加权之和。线性预测分析就是求解传递函数H(z)的过程，即求出一组线性预测系数a(k)和增益G。那么该如何求解LPC和增益G？

先定义线性预测器的差分方程和传递函数P(z)如下。因为线性预测的核心要义就是，当前的输出x(n)是若干个过去输出的线性组合。

则线性预测误差序列e(n)为实测语音序列x(n)与预测序列的差，其差分方程和传递函数A(z)的表达式如下：

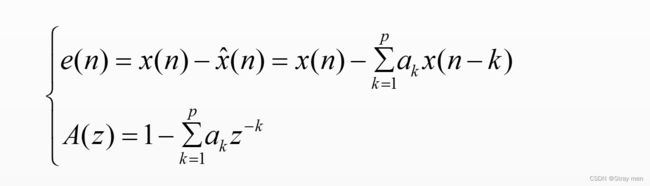
既有，

观察（4）和开头那个式子可知，如果语音信号准确服从AR模型，且有e(n)=Gu(n)，则线性预测误差序列e(n)的传递函数A(z)与预测系统模型H(z)互为倒数，即预测误差滤波器A(z)是系统模型H(z)的逆滤波器。满足关系如下：

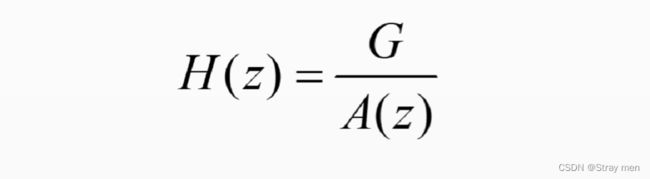
因此，要求解H(z)可以直接由预测误差滤波器的传递函数A(z)来求解。而预测误差序列是实测信号与预测信号的差值，由于误差值始终存在，要求出LPC则必须依赖某个准则，这个准则通常采用最小均方误差准则。故预测二次方误差E可表示为，

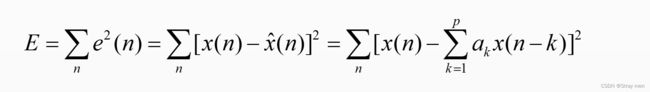
而要求解LPC应该使得预测二次方误差对每一个预测系数a(k)的偏导数为0，由此可得方程，

求解这个方程就可以得到对应的LPC。下面给出几种实际求解LPC的方法。由于原理部分太繁琐了，下面先介绍流程，然后直接给出MATLAB求解函数，我相信这部分才是你们最关心的。
（1）自相关法
自相关法是在整个时间段内使得误差值最小，计算LPC的流程如下图所示。

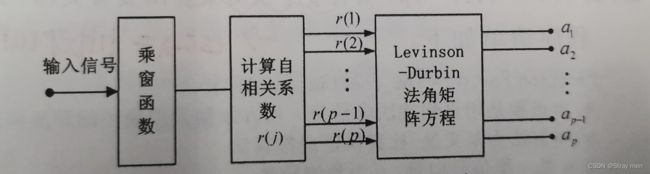
代码实现：
MATLAB中自带了几个利用自相关法计算LPC的函数，下面分别说明。
1、函数lpc_coefficientm
该函数是利用莱文逊-杜宾自相关法来计算LPC，由预测误差滤波器的传递函数A(z)计算得到，调用格式如下：

[ar,G]=lpc_coefficientm(s1,p);%s1为一帧语音信号，p为阶数；
%输出ar为预测系数LPC（p个），G为增益。

2、函数lpc和lpcauto
这两个函数放在一起是因为得到的结果一样。但是要注意一点，此处计算LPC是由预测误差滤波器传递函数的另一形式得到，其传递函数A’(z)的表达式如下：

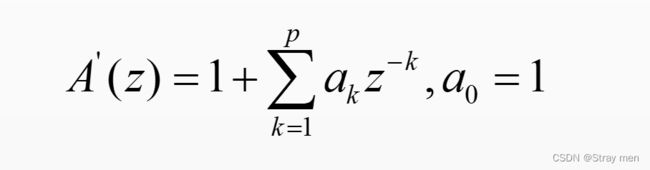
因此，经过计算得到的LPC将有p+1个，且第一个a0永远为1。更重要的是，计算得到的LPC与实际值相反，因为实际误差滤波器的传递函数A(z)是减号关系；而这里是加号。其调用格式如下：

[ar,e]=lpc(s1,p);%s1为一帧语音信号，ar为LPC个数（p+1），且第一个系数a0为1
[ar,e,k]=lpcauto(s1,p);%e为计算得到的最小均方误差，开根计算得到增益G，k为反射系数。

（2）协方差法
协方差法计算LPC与自相关法不同之处在于，协方差法不规定计算信号的时间长度，而是把样点数固定下来。其计算流程图如下：

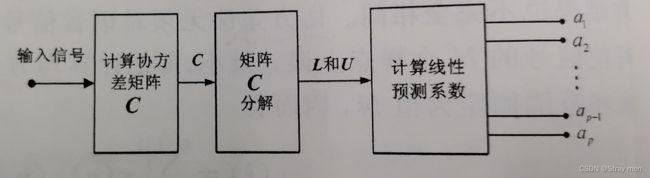
函数调用：

[ar,e]=arcov(s1,p);%与函数lpc一样，得到p+1个结果，且与实际LPC互为相反数

（3）格型法
格型法计算LPC的原理是将线性预测误差滤波器的输出分解成两部分：第一部分为前i-1阶的输出，定义为前向预测误差，该部分是通常意义上的线性预测误差，是由过去的若干样本值预测得到的误差；第二部分为与第i-1阶有关的输出信号经过单位延时和k加权后的输出，定义为后向预测误差。这部分误差可以看做是用在时间上有延迟的样本值x(n-i+1),…,x(n)来预测x(n-i)时得到的误差。关系式如下：

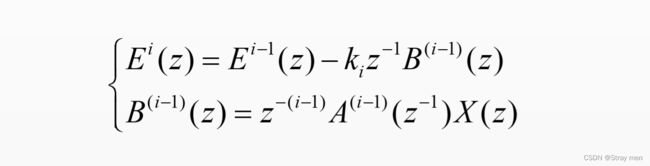
格型法的求解方法很多，有前向格型、后向格型、几何平均格型以及伯格法等。其中前向格型、后向格型计算得到的LPC稳定性得不到保证，因此常用后两种方法。这里给出利用几何平均格型法计算LPC的函数。调用格式：

[e,ar,G,k]=latticem(x,L,p);%L为做格型法处理的长度，一般和帧长相等；p为LPC阶数
%注意：此时输入一帧语音信号x的长度应该大于或者等于L+p的长度；
%输出参数ar为p*p矩阵，取第p次的预测系数（p个）。

利用上述几种方法调用MATLAB函数计算LPC的结果如下：

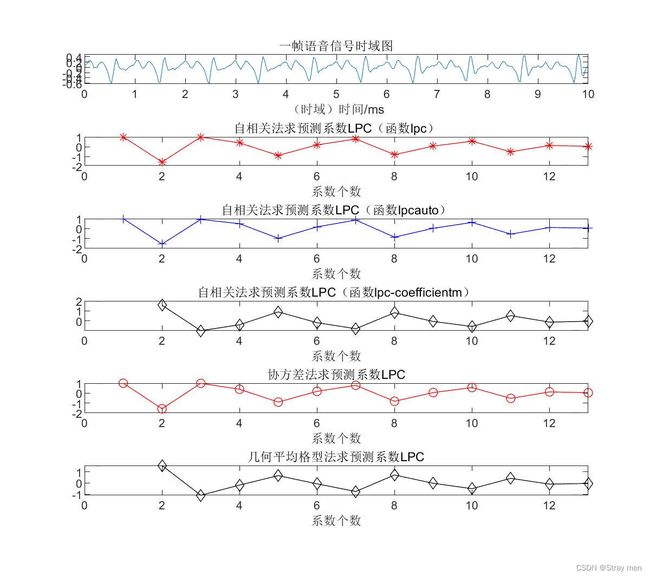
结论：
函数lpc、lpcauto和arcov计算得到的LPC阶数为p+1且与实际值相反。而函数latticem和lpc_coefficientm计算得到的LPC阶数为p个，且为正确数值。在调用函数的时候务必看清楚使用条件。
接下来使用线性预测系数LPC还原语音信号。代码如下：

% %——————————计算LPC并还原语音信号
p=8;%LPC阶数（8~12）
[ar,err]=lpc(s11,p);%计算LPC
y1=filter([0 -ar(2:end)],1,s11);%得到预测信号
er=s11-y1;%误差信号

注意：此时调用的是lpc函数计算LPC，得到的LPC与实际值相反（取负号），而且多了一个a0=1，因此从第二个系数算起。
预测结果：

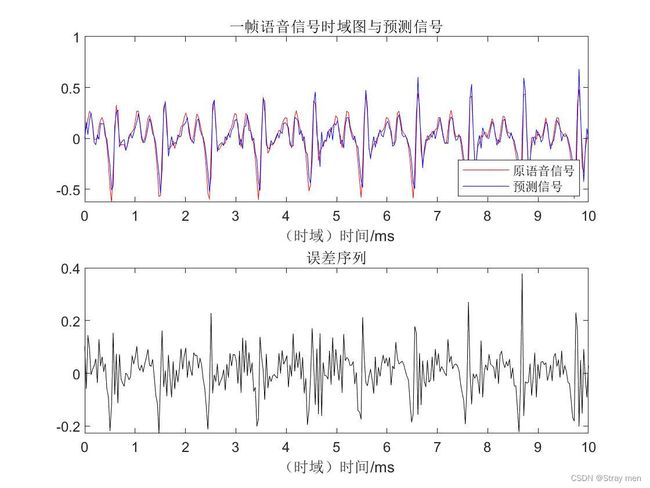
2、线性预测系数LPC的频谱

根据上文的分析可知，线性预测能够提供很好的声道模型H(z)，这个声道模型就包含了声道信息，即共振峰。因此线性预测系数LPC的频谱就能反映出共振峰，而共振峰是原信号频谱的包络线。两者的关系是，原语音信号频谱包络的极大值就是共振峰。编写程序查看图形，代码如下：

i=30;
s11=y(:,i);%取第30帧信号（有话帧）
s1=s11.*hamming(wlen);%加窗平滑
np=wlen/2;
f_s1=fft(s1);%幅值谱
f_s1=f_s1(1:(np+1));%取一半频率
f_s11=20*log10(abs(f_s1));%dB

% %——————————计算LPC的频谱
p=8;%LPC阶数（8~12）
[ar,err]=lpc(s1,p);%计算LPC
f_ar=lpcar2ff(ar,np);%计算LPC幅值谱
f_ar1=20*log10(abs(f_ar));%dB

f_ar2=lpcar2pf(ar,np);%计算LPC功率谱
f_ar22=10*log10(f_ar2);%dB
[Loc,Val]=findpeaks(f_ar2);%寻找峰值
freq=Fs/wlen*(1:(np+1));%频率刻度
F_q=freq(Loc);%找出共振频率
fprintf('共振频率F=%5.2fHZ \n',F_q);

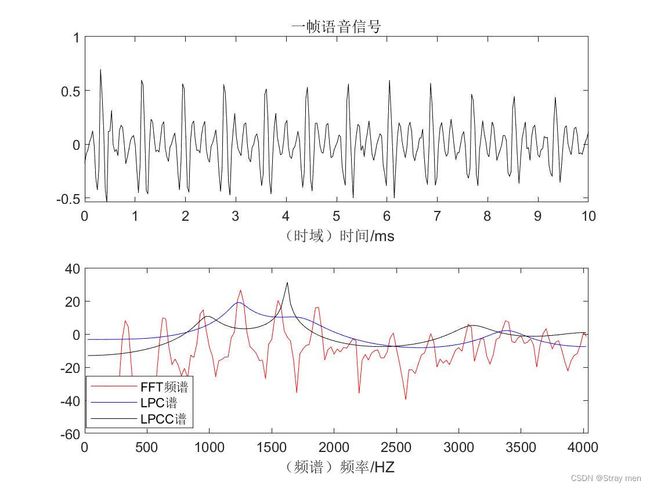
结果：
计算所得共三个共振峰，频率分布为F=1225.00HZ ，F=1650.00HZ 和F=3375.00HZ 。

结论：此一帧语音信号共有三个共振峰，对应的共振频率计算如上**。注意**：对共振峰参数的估计还需要求其带宽。一般计算**-3dB带宽**，可以用LPC的功率谱来计算。因为功率谱是频谱的平方，其结果都大于零。如果用幅值谱的话，不好计算峰值下降的0.707倍。而且对于功率谱而言，其-3dB带宽就是半功率点带宽，即幅值下降一半的位置。在实际计算时十分的便利。有兴趣的可以编代码实现一下。

3、线性预测系数的倒谱LPCC

这一部分的内容可以参照我上一篇博文，对语音信号中的倒谱做了一个相对全面的总结，还编写了代码实现。博文：‘连续语音信号的短时倒谱分析及其参数用途’
思考：这边提出一个问题，既然LPC的倒谱LPCC也反映了原语音信号的谱包络信息，那么LPCC的频谱能反映什么物理量呢？有兴趣的可以自己编写代码实现一下。下面给出结果：
LPC共振频率F=1225.00HZ 1650.00HZ 3375.00HZ，
LPCC共振频率F=975.00HZ 1625.00HZ 3125.00HZ。

4、线性预测误差e(n)及其自相关

根据上文的分析可知，如果线性预测系统服从AR模型，则线性预测误差e(n)应该逼近u(n)。而u(n)是系统的输入，不包含声道信息。因此可以用线性预测误差e(n)来提取基音周期。根据自相关函数的性质，如果系统的输入u(n)是周期信号，则其自相关信号也具有周期特性。因此也可以用其自相关来估计基音周期。其结果如下图所示。

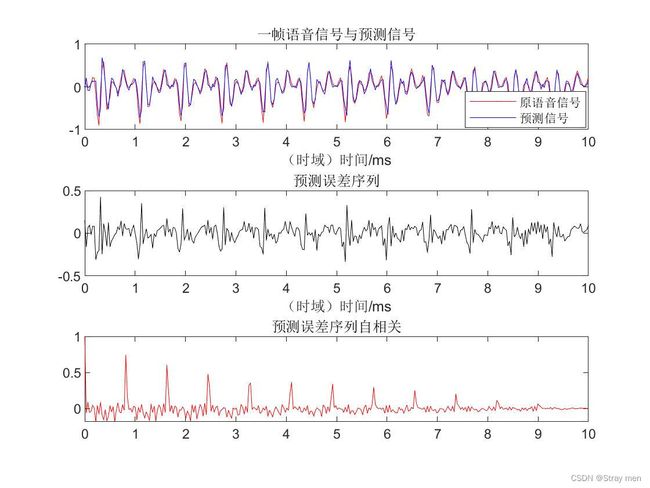
结论：从上图可知，预测误差序列和预测误差自相关序列都具有周期特性，因此可以用来提取基音周期。预测误差自相关序列峰值越来越小是因为计算自相关函数的过程中累加项越来越少，因此峰值逐渐减低（能量小了）。

在实际提取基音周期的过程中，为了进一步降低声道响应的影响，可以在计算误差序列e(n)或者自相关之后，用其倒谱或者让其通过带通滤波（60~500HZ）来估计基音周期，这样对基音周期的估计结果更加准确。关于用预测误差序列e(n)的倒谱来估计基音周期的程序可以参考另一篇博文——‘连续语音信号的短时倒谱分析及其参数用途’，这里介绍利用预测误差序列的自相关来估计基音周期。代码如下：

% %—————由预测误差序列的自相关估计基音周期————% %
p=8;%LPC阶数（8~12）
[ar,err]=lpc(s11,p);%计算LPC
y1=filter([0 -ar(2:end)],1,s11);%得到预测信号
er=s11-y1;%误差信号

er2=xcorr(er,'coeff');%计算归一化自相关
er2=er2(wlen:end);%取延迟量为正值的部分

lmin=fix(Fs/500); % 基音周期的最小值
lmax=fix(Fs/60);  % 基音周期的最大值
q1=zeros(1,320);
q=er2(lmin:lmax)';
q1(lmin:lmax)=q;%长度补齐
[r,Lc]=max(er2(lmin:lmax));%找最大值
T0=(Lc+lmin-1)/Fs;%基音周期
F0=1/T0;
fprintf('基音周期T0=%5.4f ms\n',T0*1e3);
fprintf('基音频率F0=%5.4f HZ\n',F0);

结果：
基音周期T0=3.3750 ms，基音频率F0=296.2963 HZ。

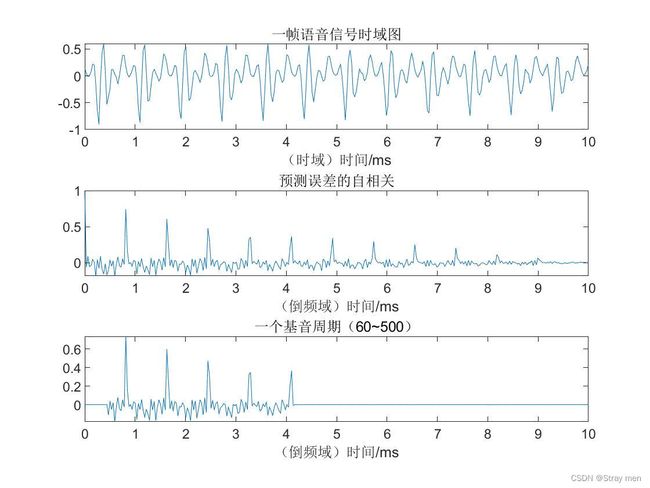
此时，仅仅取前1个基音周期，因此前一个基音周期的能量比较大。基音周期的估计数值如上所示。该结果和利用预测误差的倒谱估计基音周期数值近似。

5、预测误差滤波器A(z)多项式的根

预测误差滤波器A(z)多项式的根反映了共振峰的信息，每一对根与信号谱中的一个共振峰对应。一般由LPC计算得到的是共轭对称复根。当LPC的阶数p为偶数时，得到p/2对复根。MTALAB自带函数为，

zz=lpcar2zz(ar);%zz为复根，包含实数根和复数根。
%或者用求根函数
zz1=roots(ar);

由于预测误差滤波器A(z)多项式的根反映了共振峰信息，因此可以用其来估算共振峰。计算公式如下：

但是，在计算共振峰需要注意的一点就是，计算得到的峰值不全是共振频率，需要加上限定条件。即共振频率只有在150~fs/2范围内的才是，而且其带宽要小于700HZ。代码实现如下：

% %—————由预测误差序列的自相关估计基音周期————% %
p=8;%LPC阶数（8~12）
[ar,err]=lpc(s11,p);%计算LPC
% zz=lpcar2zz(ar)';%计算复根

zz1=roots(ar);%计算复根
n_frmnt=4;% 一帧最多取四个共振峰
const=Fs/(2*pi);  %计算常数
k=1;  % 初始化
yf = [];
bandw=[];
for i=1:length(ar)-1                     
    re=real(zz1(i));  % 取根之实部
    im=imag(zz1(i));   % 取根之虚部
    formn=const*atan2(im,re);  % 计算共振峰频率
    bw=-2*const*log(abs(zz1(i)));  % 计算带宽
    
    if formn>150 && bw <700 && formn<Fs/2     % 满足条件方能成共振峰和带宽
        yf(k)=formn;
        bandw(k)=bw;
        k=k+1;
    end
end
[y, ind]=sort(yf);% 排序输出
bw=bandw(ind);
F0 = y(:); 
Bw = bw(:);% 按列输出
fprintf('共振频率F0=%5.2fHZ   %5.2fHZ    %5.2fHZ\n',F0);
fprintf('-3dB带宽Bw=HZ%5.2fHZ   %5.2fHZ    %5.2fHZ\n',Bw);

结果：
共振频率F0=1203.13HZ 1705.38HZ 3357.71HZ；
-3dB带宽Bw=130.15HZ 341.75HZ 264.75HZ。

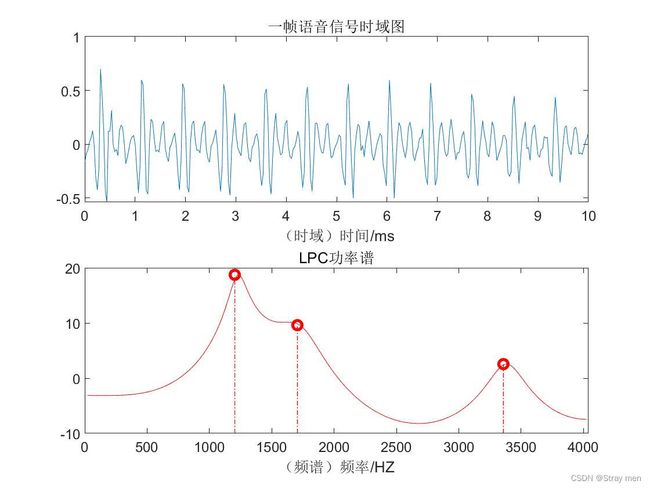
结论：此一帧语音信号的共振峰共有3个，共振频率和带宽数值如上。与利用LPC频谱计算得到的共振频率相差不大，由LPC频谱计算的数值可见参数2中所示。

6、线谱对LSP

线谱对LSP的出现是为了弥补利用线性预测系数LPC重建语音信号时会导致系统不稳定的问题。而LSP具有良好的量化特性和内插特性，其小的系数偏差带来的谱误差也是局部的，因此其稳定性能够保证。LSP在语音信号编码中应用广泛。唯一的缺点就是计算量较大。
LSP是对线性预测逆滤波器A(z)求解p+1阶对称与反对称多项式的共轭复根得到的。其对称与反对称多项式的表达式如下：

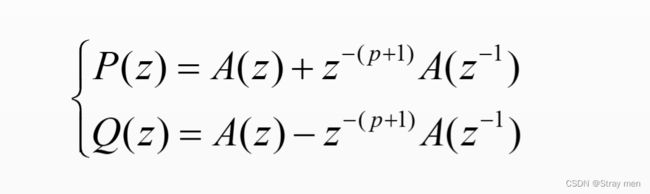
其中P(z)和Q(z)分别表示对称与反对称的实系数多项式。可以证明，当A(z)的根位于单位圆内时，P(z)和Q(z)的根都位于单位圆上，且交替出现。若假定LPC的阶数p为偶数，则此时P(z)和Q(z)各有p/2个共轭复根位于单位圆上。LSP共轭复根对应的共振峰频率称为线谱频率（LSF），即求解使得P(z)和Q(z)等于0时的频率为LSF。
LSP与LPC之间的转化：
MATLAB中有直接实现转化的函数。
（1）由LPC求LSP

lsf=ar2lsf(ar);%ar是预测系数LPC，当预测阶数为p时，需要输入p+1个ar值；lsf是得到的线谱频率，其中奇数项为P(z)的根，偶数项为Q(z)的根（线谱频率为用fs归一化角频率）
%
ls=lpcar2ls(ar);%得到的ls为归一化的频率（HZ），其他与上同

（2）由LSP求LPC

ar=lsf2ar(lsf);%和上面的函数ar2lsf对应
%
ar=lpcls2ar(ls);%和上面的函数lpcar2ls对应

参数LSP能够反映了声道幅值谱的特点，即在共振峰处LSP分布较为密集，反之较为稀疏。其结果如下所示。

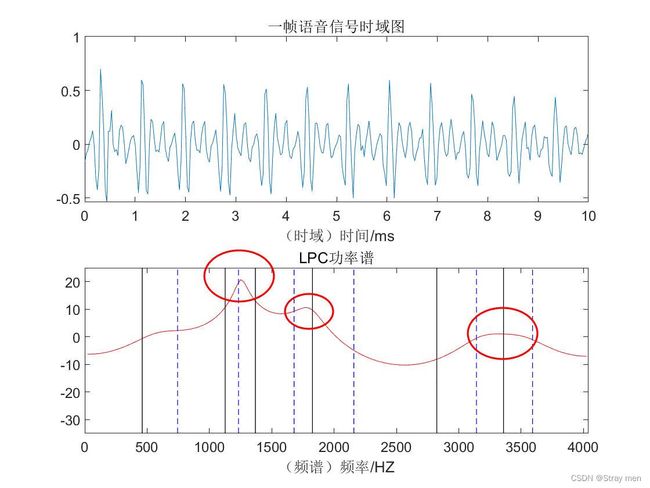
LSP在语音信号编码中的应用较为成熟，网上的资源也比较丰富，这里主要讨论利用LSP对语音信号实现变速。

LSP实现语音变速是通过对LSF内插实现。因为LSF稳定性更高。在语音变速的过程中，仅仅对语音信号在时间上拉伸，不改变信号的基频和共振峰的信息。内插仅仅是改变数量的多少。比如：原先的基音周期是10ms，现在将其在时间上拉伸为原来的两倍，即将原先10ms内的数据点扩充为2倍的样点数，只是改变数量，原先的周期10ms不变。但是要注意一点，在内插的过程中，由于采样点的位置发生了改变，原语音信号每帧对应的时刻也发生了变化，因此对语音信号变速之后不能直接将原语音信号中的信息直接搬过来用，而是需要重新合成。

这里采用的语音合成模型如下所示，即由预测系数和基音参数来合成变速后的语音信号。预测系数控制声道信息，即由LPC得到LSF，LSF的每一对根反映一个共振峰，通过对LSF内插得到变速后的LSF，在转化为LPC，得到变速后的声道参数，对应下图中的数字滤波器部分。由于拉伸后的信号每帧时刻发生变化，因此需要重新利用基音信息重新合成激励信号u(n)。变速后语音信号的基音周期可以通过对原基音周期内插得到。

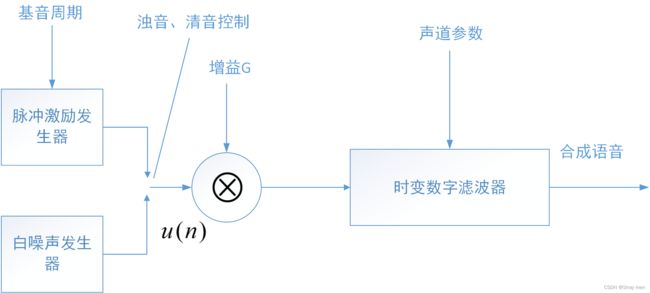
语音变速的实现步骤如下：
（1）获取原语音信号：加窗分帧
（2）计算初始参数：包括线性预测系数LPC(LSF)、增益G、基音周期T0；
（3）内插过程：包括对LSF内插、增益G内插、基音周期T0内插三部分；
（4）由LSF得到新语音信号预测系数LPC，结合新增益G1和新基音周期T1合成语音信号。
由于代码比较长，这里直接给出结果。最后我会将代码打包好上传。


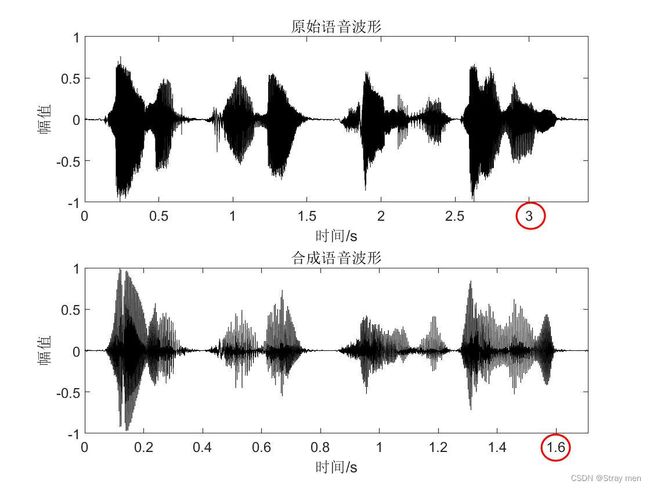
结论：这里是将语音拉伸为原来的两倍和减低为原来的一半，即分别实现减速和加速。

总结

线性预测分析在语音信号处理中的用途不局限于此，还有很多其他的用途，这里仅仅是对其进行一个简单总结。其中内容量也比较多，原理性东西阐述的不够细致。有不懂的可以参考相关书籍或者留言评论。当然，其中不免会出现问题，希望大家指出，一起交流学习。最后我把文中用到的代码都打包好上传了，有需要的可以下载。
！！！！！连续语音信号线性预测分析程序包！！！！！