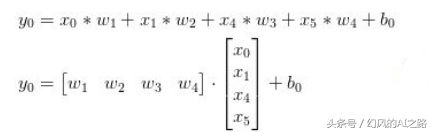孟孟单单

【积累】机器学习知识

机器学习知识

Q 问题们

1.归一化层是加在哪儿的呢，它跟数据预处理里面的归一化可不一样吧？还有dropout又是加在哪儿的，啥时候用呢？

答：归一化层一般加在全连接层FC和卷积层conv后面、激活层之前。dropout好像一般是在FC中使用，防止过拟合。

以前在神经网络训练中，只是对输入层数据进行归一化处理，却没有在中间层进行归一化处理。要知道，虽然我们对输入数据进行了归一化处理，但是输入数据经过σ ( W X + b ) 这样的矩阵乘法以及非线性运算之后，其数据分布很可能被改变，而随着深度网络的多层运算之后，数据分布的变化将越来越大。如果我们能在网络的中间也进行归一化处理，是否对网络的训练起到改进作用呢？答案是肯定的。

2.卷积核内容是怎么设置的呢？平时都是看在设置卷积核大小，没看到设置卷积核内容呢？

答：卷积核是算法自己学习得到的，也就是训练出来的。卷积核的内容代表的是权重。应该是那些什么高斯滤波之类的吧。

3.卷积核滑动窗口也有步长吗？这里的步长有什么用呢？是跟same、valid有关吗？就是做完卷积之后图像大小是否会改变。

4.不同通道的卷积核值是不一样的吗？例如这张图：

（对了，卷积核的通道数应该是与输入图像的通道数一致的）

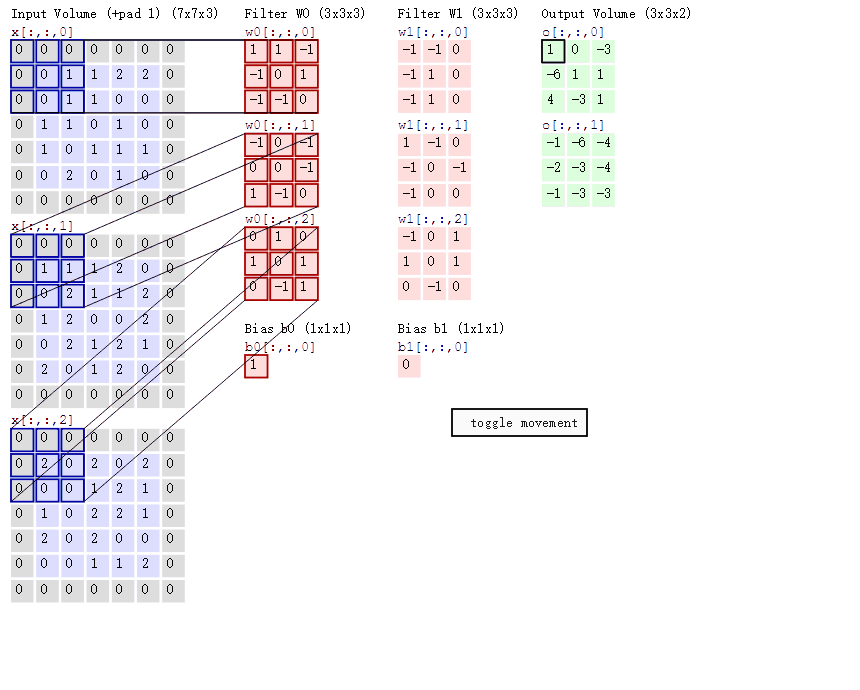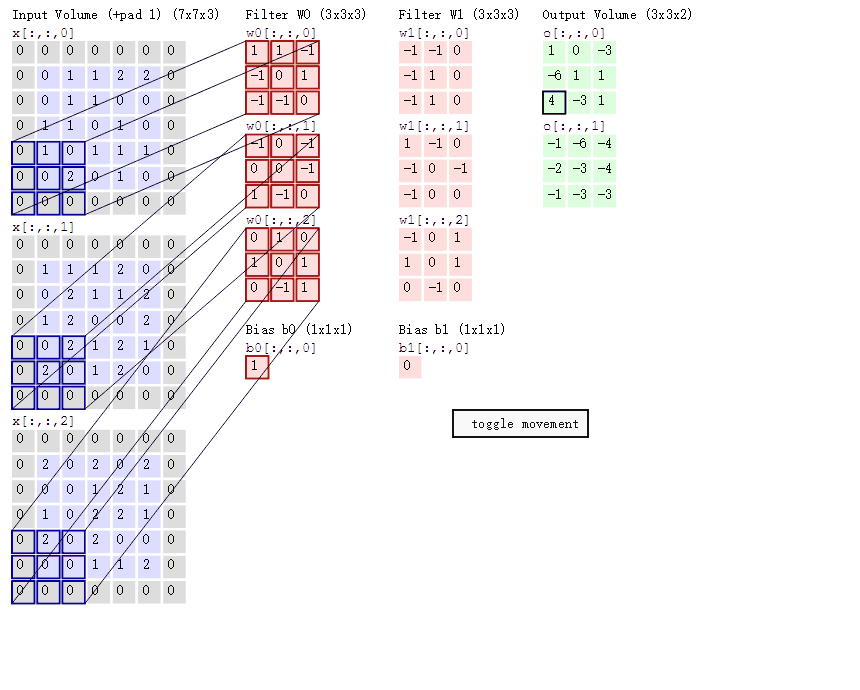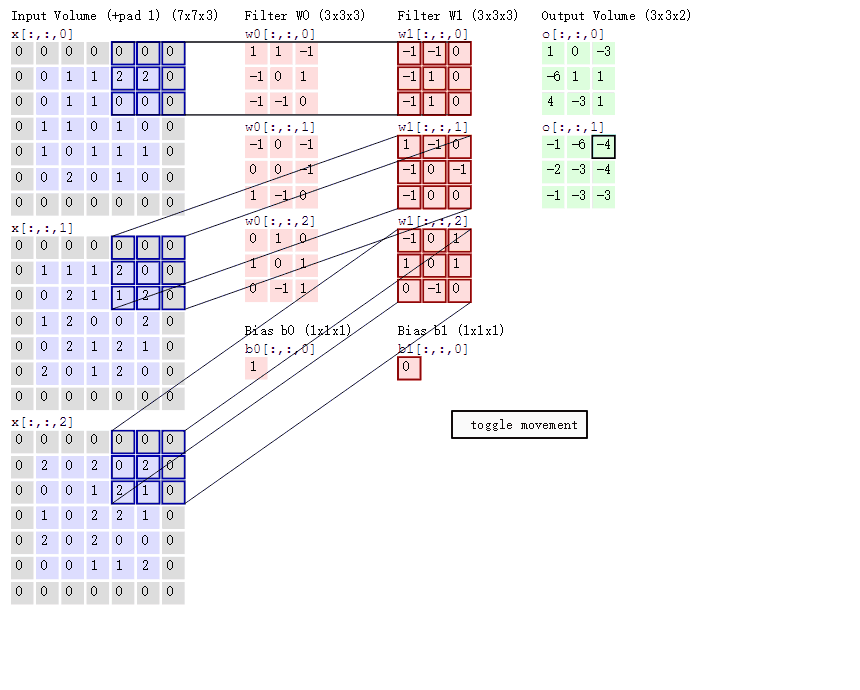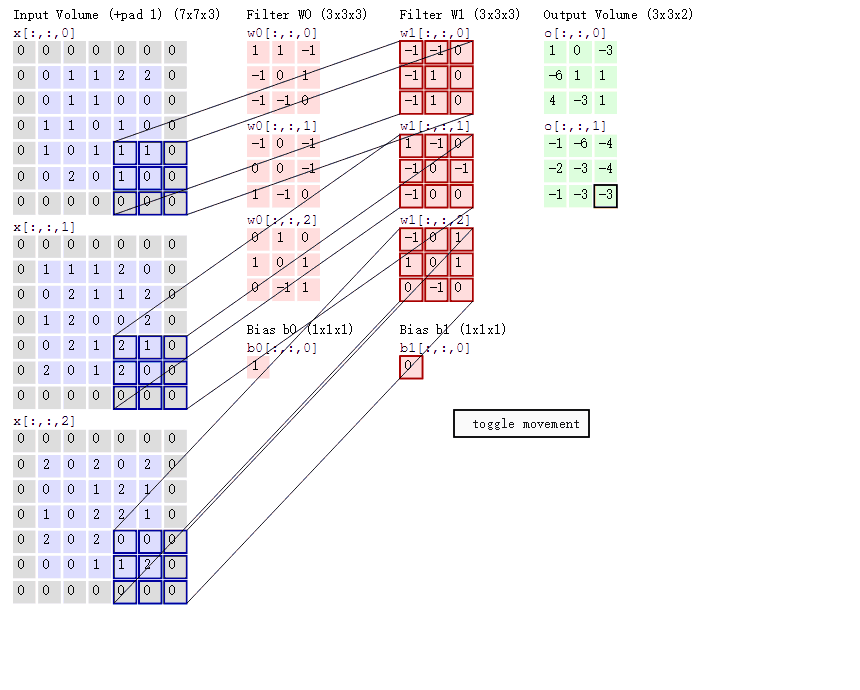
5.卷积层也有步长吗？是在代码的那个地方设置的呀？

6.1×1的卷积核有什么用？

答：大型的网络为了降低参数量都会应用上1×1卷积核。

0 一些不严谨的感觉

如果特征太多了，就是用归一化、标准化等处理。
学习sklearn这个库，里面封装了很多函数，直接调用fit进行拟合即可。
为了好拟合，一般都是寻找凸优化方案，就是使得代价函数呈现碗状，方便找到最低点。
分类问题是监督学习的最主要类型。
有些公式中取平均时，分母会多一个2，这是为了求偏导时抵消，使系数=1。
决策边界，就是模型函数绘制的曲线吧。
使用上采样、下采样的场景：（分类时）正负样本分布不均衡。
在代码中，最前面还是加上这行以免会有莫名其妙的红字显示。
```
import warnings
warnings.filterwarnings('ignore')
```
dense表示全连接层。
LRN：局部响应归一化。
变形卷积核、可分离卷积？卷积神经网络中十大拍案叫绝的操作。
在相同的网络下，pre-training + fine-tuning work的最好。论文阅读笔记：Object Detection Networks on Convolutional Feature Maps

※ 积累

※.1 数据集

工业缺陷

常用开源表面缺陷检测数据集：链接1 链接2

文物数据集

可到【全国数字博物馆集群-“博物中国”】去爬虫

※.2 数据增强方式

YOLOv5中的马赛克增强方式
高斯混合模型条件生成式对抗网络数据增强算法
利用Albumentations工具进行数据增强。Pytorch使用albumentations实现数据增强
预处理
- 对原始数据进行图像分割，然后进行图像尺寸归一化，并通过平移、翻转等数据操作扩充数据集
- 直接对原始数据集进行尺寸归一化并进行不同角度的数据增强翻转
Keras提供的图像数据增强工具Image Data Generator

※.3 Github代码

1 一些基本概念

1.0 监督们的定义

参考博客：有监督、半监督、无监督、弱监督、自监督的定义和区别

全监督、半监督、无监督学习简单比喻

有监督：用有标签的数据训练；（平时做的题目，有答案，而且参考答案全对；）
无监督：用无标签的数据训练；（平时做的题目完全没有答案；）
半监督：同时用有标签和无标签的数据进行训练。最近非常火热，此领域的发展也非常迅速，先前通常是两阶段的训练，先用（较小规模的）有标签数据训练一个Teacher模型，再用这个模型对（较大规模的）无标签数据预测伪标签，作为Student模型的训练数据；目前已经有很多直接end-to-end地训练，大大减少半监督训练的工作；（平时做的题目，半部分有答案；）
自监督：在无标注数据上训练，通过一些方法让模型学习到数据的inner representation，再接下游任务，例如加一个mlp作为分类器等。但接了下游任务之后还是需要在特定的有标签数据上finetune，只是有时候可以选择把前面的层完全固定，只finetune后面接的网络的参数。（域适应：在平时做的题目中，总结训练，将经验迁移到高考中，做出答案。）
弱监督：用包含噪声的有标签数据训练。（平时做的题目，有答案，但答案不一定全对；）

以上各个概念的分类并不是严格互斥的。

1.1 性能评价指标

1.1.0 baseline,backbone和benchmark

一般用benchmark data 做实验，测试A B C D四个模型，然后以结果最差的一个模型，假设是C，作为baseline，看看其他模型相对C提高了多少。

直接用别人的模型做baseline，然后在别人的模型上添加各种components。那这个时候可以把baseline看成benchmark。我的理解就是benchmark就是一种大家认可的标准，在不同的语境中benchmark指代可能有所区别，比如有人弄了个很不错的数据集，这个数据集对应某个task，那么这个作者一定会提出一个解决这个task的模型，然后很多人都follow这个task，自然这个数据集就是benchmark data，这个方法就是benchmark method（model）。baseline和benchmark有什么区别？

baseline（基线）：是模型能够达到的最差的效果；
benchmark：是目前的模型能做到的比较好的效果了；再往上就是state of art（SOTA）业界顶尖了。
backbone（核心、支柱）：骨干网络。在神经网络中，尤其是CV领域，一般先对图像进行特征提取（常见的有vggnet，resnet，谷歌的inception），这一部分是整个CV任务的根基，因为后续的下游任务都是基于提取出来的图像特征去做文章（比如分类，生成等等）。backbone是什么意思

1.1.1 模型评估指标AUC（area under the curve）

AUC在机器学习领域中是一种模型评估指标。根据维基百科的定义，AUC(area under the curve)是ROC曲线下的面积。

参考博文：模型评估指标AUC（area under the curve）

评价指标要好好的去设计一下，因为正负样本可能不均衡。

1.1.2 二分类问题

正样本（positive）、负样本（negative）

1.正确肯定（true positive，TP）：预测为真，实际为真

2.正确否定（true negative，TN）：预测为假，实际为假

3.错误否定（false negative，FN）：预测为假，实际为真。

4.错误肯定（false positive，FP）：预测为真，实际为假。

混淆矩阵Confusion matrix

召回率（recall），也称真阳性率（true positive rate,TPR），灵敏度，查全率。（实际正样本中被预测为正的概率，横着看）
$\operatorname{Recall}(T P R)=\frac{T P}{T P+F N}$
精确度(precision)也称精度，查准率，阳性预测值(positive predictive value, PPV)。（预测为正样本中被预测为正的概率，竖着看）
$\operatorname{Precision}(PPV)=\frac{TP}{TP+FP}$
Dice 相似系数也称 F1 分数(F1-Score)，描述的是召回率与精确度之间的关系，公式为：
$\operatorname{Dice}=\frac{2TP}{2TP+FP+FN}$
或
$\operatorname{F_1}=\frac{2×PPV×TPR}{PPV+TPR}$
F1 是一个特殊值，其更一般的表示为 F-Score或 F-Measure：
$F-Score=(α^2+1)\frac{PPV×TPR}{α^2PPV+TPR}$
其中α为对TPR与PPV的加权求和。召回率与精确度一样重要时，令α=1，即为 $F_1$ ；当认为精确度重要时，令α<1；反之认为召回率重要些时，则令α>1。

特效度（specificity）也称 TNR（true negativerate），表示负样本被准确预测，公式为：
$Specificity(TNR)=\frac{TN}{TN+FP}$
特效度与误判率成反比，在检测中特效度低，则说明部分样本原本是负样本被模型误判成了缺陷。

假阳性率（false positive rate, FPR），又称误检率，虚警率：
$FPR=\frac{FP}{TN+FP}$
假阴性率（false negative rate, FNR），又称漏检率，漏警率：
$FNR=\frac{FN}{TN+TP}$
准确率（accuracy, ACC），一般情况下，ACC 越高模型越好，但样本不平衡时，ACC 不能很好地评估模型性能。
$C=\frac{T P+T N}{T P+F P+T N+F N}$
平衡准确率(balanced accuracy,BA)：
$BA=\frac{FN}{TN+TP}$
马修斯相关系数 （ Matthews correlation coefficient, MCC）综合了 TPR、TNR、FPR、FNR，是一种比较全面的指标，可以评估样本不平衡下的缺陷检测模型性能。
$C=\frac{T P \times T N-F P \times F N}{\sqrt{(T P+F P)(T P+F N)(T N+F P)(T N+F N)}}$
mAP(mean average precision)是指各个类别预测正确的样本数占总样本数的平均值，越大越好。mAP 中的“AP(average precision)”是指平均精确度。当n=2时，则为二分类问题。当遇到多分类问题时n=类别数+1，因为需要加上背景。
$mAP=\frac{\sum PPV}{n}$
像素准确率(pixel accuracy, PA)，常用于语义分割判断分对的像素数量占总像素数量的比率：
$A=\frac{\sum_{i=0}^{k} p_{i i}}{\sum_{i=0}^{k} \sum_{j=0}^{k} p_{i j}}$
平均像素准确率（mean pixel accuracy, mPA），是对 PA 求平均。
$A=\frac{1}{k+1} \sum_{i=0}^{k} \frac{p_{i i}}{\sum_{i=0}^{k} p_{i j}}$
平均交并比（mean intersection over union, mIoU）表示标注的准确性。
$U=\frac{1}{k+1} \sum_{i=0}^{k} \frac{p_{i i}}{\sum_{i=0}^{k} p_{i j}+\sum_{j=0}^{k} p_{j i}-p_{i i}}$
PA、mPA、mIoU 都为判断语义分割准确率的指标，其中 k 为总类别数， k+1 为加上背景， $P_{ij}$ 为第 $i$ 类像素被判为 $j$ 类的数量， $P_{ij}$ 、 $P_{ii}$ 的含义以此类推。

1.1.3 回归问题

其中， $y^{(i)}$ 和 $\widehat{y}^{(i)}$ 分别表示第 $i$ 个样本的真实值和预测值， $m$ 为样本个数。

（1）均方误差MSE ( Mean Square Error，MSE ) 好求导，曲线比较平滑，使用最多。
$\widehat{y})=\frac{1}{m} \sum_{i=1}^{m}\left(y^{(i)}-\widehat{y}^{(i)}\right)^{2}$
（2）均方根误差RMSE ( Root Mean Square Error,RMSE )
$\widehat{y})=\sqrt{\frac{1}{m} \sum_{i=1}^{m}\left(y^{(i)}-\widehat{y}^{(i)}\right)^{2}}$
（3）平均绝对误差 ( Mean Absolute Error,MAE )
$\operatorname{MAE}(y, \widehat{y})=\frac{1}{m} \sum_{i=1}^{n}\left|y^{(i)}-\widehat{y}^{(i)}\right|$
（4）R方 ( RSquared(r2score) ) 越接近于1，说明模型拟合得越好
$R^{2}(y, \widehat{y})=1-\frac{\sum_{i=0}^{m}\left(y^{(i)}-\widehat{y}^{(i)}\right)^{2}}{\sum_{i=0}^{m}\left(y^{(i)}-\bar{y}\right)^{2}}=\frac{\mathrm{SSR}}{\mathrm{SST}}=1-\frac{\mathrm{SSE}}{\mathrm{SST}}$

$R^{2}(y, \widehat{y})=1-\frac{\sum_{i=0}^{m}\left(y^{(i)}-\widehat{y}^{(i)}\right)^{2} / m}{\sum_{i=0}^{m}\left(y^{(i)}-\bar{y}\right)^{2} / m}=1-\frac{\mathrm{MSE}}{\mathrm{Var}}$

其中，
$\begin{aligned} S S R &=\sum_{i=0}^{m}\left(\widehat{y}^{(i)}-\bar{y}\right)^{2} \\ S S E &=\sum_{i=0}^{m}\left(y^{(i)}-\widehat{y}^{(i)}\right)^{2} \\ S S T &=\sum_{i=0}^{m}\left(y^{(i)}-\bar{y}\right)^{2} \end{aligned}$

1.2 梯度下降

CSDN上高赞的博文：梯度下降算法原理讲解——机器学习

同时更新参数！！！

主要目的：通过迭代找到目标函数的最小值，或者收敛到最小值。

批量梯度下降（Batch Gradient Descent,BGD）：梯度下降的每一步中，都用到了所有的训练样本。
随机梯度下降（Stochastic Gradient Descent,SGD）：梯度下降的每一步中，用到随机一个样本，在每一次计算之后便更新参数，而不需要首先将所有的训练集求和。
小批量梯度下降（Mini-Batch Gradient Descent,MBGD）：梯度下降的每一步中，用到了一定批量的训练样本。

在小批量梯度下降MBGD中：

b=1，等价于随机梯度下降SGD；

b=m，等价于批量梯度下降BGD（m是样本总数）；

b=batch_size，通常是2的指数倍，常见有32，64，128等，是小批量梯度下降MBGD。

参数更新：

都是一直在**repeat（重复）**以下公式：
$w_j:=w_j-\alpha \cdot \frac{\partial J(w)}{\partial w_j}~~~~(\alpha是学习率,~\alpha \cdot \frac{\partial J(w)}{\partial w_j}是梯度即偏导结果)\\(同步更新w_j,(j=0,1,...n))$

但是在实际应用中，并没有更新 $w_0$ ，好像是因为 $w_0=1$ ，还是说是因为要正则化，所以在下列梯度中， $w_0=1$ 是单独更新的，它的梯度后面没有加上 $\frac{λ}{m}{w_0}$ 。

1.批量梯度下降法BGD中梯度为：对所有样本进行**求和 $\sum{}$ **
$\frac{\partial J(w)}{\partial w_j}=\frac{1}{m} \sum_{i=0}^{m}\left(\left(h\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{j}^{(i)}\right)\\ 即~~w_j:=w_j-\alpha\cdot \frac{1}{m} \sum_{i=0}^{m}\left(\left(h\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{j}^{(i)}\right)~~~~(同步更新w_j,(j=0,1,...n))$

BGD当加入正则项后，梯度为：

$w_0:=w_0-\alpha\cdot \frac{1}{m} \sum_{i=1}^{m}\left(\left(h\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{0}^{(i)}\right) \\w_j:=w_j-\alpha\cdot \frac{1}{m} \sum_{i=1}^{m}\left(\left(h\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{j}^{(i)}\right)+\frac{λ}{m}w_j \\(同步更新w_j,(j=1,...n))$
损失函数添加正则项后的SGD、MBGD的变化与BGD类似，后面再加上一个正则项即可。

2.随机梯度下降SGD中梯度为：（选的任一样本做偏导，没有对所有样本进行求和）
$w_j:=w_j-\alpha\cdot\left(\left(h\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{j}^{(i)}\right)$

3.小批量梯度下降BGD中梯度为：（每计算常数b次训练实例，便更新一次参数w）
$w_{j}:=w_{j}-\alpha \frac{1}{b} \sum_{k=i}^{i+b-1}\left(h\left(x^{(k)}\right)-y^{(k)}\right) x_{j}^{(k)}$

1.3 最小二乘法LSM （正规法）

最小二乘法的需要求解最优参数 $w^{*}$ ：

已知：线性回归的目标函数

$J\left( w \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {h}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}}$

其中： ${h}\left( x \right)={w^{T}}X={w_{0}}{x_{0}}+{w_{1}}{x_{1}}+{w_{2}}{x_{2}}+...+{w_{n}}{x_{n}}$

将向量表达形式转为矩阵表达形式，则有 $)=\frac{1}{2}{{\left( Xw -y\right)}^{2}}$ ，其中 $X$ 为 $m$ 行 $n + 1$ 列的矩阵（ $m$ 为样本个数， $n$ 为特征个数）， $w$ 为 $n + 1$ 行1列的矩阵(包含了 $w_0$ )， $y$ 为 $m$ 行1列的矩阵，则可以求得最优参数 $w^{*} ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y$ 。

梯度下降与最小二乘法的比较：

梯度下降：需要选择学习率 $\alpha$ ，需要多次迭代，当特征数量 $n$ 大时也能较好适用，适用于各种类型的模型。

最小二乘法：不需要选择学习率 $\alpha$ ，一次计算得出，需要计算 ${{\left( {{X}^{T}}X \right)}^{-1}}$ ，如果特征数量 $n$ 较大则运算代价大，因为矩阵逆的计算时间复杂度为 $O(n^3)$ ，通常来说当** $n$ 小于10000** 时还是可以接受的，只适用于线性模型，不适合逻辑回归模型等其他模型。

1.4 激活函数

sigmoid函数

sigmoid函数是二分类问题最常用的激活函数，图像为一个S形，结果总是判定为0或1。
$\sigma(z)=g(z)=\frac{1}{1+e^{-z}} \quad Z=w^{T} x+b\\ g'(z)=g(z)(1-g(z))$

逻辑回归是最常见的二分类算法，它的假设函数是采用的极大似然法。
$L(\hat{y}, y)=-y \log (\hat{y})-(1-y) \log (1-\hat{y})$

1.5 函数定义

经常听见目标函数、损失函数、代价函数、假设函数（模型函数），但是很容易搞混淆。

参考CSDN博文：《机器学习-小知识点》3：目标函数、损失函数、代价函数有什么区别？

上述博文参考的知乎文章：机器学习中的目标函数、损失函数、代价函数有什么区别？

本文讲了以下内容：

首先给出结论：损失函数和代价函数是同一个东西，目标函数是一个与他们相关但更广的概念，对于目标函数来说在有约束条件下的最小化就是损失函数（loss function）。
目标函数 = 经验风险最小化 + 结构风险最小化。（经验风险表示拟合程度，结构风险表示模型复杂度）
损失函数越小，拟合越好；平均损失作为经验风险；所以经验风险（3）<（2）<(1)；
结构风险是专门衡量模型复杂度。本题看 $x$ 的最高次数，结构风险（1）< (2) <(3);
所以，(2) $f_2$ 达到了二者的良好平衡，最适合用来预测未知数据集。
目标函数是最终需要优化的函数，其中包括经验风险和结构风险。

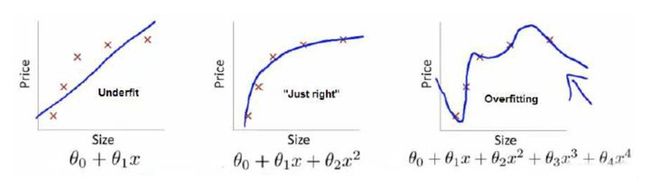
真实值：上图中红叉 × 。（表示代价函数中的 $Y$ ）

预测值：上图的模型函数（即蓝线）依次为 $f_1(x)$ , $f_2(x)$ , $f_3(x)$ 。我们是想用这三个函数分别来拟合Price，Price的真实值记为 $Y$ 。

损失函数( loss function )， $L (Y, f (X))$ ，也叫做代价函数( cost fuunction )：用来度量拟合的程度的函数。损失函数越小，则表示模型拟合得越好。本文中定义的损失函数为： $L(Y, f(X))=(Y-f(X))^{2}$ 。

经验风险：风险函数是损失函数的期望。 $f (X)$ 关于训练集的平均损失称作经验风险（empirical risk），即 $\frac{1}{N} \sum_{i=1}^{N} L\left(y_{i}, f\left(x_{i}\right)\right)$ 。

结构风险 $J (f (x))$ ：用来度量模型的复杂度的函数。在机器学习中也叫做正则化（regularization）。常用的有 $L_1$ ， $L_2$ 范数。

目标函数：最终的优化函数，即最优化经验风险和结构风险。
$\min \frac{1}{N} \sum_{i=1}^{N} L\left(y_{i}, f\left(x_{i}\right)\right)+\lambda J(f)~~~~~~~(λ是正则化参数)$

1.6 正则化

目的：防止过拟合（过拟合就是太精准了，使得泛化性低）。

（1） $L_2$ 正则化（更常用），二范数：

$\frac { 1 } { 2 } \sum _ { i = 1 } ^ { m } ( h _ { w} ( x ^ { ( i ) } ) - y ^ { ( i ) } ) ^ { 2 } + \lambda \sum _ { j = 1 } ^ { n } w_ { j } ^ { 2 }$ ，此时称作Ridge Regression（岭回归）。

（2） $L_1$ 正则化，一范数：

$\frac { 1 } { 2 } \sum _ { i = 1 } ^ { m } ( h _ { w} ( x ^ { ( i ) } ) - y ^ { ( i ) } ) ^ { 2 } + \lambda \sum _ { j = 1 } ^ { n } | w _ { j } |$ ，此时称作Lasso Regression （Lasso回归）。

逻辑回归的目标函数：（对代价函数进行了正则化，最右边加的就是正则项，当λ上升时，方差降低，即越稳定）
$J(w)=\frac{1}{m} \sum_{i=1}^{m}\left[-y^{(i)} \log \left(h\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right) \log \left(1-h\left(x^{(i)}\right)\right)\right]+\frac{\lambda}{2 m} \sum_{j=1}^{n} w_{j}^{2}$

（3）Dropout正则化（常用于深度学习的神经网络中）

类似于 $L_2$ ，与 $L_2$ 正则化不同的是，被应用的方式不同，dropout也会有所不同，甚至更适用于不同的输入范围。

keep-prob=1（没有dropout） keep-prob=0.5（常用取值，保留一般神经元）

在训练阶段使用，在测试阶段不使用！

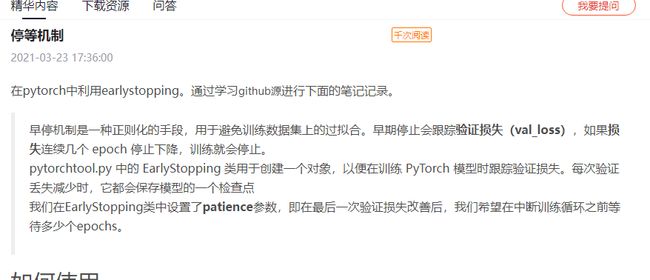
（4）Early stopping早停：代表提早停止训练神经网络

优点：只运行一次梯度下降，你可以找出w的较小值，中间值和较大值，而无需尝试 $L_2$ 正则化超级参数 $\lambda$ 的很多值。

（5）数据增强Data augmentation

随意翻转和裁剪、扭曲变形图片

1.7 方差Variance和偏差Bias

方差Variance：描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，数据的分布就越分散。

偏差Bias：描述的是预测值（估计值）的期望与真实值之间的差距。偏差越大，越偏离真实数据。

一般来说，随着模型复杂度的增加，方差会逐渐增大，偏差会逐渐减小。

训练集误差和交叉验证集误差近似时：偏差/欠拟合
交叉验证集误差远大于训练集误差时：方差/过拟合

1.8 标准化/归一化

目的：提升模型精度、加快模型收敛。

1.归一化（最大-最小规范化）、特征缩放
$x^{*}=\frac{x-x_{\min }}{x_{\max }-x_{\min }}~~~~(将数据映射到[0,1]区间)$
数据归一化的目的是：使得各特征对目标变量的影响一致，会将特征数据进行伸缩变化，所以数据归一化是会改变数据分布的。

2.Z-Score标准化
$x^{*}=\frac{x-\mu}{\sigma}~~(处理后的数据均值为0，方差为1)\\ \begin{aligned} \sigma^{2} &=\frac{1}{m} \sum_{i=1}^{m}\left(x^{(i)}-\mu\right)^{2}~~~~方差 \\ \mu &=\frac{1}{m} \sum_{i=1}^{m} x^{(i)}~~~~均值 \end{aligned}$
数据标准化为了不同特征之间具备可比性，经过标准化变换之后的特征数据分布没有发生改变。

就是当数据特征取值范围或单位差异较大时，最好是做一下标准化处理。

1.9 归一化层和归一化

参考博文：BatchNormalization、LayerNormalization、InstanceNorm、GroupNorm、SwitchableNorm总结

1.10 k-means

5 分钟带你弄懂 K-means 聚类 - 打工人小飞的文章 - 知乎：https://zhuanlan.zhihu.com/p/357072839

跟knn很像，但是knn是监督学习，k-means是无监督学习（精度会低一些）。

k-means属于无监督学习的一种。物以类聚，人以群分。

如果某些样本非常相似，则把它们归为一类。再用这些样本的中心位置表示类别，以方便其他样本的加入。

每当这个类别中有了新的相似样本加入，就要更新该类别的中心位置，以方便新样本去适应这个类别。

在数学中，通常用距离去衡量两个样本的相似程度，即用欧氏距离去适应。

引入cluster概念表示类别（簇）。中心坐标用centroid表示。

对于k的设计很敏感，k就是类别个数。

1.11 协方差

定义一个表示X, Y 相互关系的数字特征，也就是协方差： $co v (X, Y) = E (X - EX) (Y - E Y)$ 。

当 cov(X, Y)>0时，表明 X与Y 正相关；

当 cov(X, Y)<0时，表明 X与Y 负相关；

当 cov(X, Y)=0时，表明 X与Y 不相关。

这就是协方差的意义。

1.12 早停

就是比如你设置100轮早停，就是在获得最好的map后，后面的100轮相对这个最好的map都是下降的，就停止训练。

1.x 一些统计学知识

似然函数：（是连乘的，不好计算）
$L(w)=\prod_{i=1}^{m} P\left(y^{(i)} \mid x^{(i)} ; w\right)=\prod_{i=1}^{m}\left(h\left(x^{(i)}\right)\right)^{y^{(i)}}\left(1-h\left(x^{(i)}\right)\right)^{1-y^{(i)}}$
似然函数两边取对数，则连乘号变成了连加号：
$l(w)=logL(w)=\sum_{i=1}^{m}\left(y^{(i)} \log \left(h\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right) \log \left(1-h\left(x^{(i)}\right)\right)\right)$

2 代码积累

2.1 基本流程

[1] 读取文件：

import pandas as pd
import numpy as np

path = 'data/regress_data2.csv'	# 文件路径
data2 = pd.read_csv(path)	# 读取DataFrame数据
data2.head()	# 打印数据前5行信息
data2.describe()	# 打印数据的一些基本信息，如最大值、均值等

[2] 当特征比较多时，进行特征归一化 or 标准化：

data2 = (data2 - data2.mean()) / data2.std() # 标准化

[3] 数据预处理步骤：

# add ones column
data2.insert(0, 'Ones', 1)	# 为了特征向量化，手动添加一列w0，全部置为1

# set X (training data) and y (target variable)	# 切片，分割成X训练集和Y目标值
cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
y2 = data2.iloc[:,cols-1:cols]

# convert to matrices and initialize theta	# 转换成矩阵、初始化θ
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
w2 = np.matrix(np.array([0,0,0]))

# perform linear regression on the data set # 对数据集执行线性回归
g2, cost2 = batch_gradientDescent(X2, y2, w2, alpha, iters)

# get the cost (error) of the model	# 获取模型的代价（错误）
computeCost(X2, y2, g2)

[4] 绘制训练进程：

fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost2, 'r')
ax.set_xlabel('迭代次数', fontsize=18)
ax.set_ylabel('代价', rotation=0, fontsize=18)
ax.set_title('误差和训练Epoch数', fontsize=18)
plt.show()

3 sklearn

Scikit-learn是基于 Python 语言的机器学习工具，它建立在 NumPy、SciPy、Pandas和Matplotlib之上，被广泛地用于统计分析和机器学习建模等数据科学领域。

Sklearn 中文文档：https://sklearn.apachecn.org/#/

黄海广老师的ML-lesson3-Scikit-learn.ipynb文件中有教程，需要的时候可以再去详细看一下。

做人工智能课设的时候采用的数据集：UCI数据集

3.1 基本建模流程

基本建模的符号标记：

符号	代表含义	符号	代表含义
X_train	训练数据	y_train	训练集标签
X_test	测试数据	y_test	测试集标签
X	完整数据	y	数据标签
		y_pred	预测标签

3.1.1 导入工具包的方法如下(这里使用伪代码)：

from sklearn import 包名称
from sklearn.库名称 import 包名称

from sklearn import datasets, preprocessing  
#导入数据集，数据预处理库  
from sklearn.model_selection import train_test_split    
#从模型选择库导入数据切分包  
from sklearn.linear_model import LinearRegression    
#从线性模型库导入线性回归包  
from sklearn.metrics import r2_score  
#从评价指标库导入R2评价指标

3.1.2 导入skearn自带数据集

Scikit-learn支持以NumPy的arrays对象、Pandas对象、SciPy的稀疏矩阵及其他可转换为数值型arrays的数据结构作为其输入，前提是数据必须是数值型的。

sklearn.datasets模块提供了一系列加载和获取著名数据集如鸢尾花、波士顿房价、Olivetti人脸、MNIST数据集等的工具，也包括了一些toy data如S型数据等的生成工具。

#导入内置的鸢尾花数据
from sklearn.datasets import load_iris

iris = load_iris()	# 加载鸢尾花数据集
#定义数据、标签
X = iris.data
y = iris.target

3.2 数据预处理

3.2.1 数据划分

机器学习的数据，可以划分为训练集、验证集和测试集，也可以划分为训练集和测试集。

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X,
                                                    y,
                                                    random_state=12,
                                                    stratify=y,
                                                    test_size=0.3)
#将完整数据集的70%作为训练集，30%作为测试集，
#并使得测试集和训练集中各类别数据的比例与原始数据集比例一致(stratify分层策略)，另外可通过设置shuffle=True 提前打乱数据。

3.2.2 数据变换操作

预处理操作	库名称
标准化	StandardScaler
最小最大标准化	MinMaxScaler
One-Hot编码	OneHotEncoder
归一化	Normalizer
二值化(单个特征转换)	Binarizer
标签编码	LabelEncoder
缺失值填补	Imputer
多项式特征生成	PolynomialFeatures

#使⽤Scikit-learn进⾏数据标准化
from sklearn.preprocessing import StandardScaler

#构建转换器实例
scaler = StandardScaler( )

#拟合及转换
scaler.fit_transform(X_train)

3.2.3 特征选择

感觉有点不清楚，先带过~

3.3 监督学习

3.3.1 回归

回归模型名称	库名称
线性回归	LinearRegression
岭回归 L2	Ridge
LASSO回归 L1	LASSO
ElasticNet回归	ElasticNet
决策树回归	tree.DecisionTreeRegressor

#从线性模型库导入线性回归模型
from sklearn.linear_model import LinearRegression
# 构建模型实例
lr = LinearRegression(normalize=True)
# 训练模型
lr.fit(X_train, y_train)
# 作出预测
y_pred = lr.predict(X_test)

3.3.2 分类

模型名称	库名称
逻辑回归	linear model.LogisticRearession
支持向量机	svm.SVC
朴素贝叶斯	naïve_bayes.GaussianNB
KNN	neighbors.NearestNeighbors
随机森林	ensemble.RandomForestClassifier
GBDT	ensemble.GradientBoostingClassifier

#从树模型库导入决策树
from sklearn.tree import DecisionTreeClassifier
#定义模型
clf = DecisionTreeClassifier(max_depth=5)
#训练模型
clf.fit(X_train, y_train)
#使用决策树分类算法解决二分类问题，得到的是类别
y_pred = clf.predict(X_test)
#y_prob 为每个样本预测为“0”和“1”类的概率
y_prob = clf.predict_proba(X_test)

3.4 无监督学习算法

3.4.1 聚类算法

模型名称	库名称
K-means	KMeans
DBSCAN	DBSCAN
层次聚类	AgglomerativeClustering
谱聚类	SpectralClustering

#从聚类模型库导入kmeans  
from sklearn.cluster import KMeans  
#构建聚类实例  
kmeans = KMeans(n_clusters=3, random_state=0)  
#拟合  
kmeans.fit(X_train)  
#预测  
kmeans.predict(X_test)

3.4.2 降维算法

最常见的降维方法是PCA(主成分分析)。

#导入PCA库
from sklearn.decomposition import PCA
#设置主成分数量为3，n_components代表主成分数量
pca = PCA(n_components=3)
#训练模型
pca.fit(X)
#投影后各个特征维度的方差比例(这里是三个主成分)
print(pca.explained_variance_ratio_)
#投影后的特征维度的方差
print(pca.explained_variance_)

3.5 评价指标

sklearn.metrics模块包含了一系列用于评价模型的评分函数、损失函数以及成对数据的距离度量函数。

评价指标主要分为分类评价指标、回归评价指标等等，这里列举了常见的几种评价指标。

评价指标	库名称	使用范围
正确率	accuracy_score	分类
精确率	precision_score	分类
F1 值	f1_score	分类
对数损失	log_loss	分类
混淆矩阵	confusion_matrix	分类
含多种评价的分类报告	classification_report	分类
均方误差MSE	mean_squared_error	回归
平均绝对误差MAE	mean_absolute_error	回归
决定系数R2	r2_score	回归

#从评价指标库导入准确率
from sklearn.metrics import accuracy_score
#计算样本的准确率
accuracy_score(y_test, y_pred)
#对于测试集而言，大部分函数都必须包含真实值y_test和预测值y_pred

3.6 交叉验证及超参数调优

♥3.6.1 交叉验证

这代码挺好的，又能训练，又能评价，人工智能课设里面大多数就是这种的代码。

此外，Scikit-learn提供了部分带交叉验证功能的模型类如LogisticRegressionCV、LassoCV、等，这些类包含CV参数（表示分成几折进行验证）。

#从模型选择库导入交叉验证分数  
from sklearn.model_selection import cross_val_score    
clf = DecisionTreeClassifier(max_depth=5)  
#使用5折交叉验证对决策树模型进行评估，使用的评分函数为F1值  
scores = cross_val_score(clf, X_train, y_train,cv=5, scoring='f1_weighted')

3.6.2 超参数调优

在机器学习中，超参数是指无法从数据中学习而需要在训练前提供的参数。机器学习模型的性能在很大程度上依赖于寻找最佳超参数集。

超参数调整一般是指调整模型的超参数，这基本上是一个非常耗时的过程。

目前主要有 3 种最流行的超参数调整技术：网格搜索、随机搜索和贝叶斯搜索，其中Scikit-learn内置了网格搜索、随机搜索。

网格搜索：

#从模型选择库导入网格搜索
from sklearn.model_selection import GridSearchCV
from sklearn import svm

svc = svm.SVC()
#把超参数集合作为字典
params = {'kernel': ['linear', 'rbf'], 'C': [1, 10]}
#进行网格搜索，使用了支持向量机分类器，并进行五折交叉验证
grid_search = GridSearchCV(svc, params, cv=5)
#模型训练
grid_search.fit(X_train, y_train)
#获取模型最优超参数组合
grid_search.best_params_

随机搜索：

#从模型选择库导入随机搜索
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint

svc = svm.SVC()
#把超参数组合作为字典
param_dist = {'kernel': ['linear', 'rbf'], 'C': randint(1, 20)}
#进行随机搜索
random_search = RandomizedSearchCV(svc, param_dist, n_iter=10)
#模型训练
random_search.fit(X_train, y_train)
#获取最优超参数组合
random_search.best_params_

4 卷积神经网络CNN

4.1 AlexNet网络

参考博文：深入理解AlexNet网络

第一个典型的CNN是LeNet5网络结构，但是第一个引起大家注意的网络却是AlexNet，也就是文章《ImageNet Classification with Deep Convolutional Neural Networks》介绍的网络结构。这篇的论文第一作者是Alex，所以网络结构称为AlexNet。

AlexNet有60 million个参数和65000个神经元，五层卷积，三层全连接网络，最终的输出层是1000通道的softmax。

LabelMe(Labelme: a database and web-based tool for image annotation. )，包含了成百上千的全分割图像。
ImageNet(ImageNet: A Large-Scale Hierarchical Image Database. I),包含15 million 标记的高分辨率图像，包含超过了22000种现实中的事物。

4.2 层的作用

参考博文：卷积神经网络中卷积层、池化层、全连接层的作用

参考博文2：从卷积层、激活层、池化层到全连接层深度解析卷积神经网络的原理

我们应该把神经元和神经元之间的连接的权重个数降下来，但是降下来我们又不能保证它有较强的学习能力，所以这是一个纠结的地方，所以有一个方法就是局部连接+权值共享。卷积神经网络就是局部连接+权值共享的神经网络。

流程一般是：数据输入的是一张图片（输入层），CONV表示卷积层，RELU表示激励层，POOL表示池化层，Fc表示全连接层。

4.2.1 输入层

在图片输出到神经网络之前，常常先进行图像处理，有三种常见的图像的处理方式：

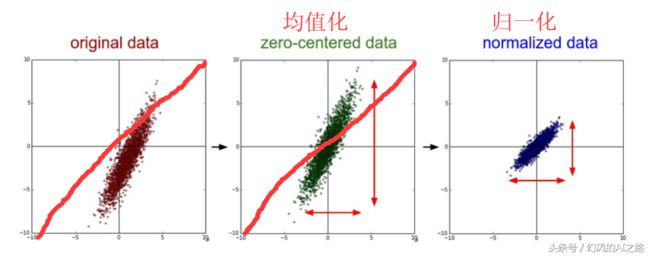
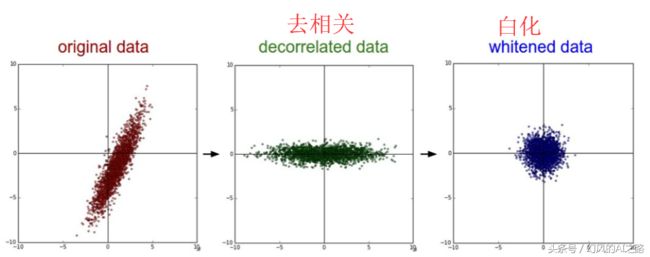
均值化：把输入数据各个维度都中心化到0，所有样本求和求平均，然后用所有的样本减去这个均值样本就是去均值。
归一化：数据幅度归一化到同样的范围，对于每个特征而言，范围最好是[-1,1]
PCA/白化：用PCA降维，让每个维度的相关度取消，特征和特征之间是相互独立的。白化是对数据每个特征轴上的幅度归一化

均值化和归一化

去相关和白化

4.2.2 卷积层CONV

卷积核越大，receptive field（感受野）越大，看到的图片信息越多，因此获得的特征越好。虽说如此，但是大的卷积核会导致计算量的暴增，不利于模型深度的增加，计算性能也会降低。

卷积核是算法自己学习得到的，它会和上一层计算，比如，第二层的0节点的数值就是局部区域的线性组合（w1* 0+w2 *1+w3 *4+w4 *5），即被圈中节点的数值乘以对应的权重后相加。

卷积层的作用是提取输入图片中的信息，这些信息被称为图像特征，这些特征是由图像中的每个像素通过组合或者独立的方式所体现，比如图片的纹理特征，颜色特征。

比如下面这张图片，蓝色框框住的地方就是脸部特征，这些特征其实是由一个个像素所组成的。

再者这是一张彩色图片，它包含R、G、B三个通道，这里就不多赘述RGB颜色空间了，即红色、绿色、蓝色三个通道叠加而成，每个通道其实也相当于一张单通道的图片，这张三通道的图片的特征是由这三个通道的特征组合而成。

那么卷积层是如何通过运算提取图片特征的呢？

卷积操作类似于数学中的卷积（应该是内积吧？），但是更加简单，计算机和我们看到的图像不一样，计算机看到的图像其实就是一个个矩阵，一系列数字，图像有几个通道就由几个矩阵相加而成的。

这里的卷积操作是通过卷积核对每个通道的矩阵从左到右（卷积核一般是3x3的矩阵）从上至下进行互相关运算（先是从左到右，再是从上至下，所以卷积操作也会保留位置信息），就像一个小的窗口一样，从左上角一步步滑动到右下角，滑动的步长是个超参数，互相关运算的意思就是对应位置相乘再相加，最后把三个通道的值也对应加起来得到一个值。

图像卷积运算如下图所示：

卷积层中最重要的是卷积核（训练出来的），不同的卷积核可以探测特定的形状、颜色、对比度等，然后特征图保持了抓取后的空间结构，所以不同卷积核对应的特征图表示某一维度的特征，具体什么特征可能我们并不知道。特征图作为输入再被卷积的话，可以则可以由此探测到"更大"的形状概念，也就是说随着卷积神经网络层数的增加，特征提取的越来越具体化。

4.2.3 激励层RELU

激励层的作用可以理解为把卷积层的结果做非线性映射。（f是激活函数）

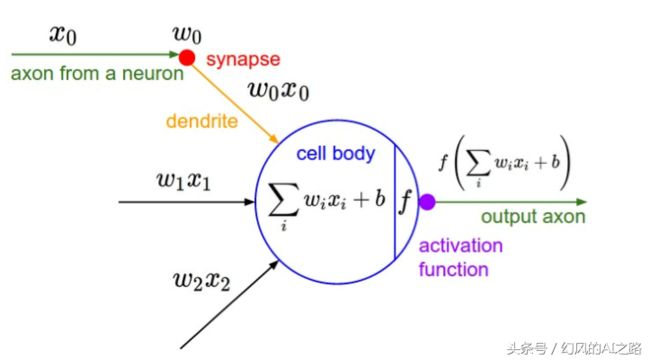
一般不要用sigmoid，首先试RELU，因为快，但要小心点，如果RELU失效，请用Leaky ReLU，某些情况下tanh倒是有不错的结果。

4.2.4 池化层POOL

池化层的作用是对卷积层中提取的特征进行挑选。

池化层夹在连续的卷积层中间，压缩数据和参数的量，减小过拟合，池化层并没有参数，它只不过是把上层给它的结果做了一个下采样（数据压缩）。常见的池化操作有最大池化和平均池化，池化层是由n×n大小的矩阵窗口滑动来进行计算的，类似于卷积层，只不过不是做互相关运算，而是求n×n大小的矩阵中的最大值和平均值。

最大池化主要是用于提取目标的特征信息，而平均池化则更加注重于对背景特征信息的提取。

如图，对特征图进行最大池化操作：

池化层主要有以下几个作用：

挑选不受位置干扰的图像信息。
对特征进行降维，提高后续特征的感受野，也就是让池化后的一个像素对应前面图片中的一个区域。
因为池化层是不进行反向传播的，而且池化层减少了特征图的变量个数，所以池化层可以减少计算量。

4.2.5 全连接层Fc(dense)

池化层的后面一般接着全连接层，全连接层将池化层的所有特征矩阵转化成一维的特征大向量，全连接层一般放在卷积神经网络结构中的最后，用于对图片进行分类到了全连接层，我们的神经网络就要准备输出结果了。

如下图所示，倒数第二列的向量就是全连接层的数据：

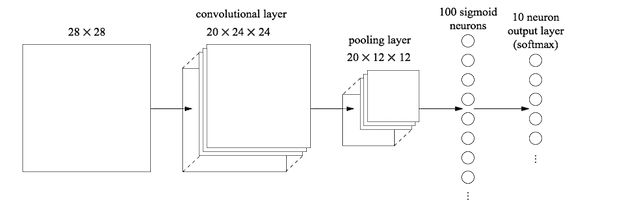
从池化层到全连接层会进行池化操作，数据会进行多到少的映射，进行降维，也就是为什么上图从20×12×12变成100个神经元了，数据在慢慢减少，说明离输出结果越来越近，从全连接层到输出层会再一次减少数据，变成更加低维的向量，这个操作一般叫做softmax，这个向量的维度就是需要输出的类别数。

因为从卷积层过来的数据大多了，全连接层的作用主要是对数据进行降维操作，不然数据骤降到输出层，softmax操作可能会丢失一些图像特征的重要信息。

4.3 其他层

4.3.1 归一化层

参考博文：BatchNormalization、LayerNormalization、InstanceNorm、GroupNorm、SwitchableNorm总结

Local Response Normalized：局部响应归一化。

简单来说：对于每个隐层神经元，把逐渐向非线性函数映射后向取值区间极限饱和区靠拢的输入分布强制拉回到均值为0方差为1的比较标准的正态分布，使得非线性变换函数的输入值落入对输入比较敏感的区域，以此避免梯度消失问题。

与激活函数层、卷积层（cnn）、全连接层（FC）、池化层一样，批量归一化也属于网络的一层，简称BN。BN通常用在FC/cnn之后，激活函数层之前，他对FC/cnn的输出的每一维进行归一化（归一化至：均值0、方差为1），然后变换重构后再把数据喂给下一层网络。

BN的好处：

能选择较大的初始学习率，提高训练收敛速度
你再也不用去理会过拟合中drop out、L2正则项参数的选择问题，采用BN算法后，你可以移除这两项了参数，或者可以选择更小的L2正则约束参数了，因为BN自带正则化的特性，能提高网络泛化能力
减少梯度爆炸/消失的出现，特别对于tanh，sigmoid这类会两端饱和的激活函数
减少对参数初始化的依赖，就算参数初始化得不好，在BN的加持下网络还是表现较好

参考博文2：【深度学习】批归一化（Batch Normalization）

BN可以作为神经网络的一层，放在激活函数（如Relu）之前。BN的算法流程如下图：

10 一些实际应用

表面缺陷检测

参考文献：[1]赵朗月,吴一全.基于机器视觉的表面缺陷检测方法研究进展[J/OL].仪器仪表学报:1-22[2022-02-17].http://kns.cnki.net/kcms/detail/11.2179.TH.20220128.1056.008.html.

1.1 提及的缺陷检测技术

$缺陷检测=\left\{\begin{array}{l} 传统图像处理方式\left\{\begin{array}{l} 图像分割\left\{\begin{array}{l}阈值分割\\边缘检测\\区域生长\end{array}\right.\\ 特征提取:颜色、纹理、形状 \end{array}\right.\\ 机器学习\left\{\begin{array}{l} 无监督学习\left\{\begin{array}{l} 聚类:按照一定的规则对样本进行划分，是一种分类问题\\ 无监督特征学习\left\{\begin{array}{l}主成分分析PCA\\稀疏编码法SC\\自编码器AE\end{array}\right.\\ 概率密度估计\left\{\begin{array}{l}生成对抗网络GAN\\变分自编码器VAE\end{array}\right. \end{array}\right.\\ 有监督学习\left\{\begin{array}{l} 非概率模型\left\{\begin{array}{l}多层感知机MLP\\支持向量机SVM\\K近邻KNN\end{array}\right.\\ 概率判别模型\left\{\begin{array}{l}决策树\\逻辑回归\\最大熵模型\\条件随机场\end{array}\right.\\ 生成模型\left\{\begin{array}{l}朴素贝叶斯\\受限玻尔兹曼机\\隐马尔可夫模型\end{array}\right. \end{array}\right. \end{array}\right.\\ 深度学习\left\{\begin{array}{l} 检测网络\left\{\begin{array}{l} 双阶段网络:Faster R-CNN\\ 单阶段网络\left\{\begin{array}{l}SSD\\YOLO\end{array}\right. \end{array}\right.\\ 分割网络\left\{\begin{array}{l} 语义分割\left\{\begin{array}{l}FCN\\SegNet\\DeepLab系列\\U-Net\end{array}\right.\\ 实例分割\left\{\begin{array}{l}Mask R-CNN\\图像金字塔卷积神经网络IPCNN\end{array}\right. \end{array}\right.\\ 分类网络(被用于特征提取和分类的Backbone)\left\{\begin{array}{l}VGG\\GoogLeNet\\ResNet是VGG-16的延申，增添了残差单元\end{array}\right. \end{array}\right. \end{array}\right.$

表面缺陷的检测定义

缺陷的检测，通常是指对物体表面的缺陷进行检测，可采用传统的图像处理算法，也可使用先进的机器学习技术，不管采用哪种方法，其目的都是对工件表面的斑点、裂痕、腐蚀、残缺等进行检测。在对缺陷进行检测时包含 3 个方面：第一，需要对其进行识别分类，判断是否为缺陷并区分缺陷的类型；第二，定位缺陷，给出其位置信息；第三，对其进行分割，确定其形状、尺寸。

使用传统方法进行处理

一般步骤为：图像采集、图像预处理（去噪、增强等）、图像分割、特征提取及分类识别。在此部分，主要概括了图像分割和特征提取两个方面，其中图像分割包含阈值分割、边缘检测和区域生长；特征提取则从颜色、纹理、形状 3个角度进行概括。

检测网络

依据网络中是否含有候选框，将网络分为单阶段和双阶段。单阶段网络中输入图像、输出备选框与分类是在一体化完成的；而双阶段网络中一半选择备选框，一半对备选框进行判断，两者之间进行级联。

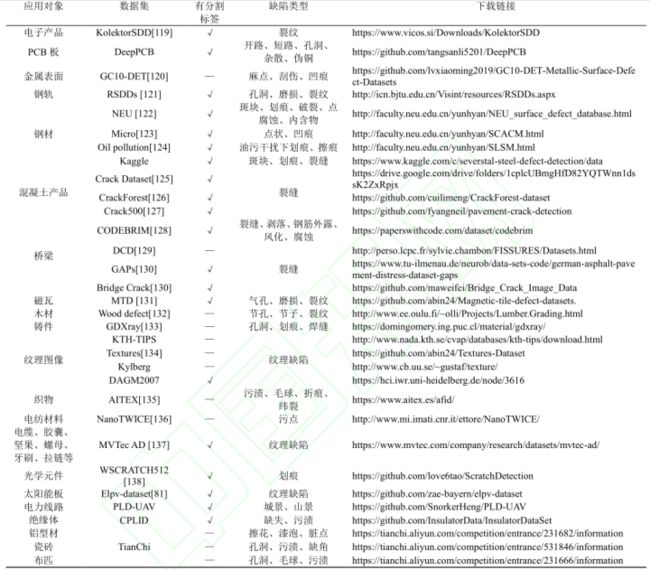
1.2 30种工业缺陷数据集

没写完，太多了，自己到时候看论文去。

应用对象	数据集	是否带有分割标签	缺陷类型	下载地址
电子产品	KolektorSDD	√	裂纹	https://www.vicos.si/Downloads/KolektorSDD
PCB板	DeepPCB	√	开路、短路、孔洞、杂散、伪铜	https://github.com/tangsanli5201/DeepPCB
金属表面	GC10-DET	一	麻点、刮伤、凹痕	https://github.com/lvxiaoming2019/GC10-DET-Metallic-Surface-Defect-Datasets
钢轨	RSDDs	√	孔洞、磨损、裂纹	http://icn.bjtu.edu.cn/Visint/resources/RSDDs.aspx
	NEU	√	斑块、划痕、破裂、点腐蚀、内含物	http://faculty.neu.edu.cn/yunhyan/NEU_surface_defect_database.html
钢材	Micro	√	点状、凹痕	http://faculty.neu.edu.cn/yunhyan/SCACM.html
	Oil pollution	√	油污干扰下划痕、擦痕	http://faculty.neu.edu.cn/yunhyan/SLSM.html
	Kaggle	√	斑块、划痕、裂缝	https://www.kaggle.com/c/severstal-steel-defect-detection/data

xxx 论文

1 一些知识点

1.图像分割任务中是采用的像素级标签，其他任务例如图像分类任务中是采用图像级标签。

2.一般弱监督任务采用的是像素级标签。CAM（Class Activation Mapping，类激活映射）就是目前所有弱监督算法的重要鼻祖。

3.弱监督的通用方案，CAM从图像级标签到像素级标签

4.深度学习笔记：随机种子的作用

深度学习网络模型中初始的权值参数通常都是初始化成随机数
而使用梯度下降法最终得到的局部最优解对于初始位置点的选择很敏感
为了能够完全复现作者的开源深度学习代码，随机种子的选择能够减少一定程度上算法结果的随机性，也就是更接近于原始作者的结果，即产生随机种子意味着每次运行实验，产生的随机数都是相同的。

贡献：

1.为了实现这一点，我们提出了一个具有端到端学习的统一网络，并支持处理粗糙的像素级标签。

问题：

（1）dynamically balanced loss动态平衡损失、 the gradient-flow adjustment梯度调整、the distance transform距离转换分别的作用？

the gradient-flow adjustment梯度调整：防止不稳定的分割特征在早期阶段显著影响分类层的学习。

（2）N是什么？

（3）像素级标记、图像级标记，定义？在本文中用在哪儿的？

答：我们提出了一种具有两个子网络的架构:从像素级标签学习的分割子网络和从弱图像级标签学习的分类子网络。

（4）哪些是分段数据？哪些用于分类？

（5）在评估中，为什么有的class=6？class=10？

（6）在最后面的一些部分中，component（组件）这个词出现的频率很高，是什么意思？难道是分段自网络or分类子网络？

答：就是第（1）个问题提到的3个东西。dynamically balanced loss、gradient-flow adjustment、Spatial label uncertainty（空间标签不确定性，但是好像就是指距离转换）。

（7）the gradient-flow adjustment就是网络结构图中的那个二极管，可是代码中或者算法上是怎么实现的呢？

代码：

1.Pytorch中TensorBoard及torchsummary的使用

tensorboard是在torch中的神经网络可视化工具。

为了能够完全复现作者的开源深度学习代码，随机种子的选择能够减少一定程度上算法结果的随机性，也就是更接近于原始作者的结果，即产生随机种子意味着每次运行实验，产生的随机数都是相同的。

贡献：