Apollo学习笔记（24）基于采样的路径规划算法

之前的文章都是基于搜索的路径算法，这两天在又学习了一下基于采样的路径规划算法，这里做一下记录，最后会奉上大神的链接

基于采样的路径规划算法大致可以分为综合查询方法和单一查询方法两种。

1. 前者首先构建路线图，先通过采样和碰撞检测建立完整的无向图，以得到构型空间的完整连接属性，再通过图搜索即可得到可行的路径。
2. 后者则从特定的初始构型出发局部建立路线图，在构型空间中延伸树型数据结构，最终使它们相连。

其中，综合查询方法的代表性的方法就是概率路线图（Probabilistic Roadmap，PRM），单一查询方法则以快速扩展随机树算法（Rapidly-exploring Random Tree）。下面将对这两种方式都做一个详细的描述。

概率路线图PRM

PRM主要分为两个步骤：

1. 第一步，预处理，讲需要规划的区域处理成一个满足要求的无向图。
2. 第二步，搜索，采用图搜索的方式对无向图进行搜索，如果能找到一条从起始点到终点的路径，则说明存在可行的路径。

预处理的步骤

1. 初始化。设$G(V,E)$为一个无向图，其中顶点集$V$代表无碰撞的构型，连线集$E$代表无碰撞路径。初始状态为空。
2. 构型采样。从构型空间中采样一个无碰撞的点$\alpha (i)$并加入到顶点集$V$中。
3. 领域计算。定义距离$\rho$，对于已经存在于顶点集$V$中的点，如果它与$\alpha (i)$的距离小于$\rho$，则将其称作点$\alpha (i)$的邻域点。
4. 边线连接。将点$\alpha (i)$与其领域点相连，生成连线$\tau$。
5. 碰撞检测。检测连线$\tau$是否与障碍物发生碰撞，如果无碰撞，则将其加入到连线集$E$中。
6. 结束条件。当所有采样点（满足采样数量要求）均已完成上述步骤后结束，否则重复2-5。

搜索

采用图搜索的方式对无向图$G$进行搜索，如果能找到一条从起始点到终点的路线，就说明有可行的路径。

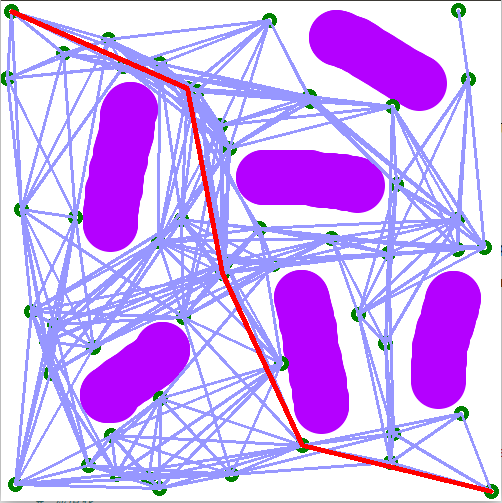
下面结合示意图对整个算法就行说明：

1. 初始化，首先构造地图，如下图所示，图片中，黑色区域为障碍物，白色表示可行驶区间，
   

2. 构型采样，在图中随机采样一定数量的点，并且去掉其中与障碍物有干涉的点，图中最左上角和右下角的点为规划的起点和终点。
   

3. 邻域计算，边线连接与碰撞检测。对每一个点，取其领域内（需要设置邻域的范围，比如点半径为）的所有点进行连线，对连线进行碰撞检测，去掉经过障碍物的连线，将结果存放在邻接矩阵中。
   

4. 使用选择的搜索算法，一般来说选择A*，对上图进行搜索，找到从左上到右下的最短路径，即为目标路径。
   

分析

采样数量的影响

显然，对同一地图，采样点的数量越多，找到合理路径以及更优路径的概率就越大。但同时，采样点数量越多，计算与搜索时间也会更长。

如果只设置10个采样点，邻域200。可以看到，并不能找到可行路径，这也说明了抽样规划算法存在的完备性弱的问题。
而若设置较多采样点，虽然都能找到可行路径，但耗时却会增加很多。

邻域设置的影响

邻域的设置影响着连线的建立与检测。当邻域设置过小，由于连线路径太少，可能找不到解；当领域设置太大，会检测太多较远的点之间的连线，而增加耗时。

如果邻域设置为100，找不到解；设置为1000，耗时4.470s，耗时较长，

快速随机扩展树（RRT）

RRT算法与PRM算法十分类似，都是通过抽样来在已知的地图上建立无向图，进而通过搜索方法寻找相对最优的路径。不同的地方在于，PRM算法在一开始就通过抽样在地图上构建出完整的无向图，再进行图搜索；而RRT算法则是从某个点出发一边搜索，一边抽样并建图。

与PRM算法相同，RRT算法也是概率完备的：只要路径存在，且规划的时间足够长，就一定能确保找到一条路径解。注意“且规划的时间足够长”这一前提条件，说明了如果规划器的参数设置不合理（如搜索次数限制太少、采样点过少等），就可能找不到解。

算法说明

我们可以把RRT算法比较形象地看做“树型算法”。它从一个起始构型（对于二维图，就是一个点）出发，不断延伸树型数据，最终与目标点相连。先放一张规划的结果可能更加便于理解：

算法步骤

1. 初始化，和PRM一样都需要先建一张地图，
   
2. 随机采样

我们已经确定了规划的起始点，按道理它需要不断地向着目标点进行生长。但需要注意的是，由于存在障碍物，如果我们让树型一味朝着目标点延伸，则可能会因为“撞墙”而失败。因此，我们采取了一种随机采样方法：在每次选择生长方向时，有一定的概率会向着目标点延伸，也有一定的概率会随机在地图内选择一个方向延伸一段距离，关键代码如下:

# 利用rand()函数在[0,1]区间内随机生成一个数
if np.random.rand() < 0.5:
    # 如果小于0.5，则在图的范围内随机采样一个点
    sample = np.mat(np.random.randint(0, img_binary.shape[0] - 1, (1, 2)))
else:
    # 否则用目标点作为采样点
    sample = self.point_goal

我们每一步让RRT树有0.5的概率直接采样终点向目标点前进，有0.5的概率向地图内任意方向前进。

3. 生长点选择与碰撞检测

从上图可以看到，由于每次生长都存在一定的随机性，因此RRT树会逐渐出现许多分支，那么每一步中我们该如何选择要延伸哪个分支呢？这里我们直接选择RRT树中离采样点最近的点，并向其延伸。

假设我们采样了空间中随机一个点，接下来从现有的RRT树中选择离采样点最近的一个点，并向采样点延伸一段距离。假如在这段延伸中没有发生碰撞（碰撞检测），而且新点与现有的所有点的距离大于某个判断阈值（防止生长到RRT已经探索过的位置），则将这个新点也加入RRT树。
个人觉得这一步，和A*的代价方程的意义是一样的，要保证总体向着目标移动。

4. 终止条件

由于我们每次延伸的距离是固定的，所以并不能保证最后一次延伸能够刚好到达终点的位置，更可能的情况是在终点周围来回跳动。因此我们设定一个阈值，假如本次延伸的新点与终点的距离小于这个阈值，我们就认为已经规划成功。

下面是随机采样概率0.5，步长20，采样上限20000次的结果

分析

由于RRT算法是概率完备的，预设参数可能对规划结果造成不同的影响，其中最主要的两个参数就是随机采样的概率和生长步长。

随机采样概率

我们每一次采样，都有一定概率朝着任意方向走，或朝着终点走。这个概率显然会影响搜索效果。给人最直接的感觉是，随机采样的概率越大，RRT树的分支也就越多，反之则难以发生新的分支。下面我们修改随机采样概率来看看效果。

设随机采样的概率为0.01，采样上限20000次。可以看到，直到达到采样上限也没有成功找到解。这是因为RRT产生分支的概率太小，经历了许多次碰撞才能凭借分支绕过障碍物。
设随机采样的概率为1.0，采样上限20000次。可以看到，虽然规划得以成功，但由于生长缺乏方向性，其实是一种“碰运气”式的搜索。RRT树的分支填充了所有空间直至找到目标点。这样的搜索会消耗大量的时间。

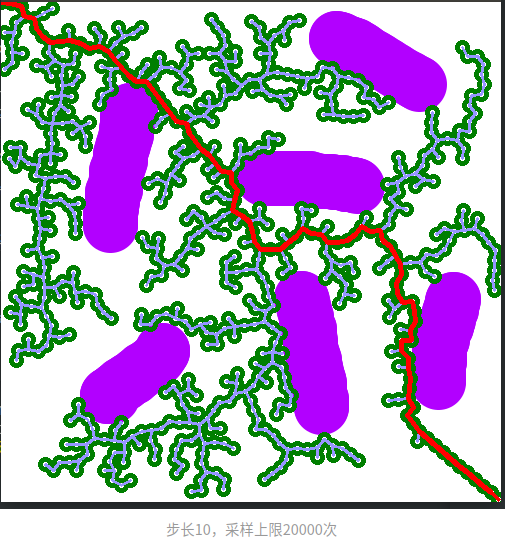
生长步长

我们每一次RRT树的延伸，都有一个固定的步长。这个步长的设置显然也会影响树的形状。当步长太大时，可能由于太过笨拙而无法成功绕过障碍物；当步长过小时，生长的速度显然会有所减慢（因为同样的距离要生长更多次）。一般来说，空间越复杂，步长越小。这里必须注意的是，生长步长一定要比判断是否为同一个采样点的阈值要大。

步长10，采样上限20000次。可以看到，采样点极其密集，消耗的时间更长。
步长200，采样上限20000次。没有搜索到最终结果，可以看到，由于步长太大，生长点在障碍物与终点之间来回跳动，始终不能满足碰撞检测或终止条件的要求。

最后，奉上大神的链接

https://zhuanlan.zhihu.com/p/66047152
https://zhuanlan.zhihu.com/p/65673502
https://www.cnblogs.com/21207-iHome/p/7210543.html