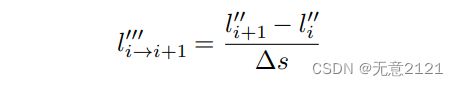Apollo planning之PiecewiseJerkPathOptimizer
目录
1 分段加加速度路径优化概览
1.1 输入,输出代码
1.2 论文摘要
2 优化过程的详细数学理论
2.1 Smooth Driving Guide Line Generation
2.2 Path Planning in a Frenet Frame
2.3 Path Boundary Decision and Computation
2.4 Path Optimization
2.5 Variable Boundary Estimation for Kinematic Feasibility
3 代码总流程
3.1 重复使用
3.2 转化到frenet坐标系
3.3 遍历每个路径边界点
3.4 判断是否pull-over或regular
3.5 优化路径
1 分段加加速度路径优化概览
1.1 输入,输出代码
//输入
PiecewiseJerkPathOptimizer::Process( const SpeedData& speed_data, const ReferenceLine& reference_line, const common::TrajectoryPoint& init_point, const bool path_reusable, PathData* const final_path_data)
//输出
OptimizePath函数得到最优的路径,信息包括opt_l,opt_dl,opt_ddl。在Process函数中最终结果保存到了task基类的变量reference_line_info_中。1.2 论文摘要
路径规划是自动驾驶汽车运动规划的关键组成部分。路径指定车辆将行驶的几何形状,因此,安全性和舒适性是至关重要的。对于城市驾驶场景,自动驾驶汽车需要能够在杂乱无章的环境中导航,例如,道路部分地被许多车辆/障碍物挡住。如何去生成一个运动学可行、平滑的、并且能够在复杂环境中避障的路径,这是路径规划中极具挑战的问题。在这篇论文中,我们提出了一个能生成最优路径的新颖的二次规划方法,这是以一定分辨率来完全避障的方法。
2 优化过程的详细数学理论
2.1 Smooth Driving Guide Line Generation
由于 Guide Line 是笛卡尔坐标系与frenet坐标系之前的桥梁,那么参考线的平滑性将严重影响路径的质量。同时由于用一些离散的点列去描述参考线,使得参考线的深层次几何信息丢失,比如曲率等,于是论文提出了基于优化的平滑算法。
目标函数:曲率小并且平滑的路径不仅有助于减少路径跟踪中的不稳定性或过冲,同时也增强了舒适性与驾驶体验。因此,参考线曲率和其变化率在优化中受到惩罚。对于城市驾驶场景,baidu Apollo鼓励车辆尽量保持在车道上。因此,参考线期望靠近车道的中心。并且我们还希望参考线不会因为我们的优化而变得过长。
约束条件:车辆具有最小转弯半径,我们在目标函数中希望路径曲率小,但在约束条件中不得不加入近似曲率要小于最小转弯半径对应的曲率这样的条件,这样一个硬约束才能保证车辆沿着比最小转弯半径大的弧运动
2.2 Path Planning in a Frenet Frame
将描述车辆状态量的六个变量通过转化到frenet坐标系下,变成横纵向解耦的六个变量,若不了解frenet坐标系,请参考【自动驾驶轨迹规划之Frenet坐标系】_无意2121的博客-CSDN博客_frenet坐标系
2.3 Path Boundary Decision and Computation
2.4 Path Optimization
(1)避障,满足路径边界的硬约束即可
(2)靠近车道的中心
(3)减少横向变化率
(4)与障碍物之间保持距离
具体目标函数和硬约束如下
但是上面的公式是针对于连续函数的,实际应用中我们仍旧需延续之前离散点的思路,对纵向距离进行等间隔采样
横向距离对纵向距离的一阶二阶导数就是优化问题的决策变量,三阶导数也就是jerk是恒定的,并可以由二阶导数计算得到
其实这就像是对很多离散点进行加加速度恒定的插值,这种分段插值,往往还需要在插值点上平滑过渡,所以等式约束就可以如下建立
于是优化问题就转化为如下形式
2.5 Variable Boundary Estimation for Kinematic Feasibility
由于在frenet坐标系下,我们难以判断这条轨迹在笛卡尔坐标系下是否运动学可行,因此我们只能把frenet坐标系转化回笛卡尔坐标系去判断。判断运动学可行性的最关键因素就是曲率及其变化率,下面就是两个坐标系之间曲率的转化公式
由于上述公式过于复杂,我们进行适当简化,并在原来的优化上加入新的约束条件
下图则验证了算法的有效性
3 代码总流程
3.1 重复使用
common::Status PiecewiseJerkPathOptimizer::Process(
const SpeedData& speed_data, const ReferenceLine& reference_line,
const common::TrajectoryPoint& init_point, const bool path_reusable,
PathData* const final_path_data) {
// 跳过piecewise_jerk_path_optimizer 如果路径重复使用
if (FLAGS_enable_skip_path_tasks && path_reusable) {
return Status::OK();
}
... ...3.2 转化到frenet坐标系
... ...
const auto init_frenet_state =
reference_line.ToFrenetFrame(planning_start_point);
// 为lane-change选择lane_change_path_config
// 否则, 选择default_path_config
const auto& config = reference_line_info_->IsChangeLanePath()
? config_.piecewise_jerk_path_optimizer_config()
.lane_change_path_config()
: config_.piecewise_jerk_path_optimizer_config()
.default_path_config();
... ...3.3 遍历每个路径边界点
... ...
const auto& path_boundaries =
reference_line_info_->GetCandidatePathBoundaries();
ADEBUG << "There are " << path_boundaries.size() << " path boundaries.";
const auto& reference_path_data = reference_line_info_->path_data();
std::vector candidate_path_data;
// 遍历每个路径
for (const auto& path_boundary : path_boundaries) {
size_t path_boundary_size = path_boundary.boundary().size();
... ... 3.4 判断是否pull-over或regular
... ...
if (!FLAGS_enable_force_pull_over_open_space_parking_test) {
// pull over场景
const auto& pull_over_status =
injector_->planning_context()->planning_status().pull_over();
if (pull_over_status.has_position() &&
pull_over_status.position().has_x() &&
pull_over_status.position().has_y() &&
path_boundary.label().find("pullover") != std::string::npos) {
common::SLPoint pull_over_sl;
reference_line.XYToSL(pull_over_status.position(), &pull_over_sl);
end_state[0] = pull_over_sl.l();
}
}
if (path_boundary.label().find("regular") != std::string::npos &&
reference_path_data.is_valid_path_reference()) {
ADEBUG << "path label is: " << path_boundary.label();
// 当参考路径就位
for (size_t i = 0; i < path_reference_size; ++i) {
common::SLPoint path_reference_sl;
reference_line.XYToSL(
common::util::PointFactory::ToPointENU(
reference_path_data.path_reference().at(i).x(),
reference_path_data.path_reference().at(i).y()),
&path_reference_sl);
path_reference_l[i] = path_reference_sl.l();
}
end_state[0] = path_reference_l.back();
path_data.set_is_optimized_towards_trajectory_reference(true);
is_valid_path_reference = true;
}
... ...3.5 优化路径
... ...
// 设置参数
const auto& veh_param =
common::VehicleConfigHelper::GetConfig().vehicle_param();
const double lat_acc_bound =
std::tan(veh_param.max_steer_angle() / veh_param.steer_ratio()) /
veh_param.wheel_base();
std::vector> ddl_bounds;
for (size_t i = 0; i < path_boundary_size; ++i) {
double s = static_cast(i) * path_boundary.delta_s() +
path_boundary.start_s();
double kappa = reference_line.GetNearestReferencePoint(s).kappa();
ddl_bounds.emplace_back(-lat_acc_bound - kappa, lat_acc_bound - kappa);
}
// 优化算法
bool res_opt = OptimizePath(
init_frenet_state.second, end_state, std::move(path_reference_l),
path_reference_size, path_boundary.delta_s(), is_valid_path_reference,
path_boundary.boundary(), ddl_bounds, w, max_iter, &opt_l, &opt_dl,
&opt_ddl);
... ... -
如果成功将值保存到candidate_path_data
... ...
if (res_opt) {
for (size_t i = 0; i < path_boundary_size; i += 4) {
ADEBUG << "for s[" << static_cast(i) * path_boundary.delta_s()
<< "], l = " << opt_l[i] << ", dl = " << opt_dl[i];
}
auto frenet_frame_path =
ToPiecewiseJerkPath(opt_l, opt_dl, opt_ddl, path_boundary.delta_s(),
path_boundary.start_s());
path_data.SetReferenceLine(&reference_line);
path_data.SetFrenetPath(std::move(frenet_frame_path));
if (FLAGS_use_front_axe_center_in_path_planning) {
auto discretized_path = DiscretizedPath(
ConvertPathPointRefFromFrontAxeToRearAxe(path_data));
path_data.SetDiscretizedPath(discretized_path);
}
path_data.set_path_label(path_boundary.label());
path_data.set_blocking_obstacle_id(path_boundary.blocking_obstacle_id());
candidate_path_data.push_back(std::move(path_data));
}
... ... -
失败则返回错误码,成功则保存路径点
... ...
if (candidate_path_data.empty()) {
return Status(ErrorCode::PLANNING_ERROR,
"Path Optimizer failed to generate path");
}
reference_line_info_->SetCandidatePathData(std::move(candidate_path_data));
return Status::OK();
... ...本文参考分段加加速度路径优化 — Apollo Auto 0.0.1 文档 (daobook.github.io)
《Optimal Vehicle Path Planning Using Quadratic Optimization for Baidu Apollo Open Platform》