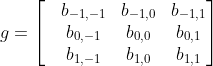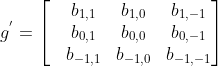浅谈卷积及其变种

首先，我们需要了解的是，何为卷积，何为卷积运算。

对卷积这个名词的理解：所谓两个函数的卷积，本质上就是先将一个函数翻转，然后进行滑动叠加，叠加指的是对两个函数的乘积求积分，在离散情况下就是加权求和。

对于图片来说，卷积的作用就是从线性不可分的图片里抽取出线性可分表示，那么线性可分表示也就是我们常说的特征。（因为博主研究方向和图像有关，这里就不展开介绍文本以及其他的了）类似地，卷积神经网络通过卷积在训练期间使用自动学习权重的函数来提取特征。所有这些提取出来的特征，之后会被组合在一起做出决策。

一张图像，可以看作一个由像素值组成的矩阵，如图：

 假设有一个3×3大小的卷积核，如下图：

 图像的卷积：取原始图像（u,v）处的矩阵，通过和卷积核的卷积运算，得到一个新的矩阵，新的矩阵（u,v）处的值就是原始图像（u,v）处的卷积。

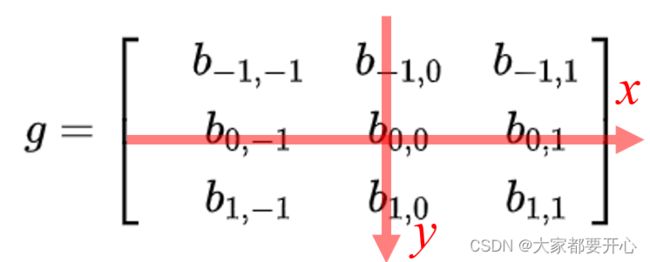
首先我们在原始图像矩阵中取出（u,v）处的矩阵：

 

先后沿着x，y轴翻转 （在这里特别注意：在深度学习中，卷积神经网络的卷积操作是不需要翻转的），可得到：

 最后计算内积得到：

 

信号处理中，卷积被定义为：一个函数经过翻转和移动后与另一个函数的乘积的积分。在深度学习中，卷积中的过滤函数是不经过翻转的。故此，深度学习中的卷积本质上就是信号/图像处理中的互相关（cross-correlation）。

卷积的优点：权重共享（weights sharing）和平移不变性（translation invariant），可以考虑像素空间的关系。

2D、3D卷积省略了，主要来讲一下听起来“高大上”的卷积变种。

首先提一下 1 x 1 卷积，下面H是height，W是width，D是depth

在一个维度为 H x W x D 的输入层上的操作方式。经过大小为 1 x 1 x D 的过滤器的 1 x 1 卷积，输出通道的维度为 H x W x 1。如果我们执行 N 次这样的 1 x 1 卷积，然后将这些结果结合起来，我们能得到一个维度为 H x W x N 的输出层。我们通常拿来降维。

空间可分离卷积

可分离卷积就是把一个原本3 x 3的卷积核分离为一个3 x 1的卷积核和一个1 x 3的卷积核。

比起卷积，空间可分离卷积要执行的矩阵乘法运算也更少。假设我们现在在 m x m 卷积核、卷积步长=1 、填充=0 的 N x N 图像上做卷积。传统的卷积需要进行 (N-2) x (N-2) x m x m 次乘法运算，而空间可分离卷积只需要进行 N x (N-2) x m + (N-2) x (N-2) x m = (2N-2) x (N-2) x m 次乘法运算。空间可分离卷积与标准的卷积的计算成本之比为：2/m + 2/m(N-2)

深度可分离卷积

对应3D卷积，不是博主的研究领域，就不细说了。

分组卷积

参考AlexNet，分组卷积（Group Convolution）顾名思义，在对特征图进行卷积的时候，首先对特征图分组再卷积。

减少参数量，分组卷积可以看做是对原来的特征图进行了一个dropout，有正则的效果。

扩张卷积

dilation rate（膨胀系数、扩张速率）kernel size（卷积核大小）

new_kernel size = dilation rate * (kernel size - 1) + 1

扩张卷积引入另一个卷积层的参数被称为扩张率。这定义了内核中值之间的间距。扩张速率为2的3x3内核将具有与5x5内核相同的视野，而只使用9个参数。 想象一下，使用5x5内核并删除每个间隔的行和列。计算机能以相同的计算成本，提供更大的感受野。扩张卷积在实时分割领域特别受欢迎。 在需要更大的观察范围，且无法承受多个卷积或更大的内核，可以才用它。

反卷积

反卷积的作用 反卷积，顾名思义是卷积操作的逆向操作。 为了方便理解，假设卷积前为图片，卷积后为图片的特征。 卷积，输入图片，输出图片的特征，理论依据是统计不变性中的平移不变性（translation invariance），起到降维的作用。

小tip：生成对抗网络中从特征生成图像。

Octave Convolution

octconv就如同CNN的压缩器，代替传统的卷积，能在提升效果的同时，节约计算资源。比如说一个经典的图像识别算法，换掉其中的传统卷积，在ImageNet上的识别精度能获得1.2%的提升，同时，只需要82%的算力和91%的存储空间。如果对精度没有那么高的要求，和原来持平满足了的话，只需要一半的浮点运算能力就够了。

核心原理就是利用空间尺度化理论将图像高频低频部分分开，下采样低频部分，可以大大降低参数量，并且可以完美的嵌入到神经网络中。降低了低频信息的冗余。

CNNs生成的特征图在空间维度上也存在大量冗余，每个位置独立存储自己的特征描述符，忽略了可以一起存储和处理的相邻位置之间的公共信息

通过octave convolution 减少空间冗余度。不仅仅自然图像，在卷积层输出的特征图中也存在高低频分量。而低频分量的存在是冗余的，在编码过程可以节省。

在图像中，一般包含了低频信息（全局结构）和高频信息（细节）。CONV输出的feature map也相当于不同频率信息的混合。

在论文中通过频率来分解混合的feature map，设计Octave Convolution，以较低的空间分辨率存储和处理空间变化“较慢”的特征图，从而降低内存和计算成本。

同时CctConv是一种单一、通用、即插即用的卷积单元，可以直接代替（普通）卷积，而无需对网络结构进行任何调整。它也是正交和互补的方法，建议更好的拓扑结构或减少信道冗余，如分组或深度卷积。通过简单将OctConv代替传统的卷积层，可以提升分类任务的精确度，同时可以减少存储空间与计算量。

在自然图像中，信息以不同的频率传递，其中较高的频率通常用精细的细节编码，较低的频率通常用全局结构编码。同样，卷积层的输出特征图也可以看作是不同频率下信息的混合。