监督学习 | SVM 之非线性支持向量机原理

相关文章：

机器学习 | 目录

机器学习 | 网络搜索及可视化

监督学习 | SVM 之线性支持向量机原理

监督学习 | SVM 之支持向量机Sklearn实现

1. 非线性支持向量机

对解线性分类问题，线性分类支持向量机是一种非常有效的方法。但是，有时分类问题是非线性的，这时可以使用非线性支持向量机（non-linear support vector machine）。

非线性分类问题是指通过利用非线性模型才能很好地进行分类的问题。如下图所示，这是一个分类问题，无法用直线（线性模型）将正负实例正确分开，但可以用一条椭圆（非线性模型）将它们正确分开。^[1]

图1 非线性分类问题与核技巧示例

再看一个“异或”问题，同样也不是线性可分的：

图2 异或问题与非线性映射

对这样的问题，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。如图 2 所示，若将原始的二维空间映射到一个合适的三维空间，就可以找到一个合适的划分超平面。当原始空间是有限维（即属性数是有限的），那么一定存在一个高维特征空间使样本可分。

令 $\varphi (x)$ 表示将 $x$ 映射后的特征向量，于是，在特征空间中划分超平面模型可表示为：

$$f(x)=w^T\varphi (x)+b\text{\hspace{1em}(1)}$$

线性可分支持向量机的原始问题变为：

$$\begin{array}{ll}\underset{w,b}{\min }& \frac{1}{2}\Vert w{\Vert }^2\\ \text{ s.t. }& y_i\left(w^T\varphi (x_i)+b\right)-1⩾0,i=1,2,\cdots ,N\end{array}\text{\hspace{1em}(2)}$$

其对偶问题为：

$$\begin{array}{ll}\underset{\alpha }{\max }& {\sum }_{i=1}^N{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi (x_i{)}^T\varphi (x_j)\\ \text{ s.t. }& {\sum }_{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i⩾0,i=1,2,\cdots ,N\end{array}\text{\hspace{1em}(3)}$$

1.1 核技巧

求解 (2) 涉及到计算 $\varphi (x_i{)}^T\varphi (x_j)$，这是样本 $x_i$ 与 $x_j$ 映射到特征空间之后的内积。由于特征空间维数可能很高，设置可能是无穷维，因此直接计算 $\varphi (x_i{)}^T\varphi (x_j)$ 通常是困难的。为了避开这个障碍，可以设想这样一个函数：

$$k(x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)\text{\hspace{1em}(4)}$$

核技巧：$x_i$ 与 $x_j$ 在特征空间的内积等于它们在原始样本空间中通过函数 $k(\cdot ,\cdot )$ 计算的结果，于是 (3)可以重写为：

$$\begin{array}{ll}\underset{\alpha }{\max }& {\sum }_{i=1}^N{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}k(\cdot ,\cdot )\\ \text{ s.t. }& {\sum }_{i=1}^N{\alpha }_i{y}_i=0\\ & {\alpha }_i⩾0,i=1,2,\cdots ,N\end{array}\text{\hspace{1em}(5)}$$

求解后即可得到：

$$\begin{array}{ll}f(x)& =w^T\varphi (x)+b\\ & ={\sum }_{i=1}^N{\alpha }_i{y}_i\varphi (x_i{)}^T\varphi (x)+b\\ & ={\sum }_{i=1}^N{\alpha }_i{y}_{i}k(x,x_i)+b\end{array}\text{\hspace{1em}(6)}$$

这里的函数 $k(\cdot ,\cdot )$ 就是“核函数”（kernel function）。上式显示出模型最优解可以通过训练样本的核函数展开，这一展开式又称为支持向量展式（support vector expansion）。

1.2 核函数

定理（核函数）：令 $X$ 为输入空间，$k(\cdot ,\cdot )$ 是定义在 $X\times X$ 上的对称函数，则 $k$ 是核函数当且仅当对于任意数据 $D=\{x_1,x_2,\cdots x_m\}$，“核矩阵”（kernel matrix）$K$ 总是半正定的：^[2]

$$\mathbf{K}=\left[\begin{array}{ccccc}\kappa \left({\mathbf{x}}_1,{\mathbf{x}}_1\right)& \cdots & \kappa \left({\mathbf{x}}_1,{\mathbf{x}}_j\right)& \cdots & \kappa \left({\mathbf{x}}_1,{\mathbf{x}}_m\right)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_1\right)& \cdots & \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)& \cdots & \kappa \left({\mathbf{x}}_i,{\mathbf{x}}_m\right)\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ \kappa \left({\mathbf{x}}_m,{\mathbf{x}}_1\right)& \cdots & \kappa \left({\mathbf{x}}_m,{\mathbf{x}}_j\right)& \cdots & \kappa \left({\mathbf{x}}_m,{\mathbf{x}}_m\right)\end{array}\right]\text{\hspace{1em}(7)}$$

这个定理表明，只要一个对称函数所对应的核矩阵半正定，它就能作为核函数使用。事实上，对于一个半正定核矩阵，总能找到一个与之对应的映射 $\varphi$ 。换言之，任何一个核函数都隐式地定义了一个称为“再生核希尔伯特空间”（RKHS, Reproducing Kernel Hilbert Space）的特征空间。

1.2.1 核函数选择

通过前面讨论我们知道，我们希望样本在特征空间内线性可分，因此特征空间的好坏对支持向量机的性能直观重要。需要注意的是，在不知道特征映射的形式时，我们并不知道什么样的核函数时合适的，而核函数也仅是隐式地定义了这个特征空间。于是，“核函数选择”称为支持向量机的最大变数。若核函数选择不合适，则意味着将样本映射到了一个不合适的特征空间，很可能导致性能不佳。

表1 常用核函数

对文本数据通常采用线性核；情况不明时可先尝试高斯核（RBF 核）

此外，还可以通过函数组合得到，例如：

• 若 $k_1$ 和 $k_1$ 为核函数，则对于任意正数 ${\gamma }_1,{\gamma }_2$，其线性组合：

$${\gamma }_1{k}_1+{\gamma }_2{k}_2\text{\hspace{1em}(8)}$$

也是核函数；

• 若 $k_1$ 和 $k_1$ 为核函数，则核函数的直积：

$$k_1\otimes k_2(x,z)=k_1(x,z)k_2(x,z)\text{\hspace{1em}(9)}$$

也是核函数；

• 若 $k_1$ 为核函数，则对于任意函数 $g(x)$：

$$k(x,z)=g(x)k_1(x,z)g(z)\text{\hspace{1em}(10)}$$

也是核函数。

1.2.2 RBF 函数

首先来看一个例子，假设我们要将一组直线上的数据进行分类，但由于它们是非线性的，因此需要利用核函数将数据变换为线性可分的数据。

图3 非线性数据

我们通过一条曲线将直线上的数据投射到一个平面上，可以看见，所有的正实例都被投射到了曲线的顶端，而所有的负实例都被投射到了曲线的低端，因此这时我们就可以利用线性可分支持向量机找出分类超平面。

图4 高斯核函数变换后的线性可分数据

那么这条曲线是怎么构造出来的呢，这里就要介绍一个函数：径向基函数（RBF Radial Basis Function）。

所谓径向基函数，就是某种沿径向对称的标量函数。通常定义为空间中任一点 $x$ 到某中心 $x_c$ 之间欧式距离的单调函数，可以记为 $k(x,x_c)$，其作用往往是局部的，即当 $x$ 原理 $x_c$ 时函数取值很小。

最常用的径向基函数是高斯径向基函数：

$$k(x,x_c)=exp(-\frac{\Vert x-x_c{\Vert }^2}{2{\sigma }^2})\text{\hspace{1em}(11)}$$

当我们使用高斯径向基函数作为核函数时，就称之为高斯核函数。

它的图像与高斯分布 $y=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$ 相似，在高斯分布中，其分布被参数 $\sigma$ 和 $\mu$ 唯一确定，当 $\sigma$ 越大时，图像越矮胖；当 $\sigma$ 越小时，图像越高瘦。

图5 正态分布图

类似地，我们在高斯径向基函数中使用 gamma 参数来决定图像的高瘦或矮胖：

$$\gamma =\frac{1}{2{\sigma }^2}\text{\hspace{1em}(12)}$$

当 $\gamma$ 越大时，图像越高瘦；当 $\gamma$ 越小时，图像越矮瘦：

图6 参数 gamma 的大小对图像的影响

在高维数据中也相似：

图7 高维度下参数 gamma 的大小对图像的影响

此时超平面的截面即为分类数据的边界：

图8 参数 gamma 的大小对拟合程度的影响

当我们使用高斯核函数时，此时的非线性支持向量机则由参数 $\gamma$ 和惩罚参数 $C$ 所确定：

当 $\gamma$ 越大时，越有可能过拟合；当 $\gamma$ 越小时，越有可能欠拟合；

当 $C$ 越大时，对误分类的惩罚越大；当 $C$ 越小时，对误分类的惩罚越小。

由于 SVM 模型没有先验信息，所以可以使用网络搜索来确定参数大小。

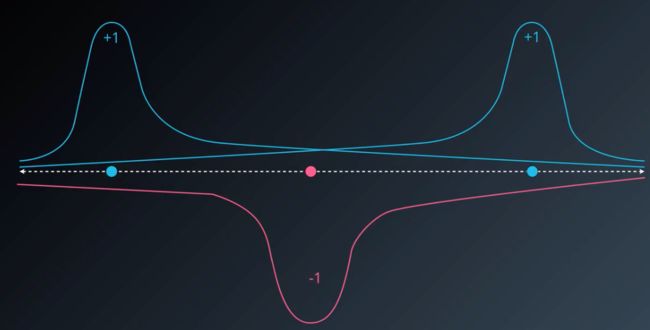
现在我们可以回答开头的例子中曲线时怎么拟合出来的了，我们通过在每一个数据点上使用一个高斯核函数，可以将数据分为两类，接着用一个连续平滑的曲线将这些图形连接起来，就得到了曲线：

图8 利用高斯核函数将数据线性化 图9 数据投射的曲线

参考资料

[1] 李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012: 115-116.

[2] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 127-129.