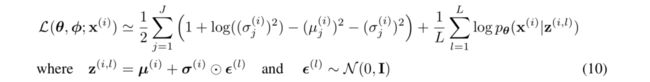CS285课程笔记（5.(1)）——从概率图角度理解强化学习（变分推断原理+VAE）

Lecture 18, 19 (2020版)这两节课的核心内容就是如何把强化学习问题（又可以称为最优控制问题）转化为一个基于概率图模型的推断问题，这里的推断又可以进一步细分为精确推断（Exact Inference）和近似推断 (Approximate Inference)。本文先总结lectrue 18，即变分推断与变分推断自编码器的基础知识。

一、变分推断与变分自编码器（Variational Inference and Variational Autoencoder）

1. 概率隐变量模型（Probabilistic Latent Variable Models）

什么是隐变量模型

在介绍隐变量模型之前，先回顾一下概率模型或条件概率（$p(x),p(y|x)$）的概念。所谓概率模型就是在给定一些输入数据之后，计算其可能的概率分布，条件概率模型也类似。而隐变量概率模型适用于那些给定数据之间可能存在某种局部关系的场景，例如机器学习中的聚类方法。这种局部关系可以用另外一个变量的概率分布$p(z)$描述，例如下图中的$z$代表的是原始数据的类别，例如该变量描述的是数据类别，其满足最简单的均匀分布，这里假设有3类 $Z=(z_1,z_2,z_3)$，在给定类别$z_i$之后，原始数据$x$的概率分布为：$p(x|z_i)$，从图中可以看出他们满足二维高斯分布，那么整个数据的概率分布由全概率公式就可以写成：$p(x)={\sum }_1^{3}p(x|z_i)p(z_i)=p(x|z_1)p(z_1)+p(x|z_2)p(z_2)+p(x|z_3)p(z_3)$。通过上文可以看出，使用隐变量模型的一个好处就是可以用简单的模型来表示复杂的概率分布。

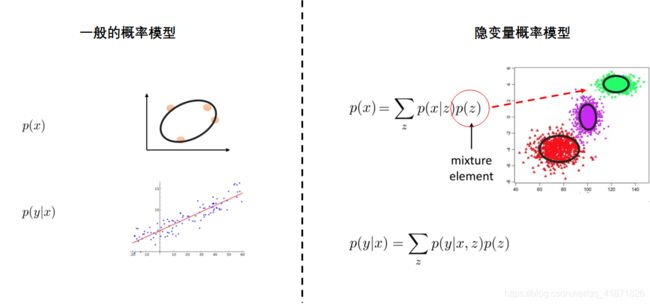
以上例子是假设隐变量为离散情况，隐变量模型也可以用于连续隐变量情况，公式可以写成：
$$p(x)=\int p(x|z)p(z)dz$$
这里的$p(x|z)$，$p(z)$可以较为简单的概率分布，例如在下图中，这里的$p(x|z)$是多元高斯分布，其均值与方差通过神经网络的输出得到，而$p(z)$是一个简单的一维高斯分布。

RL问题中的隐变量模型
在之前的Lecture中，尤其是model based RL中的Latent variable models中提到，假设环境是Partially observable的情况下，那么隐变量模型可以是emission probability, $p(o_t|s_t)$或者是latent reward，$r(s_t,a_t)$等。

如何训练隐变量模型

在没有隐变量模型，即用一般的机器学习算法训练生成模型的过程中使用的是最大似然函数作为损失函，如果这时候将含隐变量模型的公式带入可以得到新的损失函数，但是这个损失函数是很难求解的（completely intractable），如下图所示：

那么接下来的问题就是如何让新的目标函数变得可以求解呢？这里的积分项中$z$由于是隐变量所以它是未知的，需要对它进行一些数学上的代数变形，即只有先得到与$z$相关的一些分布之后，才能得到整体$x$的分布。与$z$相关的分布无非就是先验概率$p(z)$和后验概率$p(z|x_i)$，可以将后验概率其解释为给定数据$x_i$之后，这些数据所属类别是什么。 这里先猜测能否将积分项替换为与期望有关的表达式，即对后验概率$p(z|x_i)$求$\log p_{\theta }(x_i,z)$的期望（我认为不是如lectrue所说先猜想，应该是通过后续ELBO，Evidence Lower Bound相关概念的引入推导出来的，ELBO见第二节）。所以上述损失函数的更新就变成了：
$$\theta \leftarrow \underset{\theta }{\mathrm{argmax}}\frac{1}{N}\sum _i{E}_{z\sim p(z|x_i)}[\log p_{\theta }(x_i,z)]$$
接下来的问题就是如何计算后验概率的问题。

2. 变分推断基本原理

The Variational Approximation

首先，上文对使用后验概率$p(z|x_i)$这一假设其实是源于对$\log p_{\theta }(x_i)$的bound和KL散度。公式推导中先省略$\theta$，过程如下：
$$\begin{gathered} \log p(x_i)=\log {\int }_{z}p(x_i|z)p(z)dz=\log {\int }_{z}p(x_i|z)p(z)\frac{q_i(z)}{q_i(z)}dz \\ =\log E_{z\sim q_i(z)}\left[\frac{p(x_i|z)p(z)}{q_i(z)}\right]\ge E_{z\sim q_i(z)}\left[\log \frac{p(x_i|z)p(z)}{q_i(z)}\right]=E_{z\sim q_i(z)}[\log p(x_i|z)+\log p(z)]+\mathcal{H}(q_i) \end{gathered}$$
上式中用到了一个不等式关系：$\log E[\cdot ]\ge E[\log (\cdot )]$从上式可以看出（可以从log函数的图像中看出，这里的$E[\log (\cdot )]$相当于函数值的均值，$\log (E[\cdot ])$相当于均值的函数值），最大似然求解就是要最大化这个Bound，因为从上式可以看出这里只需逐步最大化Bound即可达到最大化似然函数的目的。这里将这个bound记为${\mathcal{L}}_i(p,q_i)$，在直观理解这个Bound之前，先来验证一下上文中的假设使用$p(z|x_i)$是否合理，这里是通过推导$q_i(z)$与$p(z|x_i)$之间的KL散度进行验证，这里的$q_i(z)$是对后验概率$p(z|x_i)$的估计，根据KL散度的定义如下图：

这里的${\mathcal{L}}_i(p,q_i)=E_{z\sim q_i(z)}[\log p(x_i,z)]+\mathcal{H}(q_i)=E_{z\sim q_i(z)}[\log p(x_i|z)+\log p(z)]+\mathcal{H}(q_i)$本质上就是上文中的参数更新式子中的$\theta \leftarrow \underset{\theta }{\mathrm{argmax}}\frac{1}{N}{\sum }_i{E}_{z\sim p(z|x_i)}[\log p_{\theta }(x_i,z)]$，只不过这里使用的是在每个样本点上估计出的概率分布$q_i(z)$，并且通过$\log p(x_i)\ge {\mathcal{L}}_i(p,q_i)$可以看出，只要最大化${\mathcal{L}}_i(p,q_i)$即可最大化$\log p(x_i)$。

那么以上通过最大化函数${\mathcal{L}}_i(p,q_i)=E_{z\sim q_i(z)}[\log p_{\theta }(x_i|z)+\log p(z)]+\mathcal{H}(q_i)$来等效达到最大化似然函数的效果，其直观解释是什么呢？有以下的两部分解释，首先由熵的定义可知，变量的概率分布越随机，其熵越大。式子中的第一部分是寻找到概率分布$q_i(z)$能够使$p_{\theta }(x_i,z)$最大，第二项由于是最大化$q_i(z)$的熵，则其直观解释就是将其概率分布尽可能变宽，直观上的图形解释如下：

除了最大化${\mathcal{L}}_i(p,q_i)=E_{z\sim q_i(z)}[\log p_{\theta }(x_i|z)+\log p(z)]+\mathcal{H}(q_i)$之外，还应该在用$q_i(z)$估计概率分布$p(z|x_i)$的过程中让两者的KL散度尽可能接近，这样才能保证最大化函数${\mathcal{L}}_i(p,q_i)$的同时又最大化了$\log p(x_i)$。

基本训练过程及存在的问题

变分推断最基本的算法过程
变分推断的基本过程就是把上文的$E[\log p_{\theta }(x_i)]$换成目标函数${\mathcal{L}}_i(p,q_i)$。最大化目标函数分为两步，首先先对对每个数据点$x_i$，计算目标函数的梯度${\nabla }_{\theta }{\mathcal{L}}_i(p,q_i)\approx {\nabla }_{\theta }\log p_{\theta }(x_i|z)$，用梯度上升的方法最大化该函数；第二步是用$q_i$对目标函数进行最大化，这里可以假设选取的近似概率分布$q_i(z)$为参数化的高斯分布（参数分别为均值和方差，这里PPT中的高斯分布表达式并不严谨，应该是 $\mathcal{N}({\mu }^{(i)},{\sigma }^{2(i)}I)$）并以对参数求梯度的方式最大化目标函数。

存在的问题
从上文的变分推断过程可以看出其存在参数空间随着数据的增加不断变大的问题。由于这里要对每个数据点 $x_i$ 最大化目标函数${\mathcal{L}}_i(p_{\theta },q_i)$，所需参数为$|\theta |+(|{\mu }_i|+|{\sigma }_i|)\times N$。那么如何减小所需参数数量呢？一种方式是用两个神经网络来估计相对应的$p_{\theta }(x|z)$和$q_{\varphi }(z|x)$概率分布。

3. Amortized Variational Inference (AVI)

AVI的基本框架

AVI的基本思想就是用两个网络近似对应的两个分布，以解决参数空间爆炸的问题，其基本流程图如下：

问题依然在于如何求解目标函数${\mathcal{L}}_i(p,q_i)$对参数$\varphi$的梯度${\nabla }_{\varphi }\mathcal{L}$。回忆上文的目标函数展开形式：${\mathcal{L}}_i=E_{z\sim q_{\varphi }(z|x_i)}[\log p_{\theta }(x_i|z)+\log p(z)]+\mathcal{H}(q_{\varphi }(z|x_i))$，在对参数$\varphi$求导，观察一下式子中的第一项，可以看出它与Policy gradient的表达式是类似的（$J=E_{\tau \sim p_{\theta }(\tau )}[\sum r({\text{s}}_t,{\text{a}}_t)]$，期望运算括号里的变量与下标中带参数的概率分布无关），可以将其简写成：$J(\varphi )=E_{z\sim q_{\varphi }(z|x_i)}[r(x_i,z)]$，这里的$r(x_i,z)=\log p_{\theta }(x_i|z)+\log p(z)$，所以可以由策略梯度定理，并在Monte Carlo采样的基础上得到其梯度公式的近似表达式：
$$\nabla J(\varphi )\approx \frac{1}{M}\sum _j{\nabla }_{\varphi }\log q_{\varphi }(z_j|x_i)r(x_i,z_j)=\frac{1}{M}\sum _j{\nabla }_{\varphi }\log q_{\varphi }(z_j|x_i)(\log p_{\theta }(x_i|z)+\log p(z))$$

由于上式是用策略梯度定理导出的，那么它也存在与策略梯度一样的问题，就是方差比较大，导致策略梯度的值波动较大。造成其方差较大的原因在于采样是从$q_{\varphi }(z|x_i)$中抽样的，其是一个未知的概率分布，所以尽管使用策略梯度是合理的，但这不是最优的求解方法。更好的方法是使用reparameterization trick。

The Reparameterization Trick

由于概率分布$q_{\varphi }(z|x_i)$是未知的，所以考虑能否将其换成一个已知的概率分布来减小方差。由于上文假设$q_{\varphi }(z|x_i)$是高斯分布$\mathcal{N}({\mu }_{\varphi }(x),{\sigma }_{\varphi }(x))$，即$z\sim \mathcal{N}({\mu }_{\varphi }(x),{\sigma }_{\varphi }(x))$所以这里进行以下变形，令：$\frac{z-{\mu }_{\varphi }(x)}{{\sigma }_{\varphi }(x)}\sim (ϵ\sim \mathcal{N}(0,1))$，即$z={\mu }_{\varphi }(x)+ϵ{\sigma }_{\varphi }(x)$，并将其带入上文中的损失函数中，即
$$J(\varphi )=E_{z\sim q_{\varphi }(z|x_i)}[r(x_i,z)]=E_{z\sim \mathcal{N}(0,1)}[r(x_i,{\mu }_{\varphi }(x)+ϵ{\sigma }_{\varphi }(x))]$$
上述损失函数的梯度是比较好得到的，对其梯度进行估算的流程如下：

先从$\mathcal{N}(0,1)$中采样数据点${ϵ}_1,\dots ,{ϵ}_M$，之后直接用自动求导包对其求导即可。

用该方法再对上文中的目标函数${\mathcal{L}}_i=E_{z\sim q_{\varphi }(z|x_i)}[\log p_{\theta }(x_i|z)+\log p(z)]+\mathcal{H}(q_{\varphi }(z|x_i))=E_{z\sim q_{\varphi }(z|x_i)}[\log p_{\theta }(x_i|z)]+(E_{z\sim q_{\varphi }(z|x_i)}[\log p(z)]-E_{z\sim q_{\varphi }(z|x_i)}[\log q_{\varphi }(z|x_i)])=E_{z\sim q_{\varphi }(z|x_i)}[\log p_{\theta }(x_i|z)]-D_{KL}(q_{\varphi }(z|x_i)||p(z))$进行变形，可以得到：
$$\begin{gathered} E_{z\sim q_{\varphi }(z|x_i)}[\log p_{\theta }(x_i|z)]-D_{KL}(q_{\varphi }(z|x_i)||p(z)) \\ =E_{z\sim \mathcal{N}(0,1)}[\log p_{\theta }(x_i|{\mu }_{\varphi }(x_i)+ϵ{\sigma }_{\varphi }(x_i))]-D_{KL}(q_{\varphi }(z|x_i)||p(z)) \\ \approx \log p_{\theta }(x_i|{\mu }_{\varphi }(x_i)+ϵ{\sigma }_{\varphi }(x_i))-D_{KL}(q_{\varphi }(z|x_i)||p(z)) \end{gathered}$$

整个算法流程如下：第一个神经网络是$q_{\varphi }(z|x_i)$，经过reparameterization trick之后是$q_{\varphi }({\mu }_{\varphi }(x_i)+ϵ{\sigma }_{\varphi }(x_i)|x_i)$，第二个神经网络是$p_{\theta }(x_i|z)$。

Reparameterization Trick与Policy Gradient优劣对比

以上的reparameterization trick和直接借用policy gradient的方法各有利弊。Policy gradient的优点是它可以既可以处理离散隐变量也可以处理连续隐变量，但它的缺点就是高方差，波动较大，需要非常多的数据量。而reparameterization trick实现起来非常容易，而且它的方差比较小，但缺点就是只能处理连续隐变量，因为这里要对函数$r(\cdot )$求导，其必须是连续可微的。

4. 变分自编码器 (High-level Idea of VAE)

VAE基本流程

变分推断的一个例子就是Variational Autoencoder，本节课也是介绍了该模型的high-level idea，没有详细具体介绍细节，基本的流程与上文的amortized variational inference类似，只不过encoder, decoder可以是更加复杂的网络，而且损失函数与其也不同，但同样也是两部分组成，一部分是reconstruction loss，另一部分是KL散度部分（由于$q_{\varphi }(z)$使用的是高斯分布，所以这里的KL散度可以展开来写，方便coding实现）。其与amortized VI不同，如下：

其原始形式就是：

这里的variational approximator是：

这里的均值和方差为encoder（MLP网络）的输出。

损失函数中的KL散度$D_{KL}(q_{\varphi }(\text{z})||p_{\theta }(\text{z}))$推导过程如下：

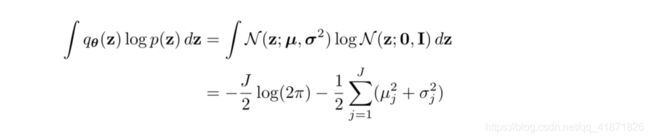
上文推导可能有些简略，这里引用这篇博文里的推导过程：

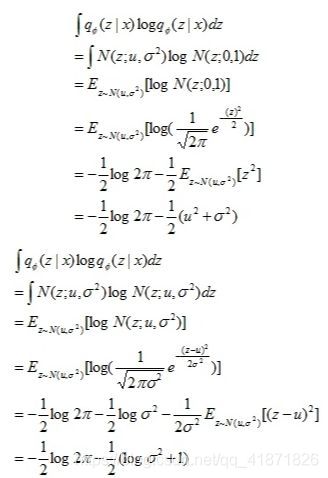
上述推导没有考虑隐变量的维度$J$，但这里都用到了高斯分布的二阶矩，这里假设$\text{X}\sim \mathcal{N}(\mu ,\Sigma )$，维数为$J$，那么多元变量$\text{X}$的pdf就是：
$$p(\text{X})=\frac{1}{(2\pi {)}^{\frac{J}{2}}|\Sigma {|}^{\frac{1}{2}}}\exp (-\frac{1}{2}(\text{X}-\mu ){\Sigma }^{-1}(\text{X}-\mu {)}^T)$$

其二阶矩为：
$$E_{\text{X}\sim N(\mu ,\Sigma )}[(\text{X}-\mu )(\text{X}-\mu {)}^T]=\Sigma$$
这里方便理解的话只用一维正态分布理解上述损失函数，这里随机变量用$Z$表示：
$$p(Z)=\frac{1}{(2\pi {\sigma }^2{)}^{\frac{1}{2}}}\exp (-\frac{1}{2{\sigma }^2}(Z-\mu {)}^2)$$
其二阶矩为：
$$E_{Z\sim N(\mu ,\Sigma )}[(Z-\mu {)}^2]=\int N(z;\mu ,\sigma )(Z-\mu {)}^{2}dZ={\sigma }^2$$
进行代数变形可得：
$$E_{Z\sim N(\mu ,\Sigma )}[Z^2-2Z\mu +{\mu }^2]=E_Z[Z^2]-2\mu E_Z[Z]+{\mu }^2=E_Z[Z^2]-{\mu }^2={\sigma }^2$$
所以
$$E_{Z\sim N(\mu ,\sigma )}[Z^2]={\mu }^2+{\sigma }^2$$

这里搬运一个tensorflow教程的VAE代码部分，使用的数据集时MNIST。

""" Variational Auto-Encoder Example.

Using a variational auto-encoder to generate digits images from noise.
MNIST handwritten digits are used as training examples.

References:
    - Auto-Encoding Variational Bayes The International Conference on Learning
    Representations (ICLR), Banff, 2014. D.P. Kingma, M. Welling
    - Understanding the difficulty of training deep feedforward neural networks.
    X Glorot, Y Bengio. Aistats 9, 249-256
    - Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. "Gradient-based
    learning applied to document recognition." Proceedings of the IEEE,
    86(11):2278-2324, November 1998.

Links:
    - [VAE Paper] https://arxiv.org/abs/1312.6114
    - [Xavier Glorot Init](www.cs.cmu.edu/~bhiksha/courses/deeplearning/Fall.../AISTATS2010_Glorot.pdf).
    - [MNIST Dataset] http://yann.lecun.com/exdb/mnist/

Author: Aymeric Damien
Project: https://github.com/aymericdamien/TensorFlow-Examples/
"""
from __future__ import division, print_function, absolute_import

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
import tensorflow as tf

# Import MNIST data
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)

# Parameters
learning_rate = 0.001
num_steps = 30000
batch_size = 64

# Network Parameters
image_dim = 784 # MNIST images are 28x28 pixels
hidden_dim = 512
latent_dim = 2

# A custom initialization (see Xavier Glorot init)
def glorot_init(shape):
    return tf.random_normal(shape=shape, stddev=1. / tf.sqrt(shape[0] / 2.))

# Variables
weights = {
    'encoder_h1': tf.Variable(glorot_init([image_dim, hidden_dim])),
    'z_mean': tf.Variable(glorot_init([hidden_dim, latent_dim])),
    'z_std': tf.Variable(glorot_init([hidden_dim, latent_dim])),
    'decoder_h1': tf.Variable(glorot_init([latent_dim, hidden_dim])),
    'decoder_out': tf.Variable(glorot_init([hidden_dim, image_dim]))
}
biases = {
    'encoder_b1': tf.Variable(glorot_init([hidden_dim])),
    'z_mean': tf.Variable(glorot_init([latent_dim])),
    'z_std': tf.Variable(glorot_init([latent_dim])),
    'decoder_b1': tf.Variable(glorot_init([hidden_dim])),
    'decoder_out': tf.Variable(glorot_init([image_dim]))
}

# Building the encoder
input_image = tf.placeholder(tf.float32, shape=[None, image_dim])
encoder = tf.matmul(input_image, weights['encoder_h1']) + biases['encoder_b1']
encoder = tf.nn.tanh(encoder)
z_mean = tf.matmul(encoder, weights['z_mean']) + biases['z_mean']
z_std = tf.matmul(encoder, weights['z_std']) + biases['z_std']

# Sampler: Normal (gaussian) random distribution
eps = tf.random_normal(tf.shape(z_std), dtype=tf.float32, mean=0., stddev=1.0,
                       name='epsilon')
z = z_mean + tf.exp(z_std / 2) * eps

# Building the decoder (with scope to re-use these layers later)
decoder = tf.matmul(z, weights['decoder_h1']) + biases['decoder_b1']
decoder = tf.nn.tanh(decoder)
decoder = tf.matmul(decoder, weights['decoder_out']) + biases['decoder_out']
decoder = tf.nn.sigmoid(decoder)


# Define VAE Loss
def vae_loss(x_reconstructed, x_true):
    # Reconstruction loss
    encode_decode_loss = x_true * tf.log(1e-10 + x_reconstructed) \
                         + (1 - x_true) * tf.log(1e-10 + 1 - x_reconstructed)
    encode_decode_loss = -tf.reduce_sum(encode_decode_loss, 1)
    # KL Divergence loss
    kl_div_loss = 1 + z_std - tf.square(z_mean) - tf.exp(z_std)
    kl_div_loss = -0.5 * tf.reduce_sum(kl_div_loss, 1)
    return tf.reduce_mean(encode_decode_loss + kl_div_loss)

loss_op = vae_loss(decoder, input_image)
optimizer = tf.train.RMSPropOptimizer(learning_rate=learning_rate)
train_op = optimizer.minimize(loss_op)

# Initialize the variables (i.e. assign their default value)
init = tf.global_variables_initializer()

# Start training
with tf.Session() as sess:

    # Run the initializer
    sess.run(init)

    for i in range(1, num_steps+1):
        # Prepare Data
        # Get the next batch of MNIST data (only images are needed, not labels)
        batch_x, _ = mnist.train.next_batch(batch_size)

        # Train
        feed_dict = {input_image: batch_x}
        _, l = sess.run([train_op, loss_op], feed_dict=feed_dict)
        if i % 1000 == 0 or i == 1:
            print('Step %i, Loss: %f' % (i, l))

    # Testing
    # Generator takes noise as input
    noise_input = tf.placeholder(tf.float32, shape=[None, latent_dim])
    # Rebuild the decoder to create image from noise
    decoder = tf.matmul(noise_input, weights['decoder_h1']) + biases['decoder_b1']
    decoder = tf.nn.tanh(decoder)
    decoder = tf.matmul(decoder, weights['decoder_out']) + biases['decoder_out']
    decoder = tf.nn.sigmoid(decoder)

    # Building a manifold of generated digits
    n = 20
    x_axis = np.linspace(-3, 3, n)
    y_axis = np.linspace(-3, 3, n)

    canvas = np.empty((28 * n, 28 * n))
    for i, yi in enumerate(x_axis):
        for j, xi in enumerate(y_axis):
            z_mu = np.array([[xi, yi]] * batch_size)
            x_mean = sess.run(decoder, feed_dict={noise_input: z_mu})
            canvas[(n - i - 1) * 28:(n - i) * 28, j * 28:(j + 1) * 28] = \
            x_mean[0].reshape(28, 28)

    plt.figure(figsize=(8, 10))
    Xi, Yi = np.meshgrid(x_axis, y_axis)
    plt.imshow(canvas, origin="upper", cmap="gray")
    plt.show()

Conditional VAE

条件VAE只是相较普通VAE多了一个变量y，没有本质区别，流程图如下：

其他与VAE有关的博文：

1. https://zhuanlan.zhihu.com/p/144649293
2. https://zhuanlan.zhihu.com/p/34998569
3. 多元高斯分布详细介绍